[Reinforcement Learning] Policy Gradient Methods

上一篇博文的内容整理了我们如何去近似价值函数或者是动作价值函数的方法：
\[
V_{\theta}(s)\approx V^{\pi}(s) \\
Q_{\theta}(s)\approx Q^{\pi}(s, a)
\]
通过机器学习的方法我们一旦近似了价值函数或者是动作价值函数就可以通过一些策略进行控制，比如 \(\epsilon\)-greedy。

那么我们简单回顾下 RL 的学习目标：通过 agent 与环境进行交互，获取累计回报最大化。既然我们最终要学习如何与环境交互的策略，那么我们可以直接学习策略吗，而之前先近似价值函数，再通过贪婪策略控制的思路更像是"曲线救国"。
这就是本篇文章的内容，我们如何直接来学习策略，用数学的形式表达就是：
\[\pi_{\theta}(s, a) = P[a | s, \theta]\]

这就是被称为策略梯度（Policy Gradient，简称PG）算法。

当然，本篇内容同样的是针对 model-free 的强化学习。

Value-Based vs. Policy-Based RL

Value-Based：

• 学习价值函数
• Implicit policy，比如 \(\epsilon\)-greedy

Policy-Based：

• 没有价值函数
• 直接学习策略

Actor-Critic：

• 学习价值函数
• 学习策略

三者的关系可以形式化地表示如下：

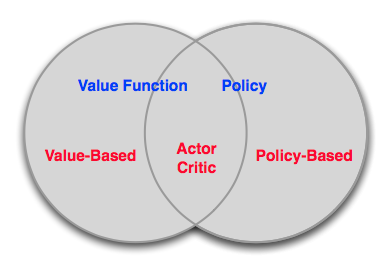
认识到 Value-Based 与 Policy-Based 区别后，我们再来讨论下 Policy-Based RL 的优缺点：

优点：

• 收敛性更好
• 对于具有高维或者连续动作空间的问题更加有效
• 可以学习随机策略

缺点：

• 绝大多数情况下收敛到局部最优点，而非全局最优
• 评估一个策略一般情况下低效且存在较高的方差

Policy Search

我们首先定义下目标函数。

Policy Objective Functions

目标：给定一个带有参数 \(\theta\) 的策略 \(\pi_{\theta}(s, a)\)，找到最优的参数 \(\theta\)。
但是我们如何评估不同参数下策略 \(\pi_{\theta}(s, a)\) 的优劣呢？

• 对于episode 任务来说，我们可以使用start value：
  \[J_1(\theta)=V^{\pi_{\theta}}(s_1)=E_{\pi_{\theta}}[v_1]\]
• 对于连续性任务来说，我们可以使用 average value：
  \[J_{avV}(\theta)=\sum_{s}d^{\pi_{\theta}}(s)V^{\pi_{\theta}}(s)\]
  或者每一步的平均回报：
  \[J_{avR}(\theta)=\sum_{s}d^{\pi_{\theta}}(s)\sum_{a}\pi_{\theta}(s, a)R_s^a\]
  其中 \(d^{\pi_{\theta}}(s)\) 是马尔卡夫链在 \(\pi_{\theta}\) 下的静态分布。

Policy Optimisation

在明确目标以后，我们再来看基于策略的 RL 为一个典型的优化问题：找出 \(\theta\) 最大化 \(J(\theta)\)。
最优化的方法有很多，比如不依赖梯度（gradient-free）的算法：

• 爬山算法
• 模拟退火
• 进化算法
• ...

但是一般来说，如果我们能在问题中获得梯度的话，基于梯度的最优化方法具有比较好的效果：

• 梯度下降
• 共轭梯度
• 拟牛顿法
• ...

我们本篇讨论梯度下降的方法。

策略梯度定理

假设策略 \(\pi_{\theta}\) 为零的时候可微，并且已知梯度 \(\triangledown_{\theta}\pi_{\theta}(s, a)\)，定义 \(\triangledown_{\theta}\log\pi_{\theta}(s, a)\) 为得分函数（score function）。二者关系如下：
\[\triangledown_{\theta}\pi_{\theta}(s, a) = \triangledown_{\theta}\pi_{\theta}(s, a) \frac{\triangledown_{\theta}\pi_{\theta}(s, a)}{\pi_{\theta}(s, a)}=\pi_{\theta}(s, a)\triangledown_{\theta}\log\pi_{\theta}(s, a)\]
接下来我们考虑一个只走一步的MDP，对它使用策略梯度下降。\(\pi_{\theta}(s, a)\) 表示关于参数 \(\theta\) 的函数，映射是 \(p(a|s,\theta)\)。它在状态 \(s\) 向前走一步，获得奖励\(r=R_{s, a}\)。那么选择行动 \(a\) 的奖励为 \(\pi_{\theta}(s, a)R_{s, a}\)，在状态 \(s\) 的加权奖励为 \(\sum_{a\in A}\pi_{\theta}(s, a)R_{s, a}\)，应用策略所能获得的奖励期望及梯度为：
\[
J(\theta)=E_{\pi_{\theta}}[r] = \sum_{s\in S}d(s)\sum_{a\in A}\pi_{\theta}(s, a)R_{s, a}\\
\triangledown_{\theta}J(\theta) = \color{Red}{\sum_{s\in S}d(s)\sum_{a\in A}\pi_{\theta}(s, a)}\triangledown_{\theta}\log\pi_{\theta}(s, a)R_{s, a}=E_{\pi_{\theta}}[\triangledown_{\theta}\log\pi_{\theta}(s, a)r]
\]

再考虑走了多步的MDP，使用 \(Q^{\pi_{\theta}}(s, a)\) 代替奖励值 \(r\)，对于任意可微的策略，策略梯度为：
\[\triangledown_{\theta}J(\theta) = E_{\pi_{\theta}}[\triangledown_{\theta}\log\pi_{\theta}(s, a)Q^{\pi_{\theta}}(s, a)]\]

策略梯度定理

对于任意可微策略 \(\pi_{\theta}(s, a)\)，任意策略目标方程 \(J = J_1, J_{avR}, ...\)，策略梯度：
\[\triangledown_{\theta}J(\theta) = E_{\pi_{\theta}}[\triangledown_{\theta}\log\pi_{\theta}(s, a)Q^{\pi_{\theta}}(s, a)]\]

蒙特卡洛策略梯度算法（REINFORCE）

Monte-Carlo策略梯度算法，即REINFORCE：

• 通过采样episode来更新参数：；
• 使用随机梯度上升法更新参数；
• 使用return \(v_t\) 作为 \(Q^{\pi_{\theta}}(s_t, a_t)\) 的无偏估计

则 \(\Delta\theta_t = \alpha \triangledown_{\theta}\log\pi_{\theta}(s_t, a_t)v_t\)，具体如下：

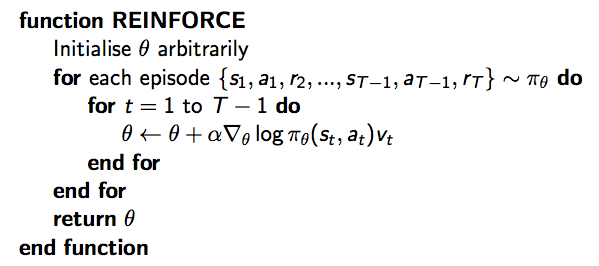
Actir-Critic 策略梯度算法

Monte-Carlo策略梯度的方差较高，因此放弃用return来估计行动-价值函数Q，而是使用 critic 来估计Q：
\[Q_w(s, a)\approx Q^{\pi_{\theta}}(s, a)\]
这就是大名鼎鼎的 Actor-Critic 算法，它有两套参数：

• Critic：更新动作价值函数参数 \(w\)
• Actor： 朝着 Critic 方向更新策略参数 \(\theta\)

Actor-Critic 算法是一个近似的策略梯度算法：
\[
\triangledown_\theta J(\theta)\approx E_{\pi_{\theta}}[\triangledown_{\theta}\log \pi_{\theta}(s, a)Q_w(s, a)]\\
\Delta\theta = \alpha\triangledown_\theta\log\pi_{\theta}(s,a)Q_w(s,a)
\]

Critic 本质就是在进行策略评估：How good is policy \(\pi_{\theta}\) for current parameters \(\theta\).
策略评估我们之前介绍过MC、TD、TD(\(\lambda\))，以及价值函数近似方法。如下所示，简单的 Actir-Critic 算法 Critic 为动作价值函数近似，使用最为简单的线性方程，即：\(Q_w(s, a) = \phi(s, a)^T w\)，具体的伪代码如下所示：

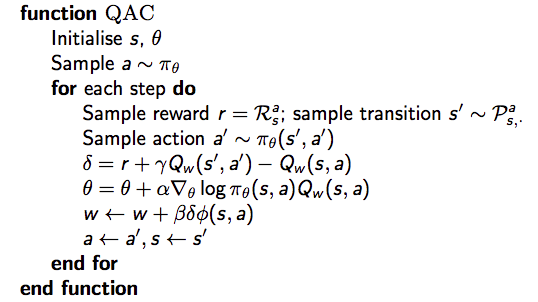
在 Actir-Critic 算法中，对策略进行了估计，这会产生误差（bias），但是当满足以下两个条件时，策略梯度是准确的：

• 价值函数的估计值没有和策略相违背，即：\(\triangledown_w Q_w(s,a) = \triangledown_\theta\log\pi_{\theta}(s,a)\)
• 价值函数的参数w能够最小化误差，即：\(\epsilon = E_{\pi_{\theta}}[(Q^{\pi_{\theta}}(s, a) - Q_w(s,a))^2]\)

优势函数

另外，我们可以通过将策略梯度减去一个基线函数（baseline funtion）B(s)，可以在不改变期望的情况下降低方差（variance）。证明不改变期望，就是证明相加和为0：
\[
\begin{align}
E_{\pi_{\theta}}[\triangledown_\theta\log\pi_{\theta}(s,a)B(s)]
&=\sum_{s\in S}d^{\pi_{\theta}}(s)\sum_a \triangledown_\theta\pi_{\theta}(s, a)B(s)\\
&=\sum_{s\in S}d^{\pi_{\theta}}(s)B(s)\triangledown_\theta\sum_{a\in A}\pi_{\theta}(s,a )\\
&= 0
\end{align}
\]

状态价值函数 \(V^{\pi_{\theta}}(s)\) 是一个好的基线。因此可以通过使用优势函数（Advantage function）\(A^{\pi_{\theta}}(s,a)\) 来重写价值梯度函数。
\[
A^{\pi_{\theta}}(s,a)=Q^{\pi_{\theta}}(s,a)-V^{\pi_{\theta}}(s)\\
\triangledown_\theta J(\theta)=E_{\pi_{\theta}}[\triangledown_\theta\log\pi_{\theta}(s,a)A^{\pi_{\theta}}(s,a)]
\]

设 \(V^{\pi_{\theta}}(s)\) 是真实的价值函数，TD算法利用bellman方程来逼近真实值，误差为 \(\delta^{\pi_{\theta}}=r+\gamma V^{\pi_{\theta}}(s') - V^{\pi_{\theta}}(s)\)。该误差是优势函数的无偏估计。因此我们可以使用该误差计算策略梯度：
\[\triangledown_\theta J(\theta)=E_{\pi_{\theta}}[\triangledown_\theta\log\pi_{\theta}(s,a)\delta^{\pi_{\theta}}]\]
该方法只需要critic，不需要actor。更多关于 Advantage Function 的可以看这里。

最后总结一下策略梯度算法：

Reference

[1] Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto, 2018
[2] David Silver's Homepage
[3] Advantage Learning