BUAA-OO-第一单元总结

BUAA-OO第一单元博客总结

---

第一次作业总结

（1）类关系图

　　　　　　

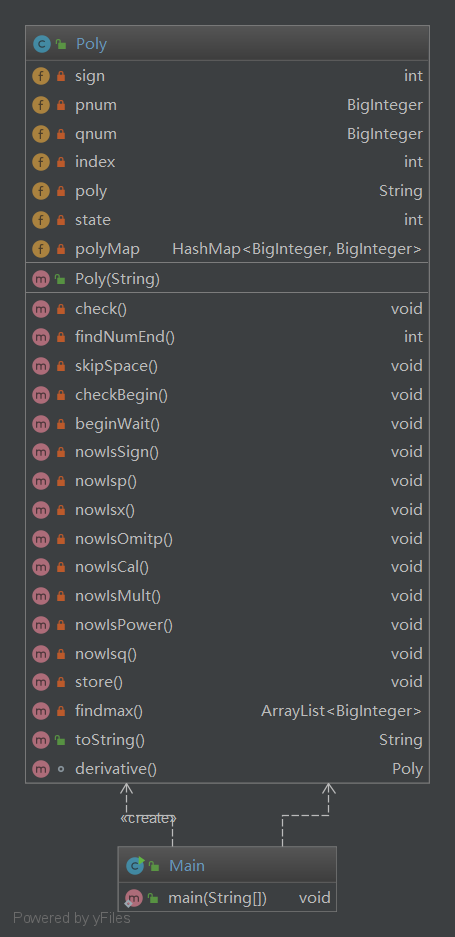
• 第一次作业类图关系简单，仅有一个Poly封装类以及一个Main主类调用Poly，Poly封装类内部完成了包括对象构造，求导，生成字符串的一系列函数。

（2）作业设计思路：

• 由于刚刚开始接触面向对象编程，对面向对象的概念仅简单的理解为对象封装，因此第一次作业构造的程序其实仅仅只是面向过程思想的一个变形。第一次作业由于不想写又大又长的正则表达式，同时也想使自己的程序便于后续的debug，因此构造了状态机的方式来进行字符串验证与处理。处理完后同步进行合并同类项等操作，并单独构造求导函数对处理后的表达式进行求导，同时重写toString函数进行输出。

（3）类与方法内部分析：

　　Poly类：

• 属性：

  • PolyMap为表达式存储的hashmap，以幂函数指数为index，所乘系数为value构成。其余属性均为构造函数过程中所使用的全局变量。pnum代表当前所分割项系数，sign代表当前分割项的符号，qnum代表当前分割项的指数，state为状态机的状态，poly为输入的字符串。

• 方法：

  • 从图中check方法一直到store方法均为状态机的内部方法，其中状态有十个，剩余为过程处理函数。findmax方法为toString方法调用时先调用的一个内部函数，目的是将表达式系数最大的元素放在头部，使得输出时可以省略一个‘+’号。toString方法将表达式翻译为字符串，derivative方法为求导方法，该方法返回一个新的Poly对象。由于状态机的缘故，大部分状态方法内部嵌套了多个if语句块，因此显得逻辑臃肿复杂，结构复杂度也大大增加。

• 由于第一次作业对面向对象编程思想了解的还不够深刻，因此所有属性设置均带有面向过程的色彩。其具体的方法复杂度数据如下图：　　　　　　　　　　

　　　　　　

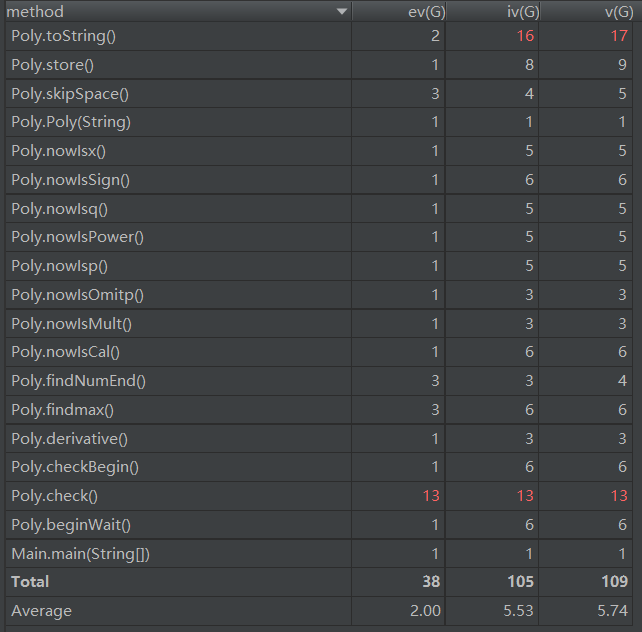
（4）优缺点分析：

• 优点：　

  • 通过状态机的方式检验表达式合法性，避免了长正则可能出现的爆栈，同时也能在测试过程清晰的知道自己在哪一个地方出现了bug便于修改

  • 状态机在分割各个因子和常数时很方便，能实时存入到hashmap中进行合并同类项。

  • 将求导方法和构造方法分割开，便于后续修改。

  • 表达式为不可变对象，避免了在后续操作过程操作不当出现bug

• 缺点：

  • 状态机状态冗多，且对题目要求依赖性很强，不便于后续题目的继承

  • 没有设置专门的因子类，仅仅单有一个表达式类可修改性非常弱，仅能支持本次作业，难以继承到下一次作业

  • 状态机逻辑表达式复杂，if语句嵌套层数多，容易致使程序结构复杂，不易维护。

---

第二次作业总结

（1）类关系图

　　　　　　

（2）作业设计思路

• 第二次作业设计与第一次相比较，多了一些子类，而不再是一个臃肿的Expression类。利用子类对数据进行分类包装，在通过Expression类将各个封装的子类关系相连接。第二次作业设计也舍去了第一次的状态机。由于状态机的设计不好对各个子对象进行区分，因此采用分割表达式的方法，将表达式分割成各个乘积项以构成乘积项对象，再构造新的指数类，将各个乘积项按照指数不同的方式区分开喂给Expression类，Expression类对象中的hashmap储存各个乘积项的集合以便进行合并同类项操作。Expression类同时完成求导工作，其求导即调用子对象Item的求导方法，将各个Item分别求导组成新的表达式。

• 第二次作业额外实现了ExpressionBetter类，将优化类单独分割开一方面增加了各个类的独立性以及能够减少Expression类的内部变量个数，不必因为要实现优化方法而增加一堆平时不需要使用的变量和属性，降低其复杂度。

　　分割表达式思路：

• 本次作业分割表达式的思路采取了状态机和正则表达式相互结合的方式，先在Expression类中构造方法实现将字符串分割的形式，利用加减号将表达式分割成各个独立的乘积项，将分割成的乘积项子项喂给Item构造函数，构造一个个乘积项对象，Item构造函数中利用split方法将乘积项分割成一个个独立的子函数，再解析子函数的指数和系数，最终组合成一个完整乘积项。Expression根据构造完成的乘积项构造其对应的Index对象，Index对象有三个分量，分别代表幂函数，sin和cos函数的指数，利用Index属性区分各个Item的不同。将一个个<Index,Item>对储存在hashmap中并方便合并同类项。

　　优化表达式思路：

• • 本次优化表达式采用了暴力的广度搜索方法，优化的方向有三个（只进行和化简，不进行拆化简），分别为：

1. 1. A*sin(x)^2+B*cos(x)^2 = (A-B)*sin(x)^2+B=(B-A)*cos(x)^2+A
   2. A-B*cos(x)^2 = A*sin(x)^2-(B-A)*cos(x)^2 = B*sin(x)^2+(A-B)
   3. A-B*sin(x)^2 = A*cos(x)^2-(B-A)*sin(x)^2 = B*cos(x)^2+(A-B)

• • 具体策略为：对Expression内的每个Item进行搜索，寻找是否有另一个与该Item满足化简要求的Item，若有，则对表达式进行变换，并入队记录长度。以此类推。当遍历完当前表达式的所有Item之后将队头的表达式出队，再次进行上述过程。整个bfs结束之后输出最短的表达式。

• 经过实践验证可得，该方法也许不能每次都将表达式化至最简，但大部分情况都能够化到最短，有少部分情况会出现TLE或者不能化至最简情况。

（3）类与方法分析

　　Expression类：

• 　属性：

  • 　items为一个存放Item的hashmap，描述了整个表达式的各个乘积项（合并同类项后的），lenth记录表达式的长度，用于后续化简工作描述表达式长度

• 　方法：　　

  • 　构造方法由两种形式，第一种是解析字符串构建新的表达式对象，另一种是复制已有的表达式对象，便于后续化简工作。

  • 　add方法有两种形式，一种是将Item加入到当前表达式中，用于构造表达式，另一种是将求得的Expression对象和当前Expression对象相加，用于求导组成新的表达式。

  • 　derivative方法返回一个新的表达式，为当前表达式求导后的表达式，通过调用每个Item的求导方法之后将每个Item求导结果add成一个新的表达式。

  • 　toString方法将表达式翻译成字符串形式用于输出。

  • 　其他方法用于化简。

　　Item类：

• 　属性：

  • 　pnum为乘积项的系数，qnum为乘积项的指数，为一个Index对象，是一个三维向量记录三种函数的指数。

• 　方法：

  • 构造方法有两种形式，一种是传递乘积项的系数和指数构造，另一种是解析字符串构建

  • 　add方法是将两个指数相同的Item系数相加，构成新的表达式。

  • 　derivative方法是将Item进行求导，返回一个新的Expression对象。

  • 　toString方法是将Item翻译成字符串。

  • 　其余方法为构造中或者化简中使用

　　Index类：

• 　属性：

  • 　有三个分量，分别记录sin函数，cos函数和幂函数的指数

• 　方法：

  • 　重写的hashcode方法用于区分不同Index，便于Expression中的hashmap检索。

  • 　重写的equals方法同上作用

  • 　Mult方法将两个不同的Index相加，用于乘积项相乘时改变Index。

  • 　三个get方法返回不同函数的指数。

　　ExpressionBetter类：

• 　属性：

  • 　min记录当前最短的表达式长度，result记录最终化简结果，剩余变量为bfs过程中的全局变量。

• 　方法：

  • 　feed方法将表达式喂进该类，进行bfs化简。

  • 　getResult方法用于返回上一次化简的结果。

  • 　targetcheck为private方法，用于检测当前可化简方向。

　　各个类与方法的复杂度量如下：

　　　　　　　　　　

　　　　　　　　

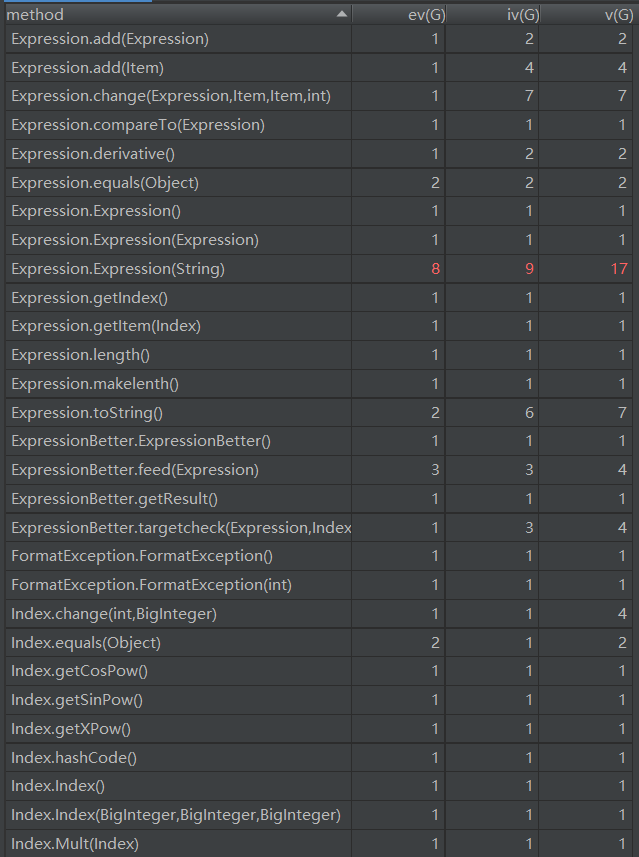
　　可以观察到各个类的构造方法复杂度都偏高，因为采用的是状态机和正则相结合的形式，if语句嵌套层数大，因此逻辑复杂度高。

（4）本次作业的bug

• 本次作业的bug主要有两个，第一个是split的用法失误导致表达式验证过程中出现bug，第二个是表达式化简优化过程中不考虑一定的终止条件导致TLE发生。

• 对于第一个bug，由于Item类中通过split过程中出现的bug，具体代码如下：

  private Index newx(int i, String ss) throws FormatException {
         String[] xs = ss.split("\\^",-1);
         String x1 = "[ \\t]*[-][ \\t]*x[ \\t]*";
         String x2 = "[ \\t]*[+][ \\t]*x[ \\t]*";
         String x = "[ \\t]*x[ \\t]*";
         if (xs.length > 2) {
             throw new FormatException();
         } else if (xs.length > 0)
         ......

• 在第二行的split语句中一开始没有加上-1参数，会导致split出的空字符被自动略去，因此只要出现类似‘x^’的非法数据，出现没有报WRONG FORMAT！的bug

• 对于第二个bug，在优化的bfs中一开始没有加入搜索层数的限制，会导致一些数据在优化过程陷入不收敛且无限的优化情况，因此为了避免出现TLE的情况，为bfs限制了最大500的搜索数并且采用优先队列的方式存储入队的表达式，以表达式长度最短的放在队头，以尽量保证用最少的优化次数优化出最好的效果。

（5）优缺点分析

• 　优点：　

  • 　本次作业舍弃了上一次作业臃肿的状态机的设计，将表达式分割为项的更小对象，实现了更好的封装，而不再是一整个Expression的臃肿大类，不便于实现具体功能。

  • 　实现多类后类与类之间关系也比较清晰，Item为各个乘积项，Expression为Item的集合，通过Index来索引

  • 　将优化类和表达式类分隔开，即能使其各自完成各自的任务，也能避免优化嵌套在表达式类中造成表达式类的臃肿。

• 　缺点：　

  • 　字符串解析没有单独写成一个类而仍是嵌套在各个类中，致使各个类即使分割开了仍无法被下一次任务继承，因为更换格式要求将导致解析功能作废，整个类无法继承。

  • 　没有将sin和cos和x分割成三个类，并不能很好的区分各个类。

---

第三次OO作业

（1）类关系图

　　　　　　

（2）作业设计思路

• • 本次作业设计之前首先明确了各个类的区分与关系。表达式中根据层次分为三大类：表达式类（Expression），乘积项类（Term），因子类（Factor），Expression有若干个Term组合，而Term也由若干个Factor相乘组合，而Factor又可再细分为sin，cos，power，digital和expression_Factor，因此Factor之中可以嵌套Expression（如sin，cos，expression_Factor），也可以不嵌套而形成单因子。

  • 因此，根据需求，首先构建了Factor抽象类，具有求导等抽象方法，而SinFactor，CosFactor，PowerFactor，ExpressionFactor，DigitalFactor均为该抽象类子类。其中SinFactor，CosFactor具有Factor分量，代表内嵌的Factor，ExpressionFactor中具有Expression分量，代表内嵌的表达式。至此，各个类基本构建完成。

  • 此外，此次作业为了完成前两次均不可继承的缺陷，在各个表达式类中不进行字符串解析，而将字符串解析交给单独的ExpressionBuilder类去完成，从而使类的功能单独开而不受题目条件限制。

  • 对于题目功能的实现，首先字符串解析采取了递归下降的方式完成，表达式的优化嵌套在字符串解析之中（只进行求导前拆括号的优化，不进行求导后提取公因式优化），对可拆括号进行拆除并且适当的合并同类项。

　　字符串解析：

• • 表达式的构建主要分为几个步骤：解析表达式，解析乘积项，解析项内因子，解析因子内因子或表达式，因此构建了构造表达式，构造项，构造因子的函数，构造表达式会调用构造项函数，将构造成的各个项组合成为表达式，构造项函数调用构造因子函数，将各个因子组合成一个项，而构造因子函数会识别因子类型，根据可嵌套的规则适当调用构造因子或者构造表达式函数，形成递归。

　　表达式优化：

• • 此次作业由于时间问题没有足够时间构造单独优化类对表达式进行优化，因此想在解析字符串过程去除多余括号对表达式进行优化，以便在构造过程中进行合并同类项等操作。因此此次优化重点我只放在拆括号。对于输入的表达式可拆括号的情况分为以下几种：

1. 1. A*(Expr) + Expr 第一个项为仅含有表达式因子和常数因子的项，因此将常数因子乘给表达式因子中表达式的各个项，将表达式因子括号拆去。

   2. sin((Factor)) / cos((Factor)) / ((Factor)) sin或者cos函数中的因子为表达式因子，而该表达式因子仅含有一个乘积项且该项仅含有一个因子，因此可以拆除多余括号，表达式因子同理。

   3. (Factor*Factor*Factor)*Term 该项中前半部分的表达式因子仅含有一个项，因此可以将其外围括号拆除合并成一个项。

• • 经过实践检验，该（假）优化方法和大多数同学的优化方法在一定程度上可以化简至相近的长度，且耗时并不长。

（3）类属性和方法分析

　　 Expression类：

• 　属性：

  • 　terms为存放该表达式各个项的ArrayList

• 　方法：

  • 　add方法有两种形式，一种是和表达式相加生成新的表达式，另一种是往表达式中加入新的Term

  • 　mult方法用于表达式化简，将系数乘入表达式各个项中以便拆括号

  • derivative方法为求导方法，将各个项求导后相加形成求导后的表达式。

  • 　equals方法用于合并同类项。

  • 　toString方法翻译成字符串。

　　Term类：

• 　属性：

  • 　pnum为该项的系数，即项内所有digital乘积，factors为该项中所有Factor的集合

• 　方法：

  • 　add为两个具有相同factors的Term系数相加，合并同类项。

  • 　mult有两种形式，一种是和Factor相乘，一种是和Term相乘，均是为该项增加factor

  • 　equals方法用于合并同类项。

  • 　toString翻译为字符串

  • 　其余方法用于化简表达式

　　Factor类：

• 　属性：

  • 　拥有子类SinFactor，CosFactor，PowerFactor，DigitalFactor，ExpressionFactor，分别代表四种不同的Factor。

• 　方法：

  •     derivative方法用于求导，符合链式求导法则

  • 　getIndex用于返回该Factor的系数

  • 　equals比较Factor是否相等，用于合并同类项。

  • 　toString方法翻译为字符串。

　　ExpressionBuilder类：

• 　属性：

  • 　result为构造的表达式

• 　方法：

  • 　makeExpression方法为构造表达式方法，返回一个表达式。

  • 　makeTerm方法为构造Term方法，返回一个Term

  • 　makeFactor方法为调度构造Factor的总方法

  • 　剩余方法为构造各个不同的Factor并进行拆括号。

　　各个类的复杂度度量如下：　　

　　　　　　

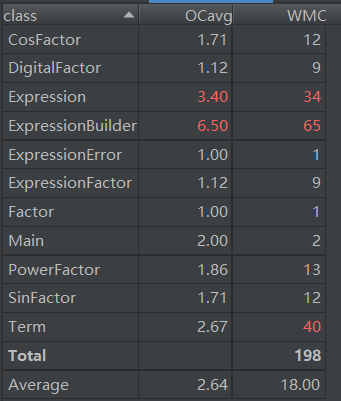
　　由于Builder方法中if语句嵌套多，因此复杂度高，而Expression和Term类为了使表达式化简更加方便增加了一些判定可否化简的方法，因此if语句也较多。

（4）优缺点分析

• 　优点：　

  • 　此次构建类将解析类和存储数据的子类分开，使得子类能够完成各自的非题目要求限制地工作，使得可继承可维护性增加。

  • 　构建Factor抽象类，使得在对不同因子操作时均可以向上转型为Factor类而使用其共性，简化了结构。

  • 　采用递归的方式构建表达式和求导。

• 　缺点：　

  • 　在字符串解析过程仍使用大量的if语句来判定表达式合法，使结构复杂。

  • 　优化方面存在缺陷，不能保证优化后长度是否变短。

  • 　表达式类中仍然为了可化简加入了一些化简的方法，使得类仍不够独立，仍依赖于题目要求。

---

互测过程找bug策略

　　第一单元互测阶段，我是采取构建自动化评测脚本和人工查bug相互进行的方式来找别人程序中的bug。

　　自动化脚本构建：

• 第一单元三次作业的互测采取的是对拍的方式来找别人的bug。自动对拍脚本构建需要三份代码支持：数据生成器、检查器、bash脚本。数据生成器利用当次作业的要求自动生成随机的测试数据，检查器使用python的sympy包，通过表达式相减是否为0来评判表达式是否相等，若不等则带入随机值进行计算是否相等。bash脚本则进行调度，将数据生成器生成的数据喂给java程序运行，记录结果，并将所有结果送入检查器检查。

• 第一次作业主要针对格式检查，以及对于长正则表达式是否会出现爆栈行为。

• 第二次作业更加针对于化简出错或者TLE或者求导出错检查，专门构造了可以生成可化简数据的数据生成器（根据自己的化简方式构建）进行对拍。

• 第三次作业主要针对于是否会在化简过程中出现WRONG FORMAT形式的输出，比如sin(2*x)

　　人工评测方式：

• 人工检查bug主要检查在输入层面上有没有对字符串进行正确的处理，以及构造一些比较特殊的自动化脚本不能生成的数据，比如多行输入以及长输入，检查程序是否忽略多行或者爆栈。

---

设计模式思考

• 对于前两次作业，本人对于面向对象构造思想仍停留在只要对对象进行很好的封装并且对具体功能进行独立化实现，而并没有考虑到多态以及继承的实现。因此结束了前两次作业之后，发现了严重的问题：

  • 在设计过程中经常需要对对象进行重构，而不能沿用上一作业相似的结构。

  • 第三次作业因子类型众多，若不采取一种统一的方式将他们联系起来将会导致存储结构非常臃肿复杂。

• 因此对于第三次作业，深刻的思考了前两次作业犯下的问题，得出一些结论：

  • 面向对象构造的意义在于既能独立的完成此次实验工作，又能沿用到之后相似的工作，因此需要尽可能地将当前实验特殊要求和对象的通性功能进行分割开，例如单独构建解析字符串类，而不要嵌套在各个子类之中，否则更换任务需求之后这些子类均不可用需要再次重构。

  • 引入了抽象类，将所有的不同的因子类都作为该类的子类，这样在存储过程中可以向上转型成统一类型，便于存储。

• 此外，对于可变与不可变对象的思考，在第三次试验中，本人将底层的因子全部设计为不可变对象，而顶层的表达式为可变对象，这样设计只是为了方便化简，因为若均为不可变对象将会导致在每一次化简过程中都需要重新clone一样的对象，这对于较长的表达式是需要一定时间的，而如果括号嵌套的多则更需要不断的调用化简函数，会导致程序运行效率降低。

---

总结

• 关于设计

  • 要区分好题目特殊要求和对象特殊功能，将对象特殊功能在对象中实现，而重新建立新的Builder类来实现题目的特殊需求。

  • 对不可变对象设计需要谨慎，对于大长数据结构若需要进行多次操作则尽可能设计为可变对象而减少clone使用。

  • 减少代码重复率，减少不必要工作。

  • 尽可能减少多if嵌套

• 关于优化　　
  • 对优化算法设计要考虑其时间复杂度，避免出现TLE情况。

  • 尽量将优化独立成一个类，也尽量不要在表达式类中为可优化增加特殊方法，增加表达式类的可继承性。

• 关于测试
  • 对拍器设计不仅要设计正确数据的验证，还要对进行WRONG数据的验证。

  • 仍需要手构一些对拍器不能实现的特殊数据，包括特殊字符等，完备验证程序正确性。