『字典树 trie』

<更新提示>

<第一次更新>

---

<正文>

字典树 (trie)

字典树，又名\(trie\)树，是一种用于实现字符串快速检索的树形数据结构。核心思想为利用若干字符串的公共前缀来节约储存空间以及实现快速检索。

\(trie\)树可以在\(O((n+m)*len)\)解决形如这样的字符串检索问题:

给定\(n\)个字符串，再给定\(m\)个询问，每次询问某个字符串在这\(n\)个字符串中出现了多少次

特点

\(trie\)树最显著的特点是，当它存储的若干个字符串有公共前缀时，它将不会重复存储。

与其他树形数据结构不同的是，\(trie\)树的大部分信息都储存在边的指针上，节点只按照题意储存若干特殊信息，如该位置是否作为一个单词的结尾等。以储存英文单词的\(26\)叉\(trie\)树为例，我们可以用如下方式储存。

\(Code:\)

const int SIZE=2e6+20;//代表字符集的大小
int trie[SIZE][26],t=1;//trie[i][j]代表trie树中节点i的第j个字符指针，若该指针不存在，则指向0，t代表trie树中当前最后一个节点的编号

如图，这是一棵\(trie\)树。

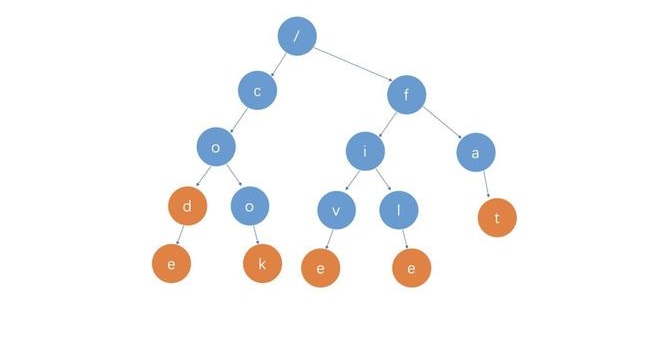
\(trie\)树没有什么很重要的性质，所以我们直接探讨如何实现\(trie\)树。

插入 (insert)

\(trie\)树要能够实现插入一个新的字符串\(S\)，这是最基础的操作。

首先，我们设置一个当前位置的指针\(p\)，令\(p=1\)，即指向根节点，然后依次扫描\(S\)当中的每一个字符\(c\):

• 1.若节点\(p\)的字符指针\(c\)指向一个存在的节点\(q\)，那么就说明当前这个字符串和以前的某个字符串是有公共前缀的，直接令\(p=q\)即可。
• 2.若节点\(p\)的字符指针\(c\)指向空，则说明当前这个字符串和以前的任何字符串都没有了公共前缀，我们需要新增一个节点\(q\)，令\(c\)指向\(q\)，再令\(p=q\)。

当\(S\)完成插入时，在末尾位置\(p\)标注:节点\(p\)是一个结束位置的节点。

\(Code:\)

inline void insert(char k[])//插入字符串k
{
	int p=1,len=strlen(k);
	for(int i=0;i<len;i++)
	{
		if(!trie[p][k[i]-'a'])//指针不存在
			trie[p][k[i]-'a']=++t;
		p=trie[p][k[i]-'a'];
	}
	end[p]=true;
}

检索 (retrieval)

trie当然还要实现检索操作啦。其实，插入查找和检索操作几乎是相同的，对于检索串\(S\)，设置一个当前位置的指针\(p\)，令\(p=1\)，然后依次扫描\(S\)当中的每一个字符\(c\):

• 1.若节点\(p\)的字符指针\(c\)指向一个存在的节点\(q\)，令\(p=q\)，继续检索。
• 2.若节点\(p\)的字符指针\(c\)指向空，则说明\(S\)没有被插入过trie树，结束检索。
• 3.直到字符串\(S\)被检索完毕，返回\(end[p]\)。

为什么要返回\(end[p]\)呢？还有一种情况是检索的字符串是某个已有字符串的前缀，所以检索是不会以为字符指针指向空而退出，所以我们还要判断:最后的位置是否作为字符串的结尾。

\(Code:\)

inline bool retrieval(char str[])
{
	int len=strlen(str),p=1;
	for(int i=0;i<len;i++)
	{
		p=trie[p][str[i]-'a'];
		if(!p)return false;
	}
	return end[p];
}

总结

再回看之前的图片，我们可以彻底明白了\(trie\)树原理。

这棵\(trie\)树其实储存了\(cod\)，\(code\)，\(cook\)，\(five\)，\(file\)，\(fat\)，这六个字符串，而对于公共的前缀，\(trie\)只储存了一次，这就是\(trie\)树的核心所在。

对于一个字符串的结尾，图中也使用了黄色节点标注。

重要的一点是，\(trie\)的空间复杂度一般比较难以计算，准确的来说，空间复杂度为\(O(nc)\)，\(n\)为插入的字符串个数，\(c\)为字符集的大小，也就是所以字符串的并，可以认为$$c=\bigcup^{n}_{i=1}S_i$$

通常来说，记得开大一点就好了嘛。

前缀统计

Description

给定N个字符串S1,S2...SN，接下来进行M次询问，每次询问给定一个字符串T，求S1～SN中有多少个字符串是T的前缀。输入字符串的总长度不超过10^6，仅包含小写字母。

Input Format

第一行两个整数N，M。接下来N行每行一个字符串Si。接下来M行每行一个字符串表示询问。

Output Format

对于每个询问，输出一个整数表示答案

Sample Input

3 2
ab
bc
abc
abc
efg

Sample Output

2
0

解析

这也算是一道比较模板的\(trie\)树了吧。先插入每一个字符串，然后只要将每一个节点额为地记录一个\(cnt\)值，代表到该节点结束的字符串数量，再在检索的时候累加沿路所有\(cnt\)值即可。

\(Code:\)

#include<bits/stdc++.h>
using namespace std;
#define mset(name,val) memset(name,val,sizeof name)
#define filein(str) freopen(str".in","r",stdin)
#define fileout(str) freopen(str".out","w",stdout)
const int SIZE=1e6+20;
int trie[SIZE][26],cnt[SIZE],t=1;
int n,m;char s[SIZE];
inline void insert(char str[])
{
	int len=strlen(str),p=1;
	for(int i=0;i<len;i++)
	{
		if(!trie[p][str[i]-'a'])
			trie[p][str[i]-'a']=++t;
		p=trie[p][str[i]-'a'];
	}
	cnt[p]++;
}
inline int retrieval(char str[])
{
	int len=strlen(str),p=1,res=0;
	for(int i=0;i<len;i++)
	{
		p=trie[p][str[i]-'a'];
		if(!p)return res;
		res+=cnt[p];
	}
	return res;
}
inline void input(void)
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%s",s);
		insert(s);
	}
	for(int i=1;i<=m;i++)
	{
		scanf("%s",s);
		printf("%d\n",retrieval(s));
	}
}
int main(void)
{
	input();
	return 0;
}

The XOR Largest Pair

Description

在给定的N个整数A1，A2……AN中选出两个进行xor运算，得到的结果最大是多少？

Input Format

第一行一个整数N，第二行N个整数A1～AN。

Output Format

一个整数表示答案。

Sample Input

3
1 2 3

Sample Output

3

解析

这就算是一道\(trie\)树的运用了吧。我们把每一个数字看为一个\(32\)的的二进制字符串，对于每一个输入\(a\)，将其二进制串插入\(trie\)树中，并检索\(a\)的二进制串，由于异或运算不同得\(1\)，相同得\(0\)，所以每一次往与当前位不同的指针尝试访问，如果不行，再访问与当前位相同的指针。

这样，就能够在\(trie\)树中检索到与\(a\)异或值最大的数，取出后模拟进行异或运算，更新答案即可。

关于\(32\)位二进制数，可以用\(STL\ bitset\)，会方便许多。

\(Code:\)

#include<iostream>
#include<cstdio>
#include<vector>
#include<bitset>
#include<cstring>
using namespace std;
#define filein(str) freopen(str".in","r",stdin)
#define fileout(str) freopen(str".out","w",stdout)
const int N=1e5+20,SIZE=1e5*32+20;
int n,trie[SIZE][2],d[N],t=1,ans=0;
struct LINK{int val,ver;};
vector < LINK > e[N];
inline void input(void)
{
	for(int i=1;i<n;i++)
	{
		int x,y,v;
		scanf("%d%d%d",&x,&y,&v);
		x++,y++;
		e[x].push_back((LINK){v,y});
		e[y].push_back((LINK){v,x});
	}
}
inline void dfs(int x,int fa)
{
	for(int i=0;i<e[x].size();i++)
	{
		int y=e[x][i].ver;
		if(fa==y)continue;
		if(x!=1)d[y]=d[x]^e[x][i].val;
		else d[y]=e[x][i].val;
		dfs(y,x);
	}
}
inline bitset<32> calc(int x)
{
	bitset<32> res;
	int temp[40],cnt=32;
	while(x)
	{
		if(1&x)temp[--cnt]=1;
		else temp[--cnt]=0;
		x>>=1;
	}
	while(cnt-1)temp[--cnt]=0;
	for(int i=0;i<32;i++)
		res[i]=temp[i];
	return res;
}
inline void insert(bitset<32> k)
{
	int p=1;
	for(int i=0;i<32;i++)
	{
		if(!trie[p][k[i]])
			trie[p][k[i]]=++t;
		p=trie[p][k[i]];
	}
}
inline int retrieval(bitset<32> k)
{
	int p=1;bitset<32> best;
	for(int i=0;i<32;i++)
	{
		if(trie[p][k[i]^1])
		{
			best[i]=k[i]^1;
			p=trie[p][k[i]^1];
		}
		else if(trie[p][k[i]])
		{
			best[i]=k[i];
			p=trie[p][k[i]];
		}
		else break;
	}
	best=best^k;
	int res=0;
	for(int i=0;i<32;i++)
		res+=(best[i]<<(32-i-1));
	return res;
}
inline void solve(void)
{
	bitset<32> p;
	for(int i=1;i<=n;i++)
	{
		p=calc(d[i]);
		insert(p);
		ans=max(ans,retrieval(p));
	}
}
inline void reset(void)
{
	memset(trie,0,sizeof trie);
	memset(d,0,sizeof d);
	ans=0;t=1;
	for(int i=1;i<=n;i++)
		e[i].clear();
}
int main(void)
{
	while(~scanf("%d",&n))
	{
		input();
		dfs(1,0);
		solve();
		printf("%d\n",ans);
		reset();
	}
	return 0;
}

---

<后记>