Python四步实现决策树ID3算法，参考机器学习实战

一、编写计算历史数据的经验熵函数

from math import log
def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for elem in dataSet: #遍历数据集中每条样本的类别标签，统计每类标签的数量
        currentLabel = elem[-1]
        if currentLabel not in labelCounts.keys(): #如果当前标签不在字典的key值中，则初始化该标签对应的值为0
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1             #计数+1
    shannonEnt = 0.0
    for key in labelCounts:#开始计算历史数据的经验熵
        prob = float(labelCounts[key])/numEntries#每类标签在全部历史数据中所占概率
        shannonEnt -= prob * log(prob,2) #log base 2
    return shannonEnt

二、按照指定特征和其特征值来划分数据集

参数axis指定是第几个特征，value是该特征什么值，这个函数会在第三步的函数和第四步里被调用，主要作用在相应步结束后介绍

def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for elem in dataSet:
        if elem[axis] == value:
            reducedFeatElem=elem[:axis]
            reducedFeatElem.extend(elem[axis+1:])
            retDataSet.append(reducedFeatElem)
    return retDataSet

三、计算每个特征的熵，求得信息增益，返回使得信息增益最大的特征

比较难理解的就是第二个for迭代中的内容，会在这个函数编写结束后解释，其他的解释就直接注释在代码中了

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1      #统计特征数目
    baseEntropy = calcShannonEnt(dataSet)  #计算历史数据的经验熵
    bestInfoGain = 0.0; bestFeature = -1
    for i in range(numFeatures):        #迭代所有特征
        featList = [sample[i] for sample in dataSet]#创建所有样本中每一个样本的这个特征的取值
        uniqueVals = set(featList)       #获得该特征的取值集合，即剔除重复的特征取值
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)#按照条件经验熵熵的公式计算i列特征取值为value的条件下的条件经验熵
        infoGain = baseEntropy - newEntropy     #计算信息增益
        if (infoGain > bestInfoGain):       #与目前最大的信息增益比较
            bestInfoGain = infoGain         #更新最大信息增益
            bestFeature = i                 #更新使得信息增益最大的特征列i
    return bestFeature                      #returns an integer

chooseBestFeatureToSplit函数调用splitDataSet的作用就是获得axis列特征的取值为value的样本，splitDataSet函数返回值长度用于计算axis列特征取值为value时的样本占全部样本数量的概率，返回值作为参数传递给calcShannonEnt函数可以计算axis列特征取值为value时的经验熵

四、递归构建决策树

递归结束的条件是：程序已经遍历完样本数据的全部特征列或者所有实例样本属于同一类（即标签类别相同）

另外，如果所有实例样本标签类别相同则得到一个叶子节点

（一）定义叶子节点中的实例类别

主要是当划分数据集的全部属性已经处理完，该叶子节点中的实例样本的类别标签不是唯一的，如何定义该叶子节点的最终类别，此时采用多数表决的方法决定

import operator
def majorityCnt(classList):
    classCount={}
    for classlabel in classList:
        if classlabel not in classCount.keys():
            classCount[classlabel] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

(二）、构造决策树

参数dataSet为传入的数据集，labels为特征名

def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]#获取传入数据集的类别标签列表
    if classList.count(classList[0]) == len(classList): #当传入数据集的类且标签全部相同时停止递归
        return classList[0]
    if len(dataSet[0]) == 1: #当传入的数据集只剩一个标签列时（每次调用划分数据集函数splitDataSet时都会删除一个特征列）停止递归
        return majorityCnt(classList) #返回标签列表中类别数量最多的类别
    bestFeat = chooseBestFeatureToSplit(dataSet) #调用chooseBestFeatureToSplit选择最优特征
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}} #使用字典存储每次迭代中的最优特征
    del(labels[bestFeat])
    featValues = [sample[bestFeat] for sample in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]       #copy all of labels, so trees don't mess up existing labels
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
    return myTree 

createTree函数难理解的部分在for迭代里，作用就是对于当前最优特征的不同取值构建分支，每一个特征取值可以构建出一个分支，具体是利用for循环对于当前最优特征的每个取值value下，递归调用createTree函数，参数为调用splitDataSet函数（以当前最优特征列，以及最优特征取值作为参数）返回dataSet中满足最优特征对应的列取值为value剔除了该最优特征列的样本数据集

 以上四大步骤就实现了基本的ID3算法，下面编写一个创建数据集的函数（背后的意义是：判断是否为鱼类假设由两个特征就可以判断，分别是“不浮出水面是否可以生存”，“是否脚蹼”）来测试算法

def createDataSet():
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    labels = ['no surfacing','flippers']
    #change to discrete values
    return dataSet, labels

测试：

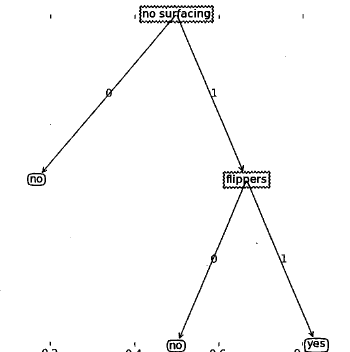
mytree字典的含义如图：

五、利用以上实现的算法实现决策树分类，需要递归遍历整棵决策树

def classify(inputTree,featLabels,testVec):
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)#为了确定某个特征在数据集的位置
    key = testVec[featIndex]
    valueOfFeat = secondDict[key]
    if isinstance(valueOfFeat, dict):
        classLabel = classify(valueOfFeat, featLabels, testVec)
    else: classLabel = valueOfFeat
    return classLabel

测试：

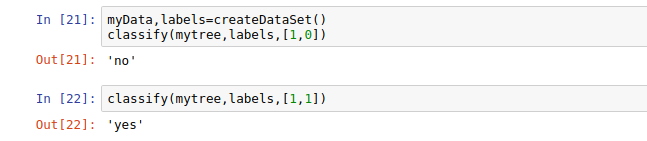
对应数据集标签可以看到分类正确，结束啦^.^