bfs与dfs基础

bfs像二叉树的层序遍历

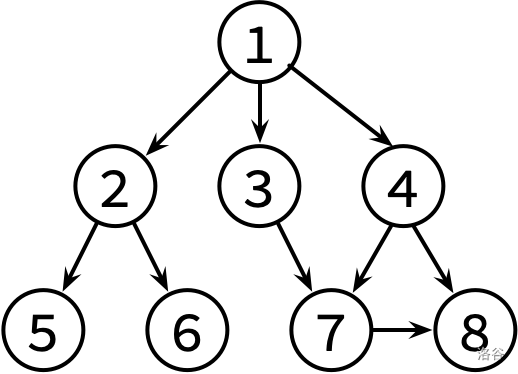
像这个图走bfs就{1， 2， 3， 4， 5， 6， 7， 8}这样走；

dfs就{1， 2， 5， 6， 3， 7， 8， 4}。

bfs与queue相结合，走到哪就把哪加进queue，出时把最先进的那个点弹出，同时把弹出这个点有关连的点加入queue。

例：LuoguP5318 dfs与bfs运用

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
ll n, m, k, q, p;
string s, r;
vector<int>a[maxn];//存该点可以走向哪些点，vector第二维可以一直存点
int b[maxn];//用来判断该点有木有经过

void dfs(int x){
    if(x >= 1 && x <= n){//经过就输出和标记
        b[x] = 1;
        cout<<x<<' ';
    }
    for(int i = 0; i < a[x].size(); i++){
        if(!b[a[x][i]])//把没经过的点dfs遍历一遍
            dfs(a[x][i]);
    }
    return;
}

void bfs(){
    queue<int>q;//队列存点
    q.push(1);//点1先进
    while(!q.empty()){//判断空否
        int p = q.front();
        if(b[p] == 0){//队首未经历就输出
            b[p] = 1;//标记
            cout<<p<<' ';
        }
        else{//经历过直接弹出到下一次循环
            q.pop();
            continue;
        }
        for(int i = 0; i < a[p].size(); i++){
            if(!b[a[p][i]])//把点p可以走向的点加入queue
                q.push(a[p][i]);
        }
        q.pop();//不要了弹出
    }
}

int main(){
    //ios_base::sync_with_stdio(0);
    //cin.tie(); cout.tie();
    cin>>n>>m;
    for(int i = 1; i <= m; i++){
        cin>>p>>q;
        a[p].push_back(q);//点p可以走向q
    }
    for(int i = 1; i <= n; i++){
        sort(a[i].begin(), a[i].end());//依题意从小到大排序，如果大到小自己写个cmp函数
    }
    dfs(1);//从1开始
    memset(b, 0, sizeof(b));//b数组归零用于bfs
    cout<<endl;
    bfs();
    return 0;
}

例：LuoguP3916 反向建边的dfs

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
ll n, m, k, q, p;
string s, r;
vector<int>a[maxn];
int b[maxn], c[maxn];//b标记，c存到达最大值

void dfs(int x){
    for(int i = 0; i < a[x].size(); i++){//a[x].size()是可以到x点的数
        if(b[a[x][i]] == 0){//看看是否标记
            b[a[x][i]] = 1;//现在经历了要标记
            c[a[x][i]] = c[x];//c[x]是x能到达的最大值，而a[x][i]能到x，所以它到最大值也是x能到最大值
            dfs(a[x][i]);//继续深搜可以到a[x][i]的点
        }
    }
}

int main(){
    //ios_base::sync_with_stdio(0);
    //cin.tie(); cout.tie();
    cin>>n>>m;
    for(int i = 1; i <= m; i++){
        cin>>p>>q;
        a[q].push_back(p);//反向建边，a[q]里为能到达q的点
    }
    for(int i = n; i >= 1; i--){//因为求到达最大，从n倒着循环就行
        if(b[i] == 0){//看看是否经历
            b[i] = 1;//现在要经历了标记
            c[i] = i;//自己到自己最大
            dfs(i);//深度搜能到i点的点把他们可以到达最大值设为i
        }
    }
    for(int i = 1; i <= n; i++)
        cout<<c[i]<<' ';//输出1到n能到的最大点
    return 0;
}

待续…