论文解读（PPNP）《Predict then Propagate: Graph Neural Networks meet Personalized PageRank》

论文信息

论文标题：Predict then Propagate: Graph Neural Networks meet Personalized PageRank
论文作者：Johannes Gasteiger, Aleksandar Bojchevski, Stephan Günnemann
论文来源：2019,ICLR
论文地址：download
论文代码：download

1-Abstract

　　本文主要将 PageRank 算法引入到 GNNs ，提出了  PPNP 模型 和APPNP 模型。

2-Introduction

　　问题：

• • 增大邻域范围，充分利用领域信息；【传播多层——消息传递机制的本质，也可以看做随机游走】
  • 解决过平滑问题（一般均为传播多层造成的过平滑）；

　　受 带重启随机游走（random walk）的影响，本文利用 personalized PageRank 代替随机游走 ，来增加传送到根节点的机会，以避免过平滑现象（主要是更多的考虑根节点的邻域），此外该模型允许使用更多的传播层数。【通过 $\text{Eq.4}$ 便于理解】

3 Graph convolutional networks and their limited range

　　半监督节点分类 GCN：

　　　　$\boldsymbol{Z}_{\mathrm{GCN}}=\operatorname{softmax}\left(\hat{\tilde{\tilde{A}}} \operatorname{ReLU}\left(\hat{\tilde{\tilde{A}}} \boldsymbol{X} \boldsymbol{W}_{0}\right) \boldsymbol{W}_{1}\right)  \quad\quad\quad(1)$

　　其中，$\hat{\tilde{\boldsymbol{A}}}=\tilde{\boldsymbol{D}}^{-1 / 2} \tilde{\boldsymbol{A}} \tilde{\boldsymbol{D}}^{-1 / 2}$。

　　存在的问题：【APPNP 所解决的问题 】

• • 不能使用更多的传播层，因为会造成过平滑；
  • 层数增加，参数量增加；

4 Personalized propagation of neural predictions

From message passing to personalized PageRank

　　早起版本 PageRank：

　　　　$\pi_{\mathrm{pr}}=A_{\mathrm{rw}} \pi_{\mathrm{pr}}, \quad\quad\text { with }\quad\quad A_{\mathrm{rw}}=A D^{-1}$

　　以及考虑根节点信息，提出 personalized PageRank 算法：【类似带重启的随机游走，缓解过平滑】

　　　　$\boldsymbol{\pi}_{\mathrm{ppr}}\left(\boldsymbol{i}_{x}\right)=(1-\alpha) \hat{\tilde{A}} \boldsymbol{\pi}_{\mathrm{ppr}}\left(\boldsymbol{i}_{x}\right)+\alpha \boldsymbol{i}_{x}$

　　其中：

• • $\hat{\tilde{A}}=\tilde{\boldsymbol{D}}^{-1 / 2} \tilde{\boldsymbol{A}} \tilde{\boldsymbol{D}}^{-1 / 2}$；
  • $i_x$ 表示初始根节点的特征；

　　计算得到平稳状态后的分布：

　　　　$\pi_{\mathrm{ppr}}\left(\boldsymbol{i}_{x}\right)=\alpha\left(\boldsymbol{I}_{n}-(1-\alpha) \hat{\tilde{ A}}\right)^{-1} \boldsymbol{i}_{x}$

　　用单位矩阵代替指标向量 $i_x$ 得  personalized PageRank matrix：

　　　　$\mathbf{\Pi}_{\mathrm{ppr}}=\alpha\left(\boldsymbol{I}_{n}-(1-\alpha) \hat{\tilde{ A }}\right)^{-1}$

　　$\mathbf{\Pi}_{\mathrm{ppr}}$ 中的元素 $yx$ 可以理解为 节点 $x$ 对节点 $y$ 的影响分数 $I(x, y) \propto \Pi_{\mathrm{ppr}}^{(y x)}$。【其实就是 节点 $x$ 转移到节点 $y$ 的概率值】

　　Note：上述式子可逆的时候需要满足  $\frac{1}{1-\alpha}>1$ 且不能为 $\hat{\tilde{A}}$ 的特征值。

　　借由上述阐述，得到 PPNP 模型：

　　　　$\boldsymbol{Z}_{\mathrm{PPNP}}=\operatorname{softmax}\left(\alpha\left(\boldsymbol{I}_{n}-(1-\alpha) \hat{\tilde{ A }}\right)^{-1} \boldsymbol{H}\right), \quad \boldsymbol{H}_{i,:}=f_{\theta}\left(\boldsymbol{X}_{i,:}\right)\quad\quad\quad(3)$

　　Note：直接计算  $\Pi_{\mathrm{ppr}}$ ，具有高计算复杂度且需要 $\mathcal{O}\left(n^{2}\right)$ 的内存空间。【APPNP 改进的地方】

Approximate personalized propagation of neural predictions (APPNP)

　　APPNP 通过幂次迭代逼近 topic-sensitive PageRank 来实现线性计算复杂度。传播过程为：

　　　　$\begin{array}{l}\boldsymbol{Z}^{(0)} &=&\boldsymbol{H}=f_{\theta}(\boldsymbol{X}) \\\boldsymbol{Z}^{(k+1)} &=&(1-\alpha) \hat{\tilde{A}} \boldsymbol{Z}^{(k)}+\alpha \boldsymbol{H} \\\boldsymbol{Z}^{(K)} &=&\operatorname{softmax}\left((1-\alpha) \hat{\tilde{\boldsymbol{A}}} \boldsymbol{Z}^{(K-1)}+\alpha \boldsymbol{H}\right)\end{array}\quad\quad\quad(4)$

　　这个迭代方案的收敛性证明如下：

　　

　　在 PPNP 和 APPNP 中，影响每个节点的邻域的大小都可以通过传送概率 $\alpha $ 进行调整。

附：图扩散

　　$\mathcal{T}_{\mathbf{A}}(\mathbf{A})=\sum_{k=0}^{\infty} \Theta_{k} \mathbf{S}^{k}$

其中：

• $\mathbf{S} \in \mathbb{R}^{N \times N}$  是广泛的转移矩阵
• $\Theta$  是加权系数，且  $\sum_{k=0}^{\infty} \Theta_{k}=1 ， \Theta_{k} \in[0,1]$

Personalized PageRank (PPR) kernal

　　其中：

• • $\mathbf{S}=\mathbf{D}^{-1 / 2} \mathbf{A D}^{-1 / 2}$
  • $\Theta_{k}=\alpha(1-\alpha)^{k}$

　　得：

• • $\mathcal{T}_{\mathbf{A}}^{P P R}(\mathbf{A})=\alpha\left(\mathbf{I}_{n}-(1-\alpha) \mathbf{D}^{-1 / 2} \mathbf{A} \mathbf{D}^{-1 / 2}\right)^{-1}$　　

5 Experimental setup

　　消息传递算法对 数据划分 和 权重初始化 都非常敏感。

Overall accuracy

　　

不同模型在随机数据划分 和 随机权重初始化的标准差

　　

Training time per epoch

　　

Training set size

　　

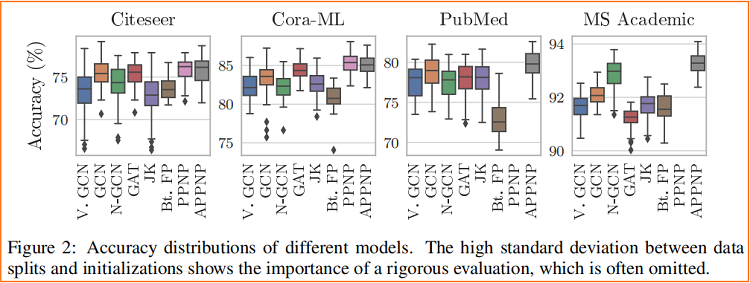
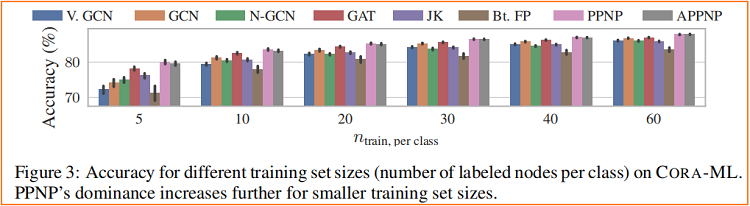
6 Conclusion

　　在本文中，我们介绍了神经预测(PPNP)及其快速近似APPNP。我们通过考虑GCN和PageRank之间的关系并将其扩展到个性化PageRank来导这个模型。这个简单的模型解耦了预测和传播，并解决了许多消息传递模型中固有的有限范围的问题，而没有引入任何额外的参数。它使用来自一个大的、可调节的（通过传送概率 $\alpha$）邻域的信息来对每个节点进行分类。该模型在计算上高效，优于目前最先进的研究，在多个图上的半监督分类方法。