CF1442D Sum （动态规划，线段树分治）

（

宋

体

字

看

起

来

真

舒

服

）

_{_{（宋体字看起来真舒服）}}

（宋体字看起来真舒服）​​

题

面

(

洛

谷

翻

译

)

题面_{_{(洛谷翻译)}}

题面(洛谷翻译)​​

给定

n

n

n个不降的数组。
有一个值

a

n

s

ans

ans，初始为

0

0

0
你需要进行如下操作

k

k

k次：

1.选择一个数组
2.把

a

n

s

ans

ans加上数组的第一个元素。
3.把数组的第一个元素删除。

请求出

a

n

s

ans

ans最大是多少。

所有数组的元素总个数

≤

1

0

6

,

n

,

k

≤

3000

\leq 10^6,n,k\leq 3000

≤106,n,k≤3000

输

入

(

笔

者

亲

自

翻

译

)

输入_{_{(笔者亲自翻译)}}

输入(笔者亲自翻译)​​

第一行包含两个整数

n

n

n and

k

k

k (

1

≤

n

,

k

≤

3
 

000

1 \le n, k \le 3\,000

1≤n,k≤3000 ): 分别是数组和操作的数量。

接下来的

n

n

n 行每一行包含一个数组。 每一行的第一个整数是

t

i

t_i

ti​ (

1

≤

t

i

≤

1

0

6

1 \le t_i \le 10^6

1≤ti​≤106 ): 第

i

i

i 个数组的大小。 后面

t

i

t_i

ti​ 个整数

a

i

,

j

a_{i, j}

ai,j​ (

0

≤

a

i

,

1

≤

…

≤

a

i

,

t

i

≤

1

0

8

0 \le a_{i, 1} \le \ldots \le a_{i, t_i} \le 10^8

0≤ai,1​≤…≤ai,ti​​≤108 ) 给出了第

i

i

i 个数组。

保证

k

≤

∑

i

=

1

n

t

i

≤

1

0

6

k \le \sum\limits_{i=1}^n t_i \le 10^6

k≤i=1∑n​ti​≤106。

样

例

样例

样例

i

n

p

u

t

input

input

3 3
2 5 10
3 1 2 3
2 1 20

o

u

t

p

u

t

output

output

26

题

解

题解

题解

转换一下模型，相当于一个背包问题，这个不用我多说了吧。

我们会发现一个结论：最后的最优操作一定是把一些数组全选完，最多一个数组只选部分。

S

t

e

p
  

1
  

证

明

结

论

Step\;1\;证明结论

Step1证明结论

我们要证这个结论，实际上要证最优操作不存在两个只选了部分的数组：

为了方便证明，我们定义两个数组总和相等的时候，两数组选的数量相差更大的更优

其实很简单，如果存在这么两个数组选了部分：

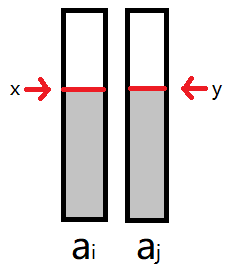
那么以下两种情况肯定更优：

1. a

   i

   ,

   x

   ≥

   a

   j

   ,

   y

   ⇒

   a

   i

   ,

   x

   +

   1

   ≥

   a

   j

   ,

   y

   :

   a_{i,x} ≥ a_{j,y} \Rightarrow a_{i,x+1} ≥ a_{j,y}:

   ai,x​≥aj,y​⇒ai,x+1​≥aj,y​:
   

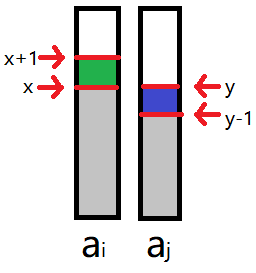
2. a

   i

   ,

   x

   ≤

   a

   j

   ,

   y

   ⇒

   a

   j

   ,

   y

   +

   1

   ≥

   a

   i

   ,

   x

   :

   a_{i,x} ≤ a_{j,y} \Rightarrow a_{j,y+1} ≥ a_{i,x}:

   ai,x​≤aj,y​⇒aj,y+1​≥ai,x​:
   

而这两种情况已经包含全集了（

a

i

,

x

≥

a

j

,

y

a_{i,x} ≥ a_{j,y}

ai,x​≥aj,y​ 和

a

i

,

x

≤

a

j

,

y

a_{i,x} ≤ a_{j,y}

ai,x​≤aj,y​），所以充分证明了 两个数组都没选完，在中间稳定 的情况是不存在的，因此最多就只有其中一个选完了，另一个没选完的情况。

S

t

e

p
  

2
  

利

用

结

论

Step\;2\;利用结论

Step2利用结论

这个结论怎么利用呢？

相当于我们如果确定某一个数组是只选部分的那一个，那么其他的数组就降维了、变成一个数了、一个物品了！

于是我们可以先把其他数组假设成只有一个数，然后把背包跑出来，最后暴力枚举只选部分的那个数组具体选几个。

那么，每一个数组一开始都有一个空的背包dp数组，表示该数组只选部分的情况下其他数组放进来处理的背包。但是这样还是

O

(

n

2

k

)

O(n^2k)

O(n2k) 的过不了。

我们可以想想怎么优化。我们发现每个数组

i

i

i 整个考虑会对

[

1

,

i

−

1

]

∪

[

i

+

1

,

n

]

[1,i-1]∪[i+1,n]

[1,i−1]∪[i+1,n] 内的其他数组的背包有贡献，这是两个区间，因此我们可以用线段树分治优化它，

这样一来每个数组就要对

l

o

g

n

logn

logn 个区间有贡献，而每次贡献是一次

O

(

m

)

O(m)

O(m) 的背包更新，时间复杂度

O

(

n

m

l

o

g

n

)

O(nmlogn)

O(nmlogn)。

最后，由于每个数组挂的区间有特殊性，可以不用真的建一棵线段树，直接判断挂在当前区间的数组有哪些就行了。

C

O

D

E

CODE

CODE

#include<queue>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 3005
#define LL long long
#define DB double
#define ENDL putchar('\n')//#define lowbit(x) ((-x)&(x))
LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s=='-')f = -f;s = getchar();}
	while(s >= '0' && s <= '9') {x=x*10+(s-'0');s = getchar();}
	return f * x;
}
const int MOD = 998244353;
int n,m,i,j,s,o,k,sq;
LL dp[100][MAXN];
bool f[100][MAXN];
vector<LL> a[MAXN];
int b[MAXN];
LL ans = 0;
void solve(int l,int r,int de) {
	memcpy(dp[de],dp[de-1],sizeof(dp[de]));
	memcpy(f[de],f[de-1],sizeof(f[de]));
	for(int i = 1;i <= n;i ++) {
		if(i == l) {
			i = r;continue;
		}
		if(!f[de][i]) {
			f[de][i] = 1;
			int tp = a[i][0];
			for(int j = m;j >= tp;j --) {
				dp[de][j] = max(dp[de][j],dp[de][j-tp] + a[i][tp]);
			}
		}
	}
	if(l < r) {
		int mid = (l + r) >> 1;
		solve(l,mid,de+1);solve(mid+1,r,de+1);
		return ;
	}
	else {
		int tp = a[l][0];
		ans = max(ans,dp[de][m]);
		for(int i = 1;i <= tp && i <= m;i ++) {
			ans = max(ans,dp[de][m-i] + a[l][i]);
		}
	}
	return ;
}
int main() {
	n = read();m = read();
	for(int i = 1;i <= n;i ++) {
		s = read();
		LL sm = 0;
		a[i].push_back(s);
		while(s --) {
			sm += read();
			a[i].push_back(sm);
		}
	}
	solve(1,n,1);
	printf("%lld\n",ans);
	return 0;
}