排序算法整理C++（初赛）

排序算法整理

常见考点

1. 将一个乱掉的字符串排回有序（以交换为基本操作）的最少操作，就是冒泡排序。
2. 排序算法的稳定性
3. 排序算法的时间复杂度

排序算法的稳定性

稳定性是指排序前两个元素a1 = a2，a1在前。排序过后，倘若a1始终在前，则算法是稳定的，否则是不稳定的。

稳定的

冒泡排序、插入排序、归并排序、基数排序

不稳定的

堆排序、快速排序、希尔排序、选择排序

各个算法细锁

冒泡排序

基本思路：双重循环遍历数组，交换两个相邻的逆序的数字。时间复杂度一般 - \(O(n^2)\)，最坏 - \(O(n^2)\)，最好\(O(n)\)。

代码

for(int i = 1; i <= n; i ++)
{
	for(int j = 1; j <= n - i; j ++)
    {
		if(a[j] > a[j + 1])
            swap(a[j], a[j + 1]);
    }
}

都说最优复杂度是O(N)，但显然这个程序怎么看都是\(O(n^2)\)，实际上\(O(n)\)是优化过的。考试的时候记住就行。

选择排序

基本思路：遍历一遍数组 i in (1, n + 1)，从 i 数开始遍历到后面，寻找最小的比它小的数，与它交换。

无论如何都是\(O(n^2)\)。

代码

for(int i = 1; i < n; i ++)
{
	int min = i;
    for(j = i + 1; j <= n; j ++)
    {
        if(a[min] > a[j])
            min = j;
        swap(a[i], a[min]);
    }
}

归并排序

分治思想，将数组中所有的数递归分为两个一组

网上讲的挺好的归并排序MergeSort（通俗易懂_kevinmeanscool的博客-CSDN

这个算法还能用来求逆序对，所以在复赛中也挺重要 虽然现在一般复赛不会考，只要在else后面（代码）加一句ans += mid - i +1，但我不知道原理。

代码

void merge_sort(int a[], int l, int r){
    if(l >= r)
        return;
    int mid = l + r >> 1;
    merge_sort(a, l, mid);
    merge_sort(a, mid + 1, r);
    int k = 0;
    int i = l;
    int j = mid + 1;
    while(i <= mid && j <= r){
        if(a[i] <= a[j])
            f[k ++] = a[i ++];
        else
            f[k ++] = a[j ++];
    }
    while(i <= mid) f[k ++] = a[i ++];
    while(j <= r) f[k ++] = a[j ++];
    for(i = l, j = 0; i <= r; i ++, j ++){
        a[i] = f[j];
    }
}

快速排序

基本思路：找一个基准数，先由i从左边出发，找到一个小于，j再从右边出发，找一个小于基准数的数。分开区间，重复此操作。时间复杂度平均\(O(nlon_n)\)，最优也是\(O(nlon_n)\)，最差\(O(n^2)\)。

代码

void qsort(int l, int r)
{
    int mid = a[l + r >> 1];
    int i = l, j = r;
    do{
        while(a[i] < mid) i ++;
        while(a[j] > mid) j --;
        if(i <= j)
        {
            swap(a[i], a[j]);
            i ++;
            j --;
        }
    }while(i <= j);
    if(l < j) qsort(l, j);
    if(i < r) qsort(i, r);
}
int main()
{
	qsort(1, n);
}

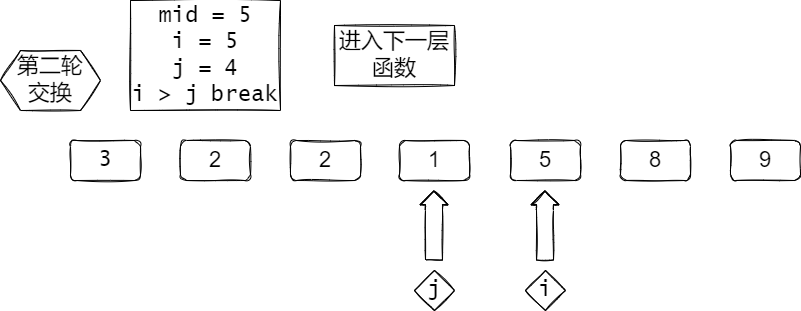
根据代码图解

（如果加载不出来请刷新，因为图放在Github）：

数组：[3, 2, 9, 5, 1, 8, 2]

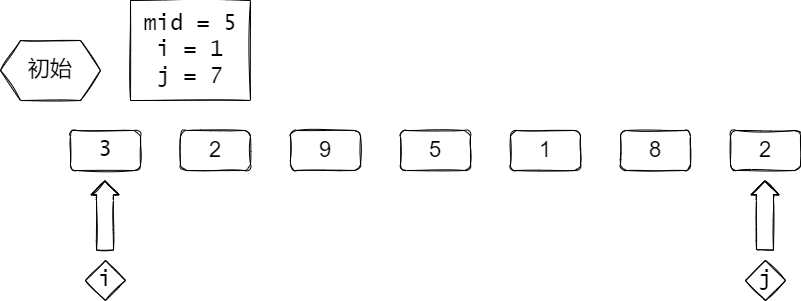
找到了

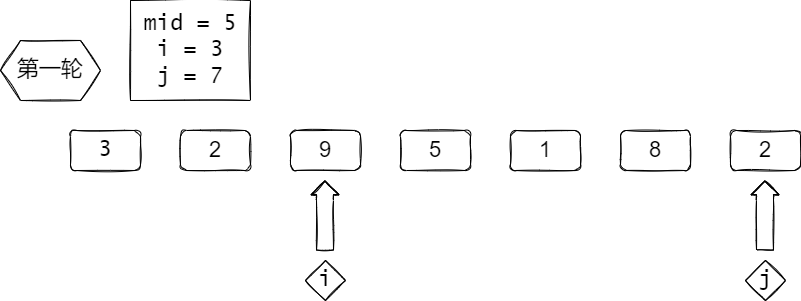
交换，注意i ++, j -- 不然会死循环

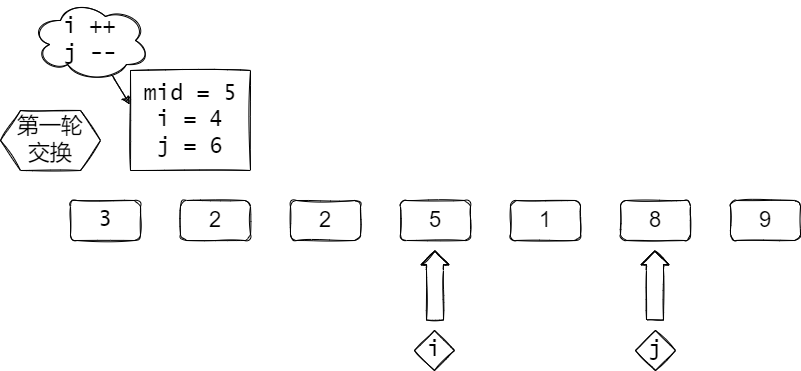
i 不再动了，因为a[i] = mid

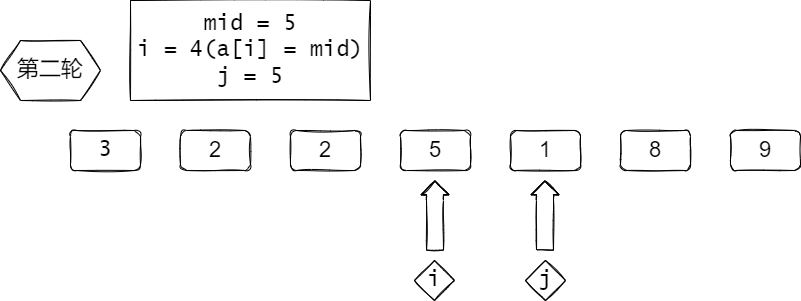
这里没写 i ++, j --