【公式详解】【优秀论文解读】EDPLVO: Efficient Direct Point-Line Visual Odometry

前言

多的不说哈 2022最佳优秀论文 来自美团无人机团队

作者提出了一种使用点和线的高效的直接视觉里程计（visual odometry，VO）算法—— EDPLVO 。他们证明了，2D 线上的 3D 像素点由 2D 线端点的逆深度决定，这使得将光度误差扩展到线变得可行。

直接进入正题

公式推导

首先直接看总误差



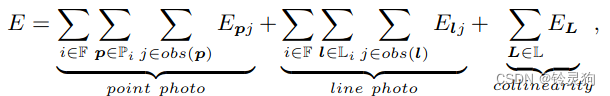
误差分为三部分：

\(E_{pj}\)误差为光度误差 这个被作者一笔带过了

\(E_{lj}\)误差为本文的重点 会重点讲解

\(E_{L}\)误差为线性约束 这个作者用了小篇幅来讲解

首先扔出光度误差公式：



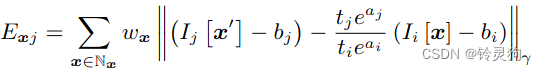
\(i\)和\(j\)对应两个相机视角 \(x\)就是两个视角看到的点

\(t\)为曝光时间 剩下的贴出来了 大家自行研读吧 或者查一查资料 这里其他的我不太能多解释了

核心误差构建

首先简单说一下普吕克坐标系 是将空间中的一个3D直线用两个在该直线上的3D点进行了表示



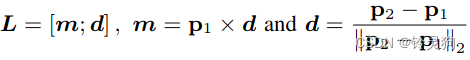
\(P_1\)和\(P_2\)就是线上的两个3D点

原理可以自行查阅一下 但是这个结论很清晰明了 不用做太多解释

下面来看 在普吕克坐标系表示下 点到该直线的距离为：



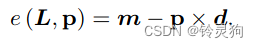
注意 这里用e进行表示了

接下来表示两个空间点：



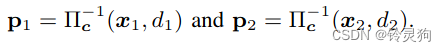
\(x_1\)和\(x_2\)为2d线的两个端点 \(d_1\)和\(d_2\)分别为这两个三维点的逆深度 那个像π似的是反投影矩阵 得到了这条线上的两个三维点坐标

然后结合上面的普吕克坐标表示的直线 就可以用上面两个三维点来表示直线了



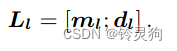
此时又来了一个不同于上面两个三维点的点 这个点依然在3D线上 这个点的光线的方向可以表示为：

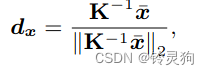
这里的 x 是图像坐标 且脑袋上带个横杠表示齐次坐标哈

然后就是很省略的一步 但是依然清晰明了：

我们需要求出上一个公式的 x 的三维坐标点：

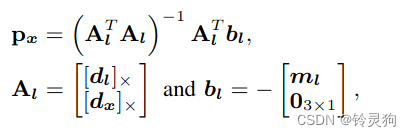
不好推但是公式很明白 这里的参数都在上面说过

\([]_x\)表示反对称矩阵哈

然后我们又将上式的这个三维点投影到另一个相机视角中：

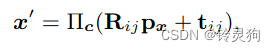
就得到了这个东西

这个东西带回到最上面的没太多解释的那个光度误差里 就得到了我们总公式的第二项的一部分

总公式的第二项详细的情况是：

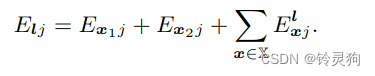
这里的前两项确实仍然是光度误差 第三项为我们刚才三维点投影到相机视角中再带入到光度误差的结果哈

从上面的推导结果可知 第三项只依赖于\(x_1\)和\(x_2\)的逆深度

第三种误差

接下来看第三种误差



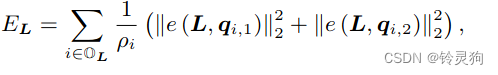
\(q\)是两个3D点 也是L的3D端点 \(e\)为定义的点到线的距离

然后还有前面那个东西的倒数 这个东西表示一个3D的L在相机视角下的一个投影2D线的长度 这个影响了\(q\)是否是端点的不确定度

然后这三种误差其实就这样建立起来了

H矩阵对比

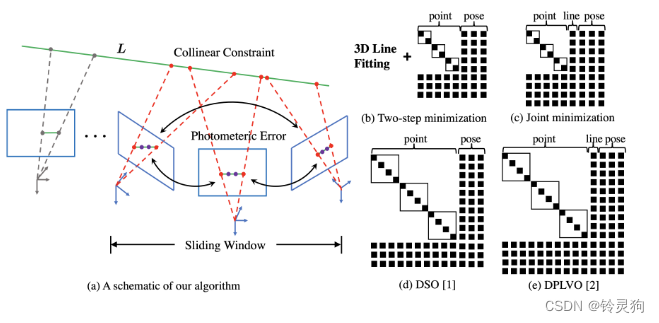
图b就是这个算法所得到的H矩阵 可以看出这个H矩阵相对于其他的H矩阵是最小的

原图片的描述贴上：



从这里也可以看到这个论文的优点。

主要贡献

在不增加变量数量和优化难度的情况下将线特征加入到了约束中，在不增加运算量的情况下提高了准确率。