遗传算法 Genetic Algorithms

遗传算法 Genetic Algorithms

遗传算法是一种“adaptive heuristic search algorithm”（自适应启发式搜索算法），虽不明、但觉厉。其实遗传算法的思路很朴素，实现起来也并不复杂（用到一点点生物学科普级别的知识，学科交叉还挺有趣的）。

遗传算法模拟的是自然界中，一个种群内生物基因的传递模式。可以预料到在大自然“优胜劣汰”的筛选机制下，那些能适应环境的强者往往更容易与配偶结合将自己的基因保留到下一代；而体弱多病的弱者会面临死亡，基因无法保存的下场。对于一个种群而言，这种淘汰机制可以让更多的优质基因得以留存，有利于种群的延续。

思路

现在我们假设：

• 问题的一个解，对应于一个“个体”（这是一种只有一个染色体的简单物种）
• 一个解应该由一个字符串来表示，其中一个字符对应于“基因”
• 存在一个判断机制来充当“优胜劣汰”机制，帮助我们判断哪些解更有价值
• 并让这些解“交配”，期望在下一代解中优质解变得更多

上图中有大、中、小三个红框：最小的代表一个解是由一个字符串，或者数字字符排列组合而成的；中间的指一个完整的解；而最大的红框则是指全体解集合（这里有优质解也有劣质解，需要我们甄别）

适应度函数

每一个解都有有一个，用来定量判断这个基因“竞争能力”的值，适应度函数。“竞争能力”更强的个体有更高的概率活到下一代，或者与配偶繁衍子代；但是由于种群内个体的数量是固定的，那些“竞争能力”弱的个体会死掉，被其它“竞争能力”更强的个体取代。

这样、下一代群体中个体的适应度函数的平均值会高于上一代（也就是这些解是问题更佳的解）。当父代与子代群体中的个体之间没有明显差异了，代表进化收敛了，这个算法也就找到了最优质的解。

变异

自然界中，决定后代基因的不仅仅是爹娘双方染色体的融合，还包括变异。引入变异可以提高种群个体的多样性，有利于提高种群的平均适应度函数，进而找到最优解。

算法流程

在原始种群被生成后（通常是随机出来的），遗传算法会采取以下措施来产生下一代：

1. 选择环节

对于适应度函数高的个体，给予更大的优先级来让它们保存与繁衍

1. 交配环节

对于从“选择环节”中调出的两个个体，让它们随机地结合，产生后代（就像两个染色体整合形成新的染色休那样！）。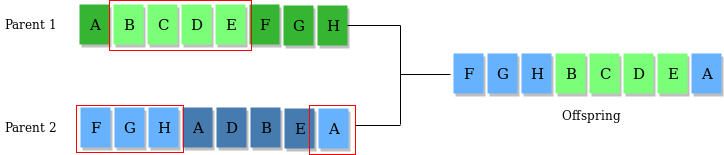

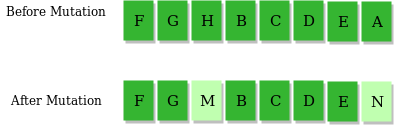
1. 变异环节

以相对较小的概率任意改变子代的若干基因，提高种群差异性，防止种群进化的进程过早地收敛。

用遗传算法完成一次光荣的进化！

用遗传算法打印，“welcome to ticmis's blog”

C++

// C++ program to create target string, starting from
// random string using Genetic Algorithm

#include <bits/stdc++.h>
using namespace std;

// Number of individuals in each generation
#define POPULATION_SIZE 100

// Valid Genes
const string GENES = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOP"\
"QRSTUVWXYZ 1234567890,'.-;:_!\"#%&/()=?@${[]}";

// Target string to be generated
const string TARGET = "Welcome to ticmis's blog";

// Function to generate random numbers in given range
int random_num(int start, int end)
{
    int range = (end-start)+1;
    int random_int = start+(rand()%range);
    return random_int;
}

// Create random genes for mutation
char mutated_genes()
{
    int len = GENES.size();
    int r = random_num(0, len-1);
    return GENES[r];
}

// create chromosome or string of genes
string create_gnome()
{
    int len = TARGET.size();
    string gnome = "";
    for(int i = 0;i<len;i++)
        gnome += mutated_genes();
    return gnome;
}

// Class representing individual in population
class Individual
{
public:
    string chromosome;
    int fitness;
    Individual(string chromosome);
    Individual mate(Individual parent2);
    int cal_fitness();
};

Individual::Individual(string chromosome)
{
    this->chromosome = chromosome;
    fitness = cal_fitness();
};

// Perform mating and produce new offspring
Individual Individual::mate(Individual par2)
{
    // chromosome for offspring
    string child_chromosome = "";

    int len = chromosome.size();
    for(int i = 0;i<len;i++)
    {
        // random probability
        float p = random_num(0, 100)/100;

        // if prob is less than 0.45, insert gene
        // from parent 1
        if(p < 0.45)
            child_chromosome += chromosome[i];

        // if prob is between 0.45 and 0.90, insert
        // gene from parent 2
        else if(p < 0.90)
            child_chromosome += par2.chromosome[i];

        // otherwise insert random gene(mutate),
        // for maintaining diversity
        else
            child_chromosome += mutated_genes();
    }

    // create new Individual(offspring) using
    // generated chromosome for offspring
    return Individual(child_chromosome);
};

// Calculate fitness score, it is the number of
// characters in string which differ from target
// string.
int Individual::cal_fitness()
{
    int len = TARGET.size();
    int fitness = 0;
    for(int i = 0;i<len;i++)
    {
        if(chromosome[i] != TARGET[i])
            fitness++;
    }
    return fitness;
};

// Overloading < operator
bool operator<(const Individual &ind1, const Individual &ind2)
{
    return ind1.fitness < ind2.fitness;
}

// Driver code
int main()
{
    srand((unsigned)(time(0)));

    // current generation
    int generation = 0;

    vector<Individual> population;
    bool found = false;

    // create initial population
    for(int i = 0;i<POPULATION_SIZE;i++)
    {
        string gnome = create_gnome();
        population.push_back(Individual(gnome));
    }

    while(! found)
    {
        // sort the population in increasing order of fitness score
        sort(population.begin(), population.end());

        // if the individual having lowest fitness score ie.
        // 0 then we know that we have reached to the target
        // and break the loop
        if(population[0].fitness <= 0)
        {
            found = true;
            break;
        }

        // Otherwise generate new offsprings for new generation
        vector<Individual> new_generation;

        // Perform Elitism, that mean 10% of fittest population
        // goes to the next generation
        int s = (10*POPULATION_SIZE)/100;
        for(int i = 0;i<s;i++)
            new_generation.push_back(population[i]);

        // From 50% of fittest population, Individuals
        // will mate to produce offspring
        s = (90*POPULATION_SIZE)/100;
        for(int i = 0;i<s;i++)
        {
            int len = population.size();
            int r = random_num(0, 50);
            Individual parent1 = population[r];
            r = random_num(0, 50);
            Individual parent2 = population[r];
            Individual offspring = parent1.mate(parent2);
            new_generation.push_back(offspring);
        }
        population = new_generation;
        cout<< "Generation: " << generation << "\t";
        cout<< "String: "<< population[0].chromosome <<"\t";
        cout<< "Fitness: "<< population[0].fitness << "\n";

        generation++;
     }
     cout<< "Generation: " << generation << "\t";
    cout<< "String: "<< population[0].chromosome <<"\t";
    cout<< "Fitness: "<< population[0].fitness << "\n";
}

Python3

# Python3 program to create target string, starting from
# random string using Genetic Algorithm

import random

# Number of individuals in each generation
POPULATION_SIZE = 100

# Valid genes
GENES = '''abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOP
QRSTUVWXYZ 1234567890,'.-;:_!"#%&/()=?@${[]}'''

# Target string to be generated
TARGET = "Welcome to ticmis's blog"

class Individual(object):
    '''
    Class representing individual in population
    '''
    def __init__(self, chromosome):
        self.chromosome = chromosome
        self.fitness = self.cal_fitness()

    @classmethod
    def mutated_genes(self):
        '''
        create random genes for mutation
        '''
        global GENES
        gene = random.choice(GENES)
        return gene

    @classmethod
    def create_gnome(self):
        '''
        create chromosome or string of genes
        '''
        global TARGET
        gnome_len = len(TARGET)
        return [self.mutated_genes() for _ in range(gnome_len)]

    def mate(self, par2):
        '''
        Perform mating and produce new offspring
        '''

        # chromosome for offspring
        child_chromosome = []
        for gp1, gp2 in zip(self.chromosome, par2.chromosome):    

            # random probability
            prob = random.random()

            # if prob is less than 0.45, insert gene
            # from parent 1
            if prob < 0.45:
                child_chromosome.append(gp1)

            # if prob is between 0.45 and 0.90, insert
            # gene from parent 2
            elif prob < 0.90:
                child_chromosome.append(gp2)

            # otherwise insert random gene(mutate),
            # for maintaining diversity
            else:
                child_chromosome.append(self.mutated_genes())

        # create new Individual(offspring) using
        # generated chromosome for offspring
        return Individual(child_chromosome)

    def cal_fitness(self):
        '''
        Calculate fitness score, it is the number of
        characters in string which differ from target
        string.
        '''
        global TARGET
        fitness = 0
        for gs, gt in zip(self.chromosome, TARGET):
            if gs != gt: fitness+= 1
        return fitness

# Driver code
def main():
    global POPULATION_SIZE

    #current generation
    generation = 1

    found = False
    population = []

    # create initial population
    for _ in range(POPULATION_SIZE):
                gnome = Individual.create_gnome()
                population.append(Individual(gnome))

    while not found:

        # sort the population in increasing order of fitness score
        population = sorted(population, key = lambda x:x.fitness)

        # if the individual having lowest fitness score ie.
        # 0 then we know that we have reached to the target
        # and break the loop
        if population[0].fitness <= 0:
            found = True
            break

        # Otherwise generate new offsprings for new generation
        new_generation = []

        # Perform Elitism, that mean 10% of fittest population
        # goes to the next generation
        s = int((10*POPULATION_SIZE)/100)
        new_generation.extend(population[:s])

        # From 50% of fittest population, Individuals
        # will mate to produce offspring
        s = int((90*POPULATION_SIZE)/100)
        for _ in range(s):
            parent1 = random.choice(population[:50])
            parent2 = random.choice(population[:50])
            child = parent1.mate(parent2)
            new_generation.append(child)

        population = new_generation

        print("Generation: {}\tString: {}\tFitness: {}".\
              format(generation,
              "".join(population[0].chromosome),
              population[0].fitness))

        generation += 1

    print("Generation: {}\tString: {}\tFitness: {}".\
          format(generation,
          "".join(population[0].chromosome),
          population[0].fitness))

if __name__ == '__main__':
    main()

Output:

Generation: 0 String: BLQx{m?"d}#tz#zXQ"#xw1Pv Fitness: 22

Generation: 1 String: WokJyv' a.oH{4Ch6u.EyK$_ Fitness: 22

Generation: 2 String: r&s4Sd7f![MAm?_R9#5 f3wg Fitness: 22

Generation: 3 String: r&s4Sd7f![MAm?_R9#5 f3wg Fitness: 22

Generation: 4 String: r&s4Sd7f![MAm?_R9#5 f3Zg Fitness: 22

Generation: 5 String: BLQx{m?"d}#tz#zXQ"#xw1Pv Fitness: 22

Generation: 6 String: r&s4Sd7f![MAm?_R9#5 f3wg Fitness: 22

Generation: 7 String: [&s4Sd7f![MAm?_R9#5 f3Zg Fitness: 22

.

.

.

Generation: 858 String: Welcome to t'cmis's blog Fitness: 1

Generation: 859 String: Welcome to tTcmis's blog Fitness: 1

Generation: 860 String: Welcome to tCcmis's blog Fitness: 1

Generation: 861 String: Welcome to tCcmis's blog Fitness: 1

Generation: 862 String: Welcome to ticmis's blog Fitness: 0