Learning with Mini-Batch

在机器学习中，学习的目标是选择期望风险\(R_{exp}\)(expected loss)最小的模型，但在实际情况下，我们不知道数据的真实分布（包含已知样本和训练样本），仅知道训练集上的数据分布。因此，我们的目标转化为最小化训练集上的平均损失，这也被称为经验风险\(R_{emp}\)(empirical loss)。

严格地说，我们应该计算所有训练数据的损失函数的总和，以此来更新模型参数(Batch Gradient Descent)。但随着数据集的不断增大，以ImagNet数据集为例，该数据集的数据量有百万之多，计算所有数据的损失函数之和显然是不现实的。若采用计算单个样本的损失函数更新参数的方法(Stochastic Gradient Descent)，会导致\(R_{emp}\)难以达到最小值，而且在数值处理上不能使用向量化的方法提高运算速度。

于是，我们采取一种折衷的想法，即取一部分数据，作为全部数据的代表，让神经网络从这每一批数据中学习，这里的“一部分数据”称为mini-batch，这种方法称为mini-batch学习。

以下图为例，蓝色的线表示Batch Gradient Descent，紫色的线表示Stochastic Gradient Descent，绿色的线表示Mini-Batch Gradient Descent。

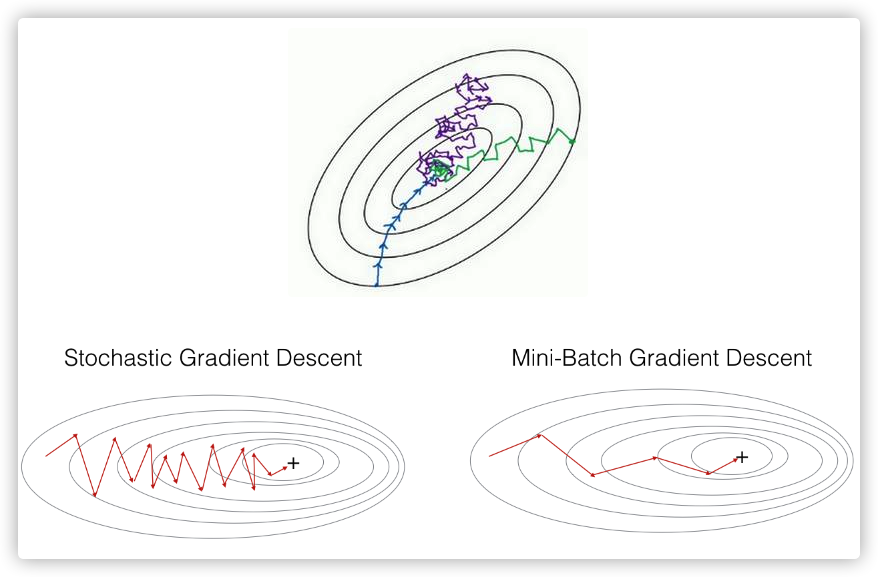
从上图可以看出，Mini-Batch相当于结合了Batch Gradient Descent和Stochastic Gradient Descent各自的优点，既能利用向量化方法提高运算速度，又能基本接近全局最小值。

对于mini-batch学习的介绍到此为止。下面我们将MINIST数据集上的分类问题作为背景，以交叉熵cross-entropy损失函数为例，来实现一下mini-bacth版的cross-entropy error。

给出cross-entropy error的定义如下:

\[E = - \sum_{k}t_k \log(y_k)\tag{1}
\]

其中\(y_k\)表示神经网络输出，\(t_k\)表示正确解标签。

等式1表示的是针对单个数据的损失函数，现在我们给出在mini-batch下的损失函数，如下

\[E = -\frac{1}{N}\sum_{n}\sum_{k}t_{nk}\log(y_{nk})\tag{2}
\]

其中N表示这一部分数据的数量，\(t_{nk}\)表示第n个数据在第k个元素的值（\(y_{nk}\)表示神经网络输出，\(t_{nk}\)表示监督数据）

我们来看一下用Python如何实现mini-batch版的cross-entropy error。针对监督数据\(t_{nk}\)的标签形式是否为one-hot，我们分类讨论处理。

此外，需要明确的一点是，对于一个分类神经网络，最后一层经过softmax函数处理后，输出\(y_{nk}\)是一个\(n\)x\(k\)的矩阵，\(y_{ij}\)表示第i个数据被预测为\(j(0 \leq j\leq10)\)的概率，特别地，当\(N=1\)时，\(y\)是一个包含10个元素的向量，类似于[0.1,0.2...0.3]，其中0.1表示输入数据预测为0的概率为0.1，0.2表示将输入数据预测为1的概率为0.2，其他情况以此类推。

首先，对于\(t_{nk}\)为one-hot表示的情况，代码块1如下

def cross_entropy_error(y,t):
    batch_size = y.shape[0]
    return -np.sum(t * np.log(y + 1e-7)) / batch_size

在上面的代码中，我们在y上加了一个微小值，防止出现np.log(0)的情况，因为np.log(0)会变成负无穷大-inf，从而导致后续的计算无法继续进行。在等式2中\(y_{nk}\)与\(t_{nk}\)下标相同，所以我们直接使用*做element-wise运算，即对应元素相乘。

但当我们希望同时能够处理单个数据和批量数据时，代码块1还不能满足我们的要求。因为当\(N=1\)时，\(y\)是一个包含10个元素的一维向量，输入到函数中，batch_size将等于10而不是1，于是我们将代码块1进行进一步完善，如下：

def cross_entropy_error(y,t):
    if y.ndim == 1:
        y = y.reshape(1,y.size)
        t = t.reshape(1,t.size)

    batch_size = y.shape[0]
    return -np.sum(t * np.log(y + 1e-7)) / batch_size

最后，来讨论一下\(t_{nk}\)为非one-hot表示的情况。在one-hot情况的计算中，t为0的元素cross-entropy error也为0，所以对于这些元素的计算可以忽略。换言之，在非one-hot表示的情况下，我们只需要计算正确解标签的交叉熵误差即可。代码如下：

def cross_entropy_error(y,t):
    if y.ndim == 1:
        y = y.reshape(1,y.size)
        t = t.reshape(1,t.size)

    batch_size = y.shape[0]
    return -np.sum(1 * np.log(y[np.arange(batch_size),t]+1e-7))/batch_size

在上面的代码中，y[np.arange(batch_size),t]表示将从神经网络的输出中抽出与正确解标签相对应的元素。

参考文献

[1] 深度学习入门

[2] DeepLearning.ai深度学习课程笔记

[3] 统计学习方法