数据结构(DataStructure)-03
数据结构-03
数据结构-03笔记
递归
递归定义及特点
【1】定义
递归用一种通俗的话来说就是自己调用自己，但是需要分解它的参数，让它解决一个更小一点的问题，当问题小到一定规模的时候，需要一个递归出口返回 【2】特点
2.1) 递归必须包含一个基本的出口，否则就会无限递归，最终导致栈溢出
2.2) 递归必须包含一个可以分解的问题
2.3) 递归必须必须要向着递归出口靠近
递归示例1
def f(n):
if n == 0:
return
print(n)
f(n-1) f(3)
# 结果: 3 2 1
递归示例2
def f(n):
if n == 0:
return
f(n-1)
print(n) f(3)
# 结果: 1 2 3
递归示例3
# 打印 1+2+3+...+n 的和
def sumn(n):
if n == 1:
return 1
return n + sumn(n-1) print(sumn(3))
递归练习
# 使用递归求出 n 的阶乘
def fac(n):
if n == 1:
return 1
return n * fac(n-1) print(fac(5))
青蛙跳台阶-递归
【1】问题
一共有n级台阶,青蛙一次只能跳一级或两级台阶,问有多少种跳法？
【2】解题思路
定义函数 f(n)
最后一步的跳法有两种(要么最后跳1个台阶到顶部-f(n-1),要么最后跳2个台阶到顶部-f(n-2)) def f(n):
# 递归出口
if n == 1:
return 1
if n == 2:
return 2 return f(n-1) + f(n-2) 思考:如果青蛙一次可以跳一级台阶,二级台阶, 三级台阶 ... n级台阶, n级台阶这个青蛙有多少种跳法？？？
【1】考虑最后一跳的情况
f(n) = f(n-1) + f(n-2) + f(n-3) + ... + f(1)
f(n) = 2f(n-1) 1个台阶: 1
2个台阶: 2
3个台阶: 4
4个台阶: 8
... ... 【2】代码实现
def f(n):
if n == 1:
return 1 return 2 * f(n-1) print(f(4))
递归总结
# 前三条必须记住
【1】递归一定要有出口,一定是先递推,再回归
【2】调用递归之前的语句，从外到内执行，最终回归（打印 3 2 1 的例子)
【3】调用递归或之后的语句，从内到外执行，最终回归（打印 1 2 3 的例子） 【4】Python默认递归深度有限制，当递归深度超过默认值时，就会引发RuntimeError，默认值998
【5】手动设置递归调用深度
import sys
sys.setrecursionlimit(1000000) #表示递归深度为100w
递归动态图解一
递归动态图解二
递归动态图解三
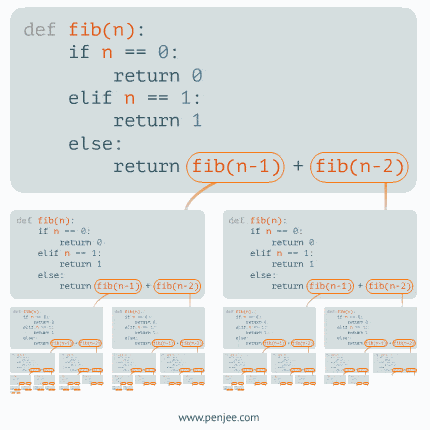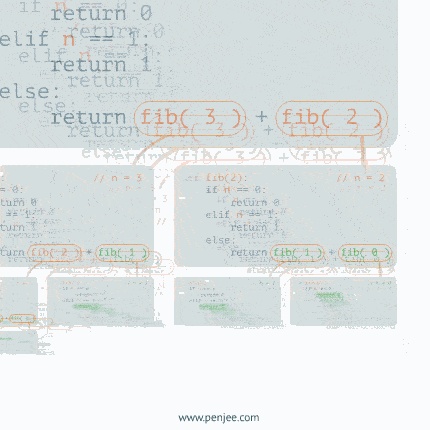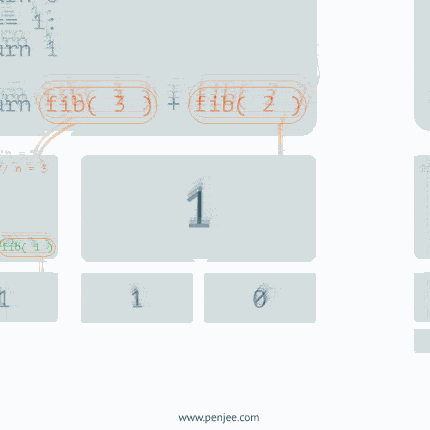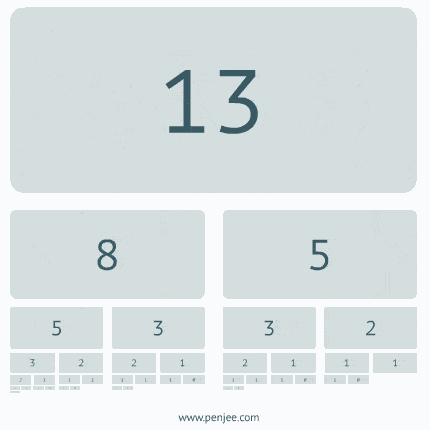
二叉树
定义
二叉树（Binary Tree）是n（n≥0）个节点的有限集合，它或者是空集（n＝0），或者是由一个根节点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成。二叉树与普通有序树不同，二叉树严格区分左孩子和右孩子，即使只有一个子节点也要区分左右
二叉树的分类 - 见图
【1】满二叉树
所有叶节点都在最底层的完全二叉树 【2】完全二叉树
对于一颗二叉树，假设深度为d，除了d层外，其它各层的节点数均已达到最大值，并且第d层所有节点从左向右连续紧密排列 【3】二叉排序树
任何一个节点，所有左边的值都会比此节点小，所有右边的值都会比此节点大 【4】平衡二叉树
当且仅当任何节点的两棵子树的高度差不大于1的二叉树
二叉树 - 添加元素代码实现
"""
二叉树
""" class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None class Tree:
def __init__(self, node=None):
"""创建了一棵空树或者是只有树根的树"""
self.root = node def add(self, value):
"""在树中添加一个节点"""
node = Node(value)
# 空树情况
if self.root is None:
self.root = node
return # 不是空树的情况
node_list = [self.root]
while node_list:
cur = node_list.pop(0)
# 判断左孩子
if cur.left is None:
cur.left = node
return
else:
node_list.append(cur.left) # 判断右孩子
if cur.right is None:
cur.right = node
return
else:
node_list.append(cur.right)
广度遍历 - 二叉树
广度遍历 - 代码实现
def breadth_travel(self):
"""广度遍历 - 队列思想（即：列表的append()方法 和 pop(0) 方法"""
# 1、空树的情况
if self.root is None:
return
# 2、非空树的情况
node_list = [self.root]
while node_list:
cur = node_list.pop(0)
print(cur.value, end=' ')
# 添加左孩子
if cur.left is not None:
node_list.append(cur.left)
# 添加右孩子
if cur.right is not None:
node_list.append(cur.right) print()
深度遍历 - 二叉树
【1】遍历
沿某条搜索路径周游二叉树，对树中的每一个节点访问一次且仅访问一次
【2】遍历方式
2.1) 前序遍历： 先访问树根，再访问左子树，最后访问右子树 - 根 左 右
2.2) 中序遍历： 先访问左子树，再访问树根，最后访问右子树 - 左 根 右
2.3) 后序遍历： 先访问左子树，再访问右子树，最后访问树根 - 左 右 根
【1】前序遍历结果: 1 2 4 8 9 5 10 3 6 7
【2】中序遍历结果: 8 4 9 2 10 5 1 6 3 7
【3】后序遍历结果: 8 9 4 10 5 2 6 7 3 1
深度遍历 - 代码实现
# 前序遍历
def pre_travel(self, node):
"""前序遍历 - 根左右"""
if node is None:
return print(node.value, end=' ')
self.pre_travel(node.left)
self.pre_travel(node.right) # 中序遍历
def mid_travel(self, node):
"""中序遍历 - 左根右"""
if node is None:
return self.mid_travel(node.left)
print(node.value, end=' ')
self.mid_travel(node.right) # 后续遍历
def last_travel(self, node):
"""后序遍历 - 左右根"""
if node is None:
return self.last_travel(node.left)
self.last_travel(node.right)
print(node.value, end=' ')
二叉树完整代码
"""
python实现二叉树
""" class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None class Tree:
def __init__(self, node=None):
"""创建了一棵空树或者是只有树根的树"""
self.root = node def add(self, value):
"""在树中添加一个节点"""
node = Node(value)
# 空树情况
if self.root is None:
self.root = node
return # 不是空树的情况
node_list = [self.root]
while node_list:
cur = node_list.pop(0)
# 判断左孩子
if cur.left is None:
cur.left = node
return
else:
node_list.append(cur.left) # 判断右孩子
if cur.right is None:
cur.right = node
return
else:
node_list.append(cur.right) def breadth_travel(self):
"""广度遍历 - 队列思想（即：列表的append()方法 和 pop(0) 方法"""
# 1、空树的情况
if self.root is None:
return
# 2、非空树的情况
node_list = [self.root]
while node_list:
cur = node_list.pop(0)
print(cur.value, end=' ')
# 添加左孩子
if cur.left is not None:
node_list.append(cur.left)
# 添加右孩子
if cur.right is not None:
node_list.append(cur.right) print() def pre_travel(self, node):
"""前序遍历 - 根左右"""
if node is None:
return print(node.value, end=' ')
self.pre_travel(node.left)
self.pre_travel(node.right) def mid_travel(self, node):
"""中序遍历 - 左根右"""
if node is None:
return self.mid_travel(node.left)
print(node.value, end=' ')
self.mid_travel(node.right) def last_travel(self, node):
"""后序遍历 - 左右根"""
if node is None:
return self.last_travel(node.left)
self.last_travel(node.right)
print(node.value, end=' ') if __name__ == '__main__':
tree = Tree()
tree.add(1)
tree.add(2)
tree.add(3)
tree.add(4)
tree.add(5)
tree.add(6)
tree.add(7)
tree.add(8)
tree.add(9)
tree.add(10)
# 广度遍历：1 2 3 4 5 6 7 8 9 10
tree.breadth_travel()
# 前序遍历：1 2 4 8 9 5 10 3 6 7
tree.pre_travel(tree.root)
print()
# 中序遍历:8 4 9 2 10 5 1 6 3 7
tree.mid_travel(tree.root)
print()
# 后序遍历：8 9 4 10 5 2 6 7 3 1
tree.last_travel(tree.root)
二叉树练习一
题目描述+试题解析
【1】题目描述
从上到下按层打印二叉树，同一层结点从左至右输出，每一层输出一行
1
2 3
4 5 6 7
8 9 10 【2】试题解析
1、广度遍历，利用队列思想
2、要有2个队列，分别存放当前层的节点 和 下一层的节点
代码实现
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None class Solution:
def print_node_layer(self, root):
# 空树情况
if root is None:
return []
# 非空树情况
cur_queue = [root]
next_queue = []
while cur_queue:
cur_node = cur_queue.pop(0)
print(cur_node.value, end=" ")
# 添加左右孩子到下一层队列
if cur_node.left:
next_queue.append(cur_node.left)
if cur_node.right:
next_queue.append(cur_node.right)
# 判断cur_queue是否为空
# 为空：说明cur_queue已经打印完成,并且next_queue已经添加完成,交换变量
if not cur_queue:
cur_queue, next_queue = next_queue, cur_queue
print() if __name__ == '__main__':
s = Solution()
p1 = Node(1)
p2 = Node(2)
p3 = Node(3)
p4 = Node(4)
p5 = Node(5)
p6 = Node(6)
p7 = Node(7)
p8 = Node(8)
p9 = Node(9)
p10 = Node(10)
p1.left = p2
p1.right = p3
p2.left = p4
p2.right = p5
p3.left = p6
p3.right = p7
p4.left = p8
p4.right = p9
p5.left = p10
s.print_node_layer(p1)
二叉树练习二
题目描述+试题解析
【1】题目描述
请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印， 第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推
1
3 2
4 5 6 7
10 9 8 【2】试题解析
1、采用层次遍历的思想，用队列或者栈（先进先出或后进先出，此处二选一，我们选择栈）
2、把每一层的节点添加到一个栈中，添加时判断是奇数层还是偶数层
a) 奇数层：栈中存储时，二叉树中节点从右向左append，出栈时pop()则从左向右打印输出
b) 偶数层: 栈中存储时，二叉树中节点从左向右append，出栈时pop()则从右向左打印输出
代码实现
"""
请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印， 第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推
思路：
1、选择一种数据结构来解决问题 - 栈（LIFO后进先出） - 顺序表（append() 和 pop()）
2、通过观察,发现了规律：
2.1) 当前操作为奇数层时：先左后右 添加到下一层
2.2) 当前操作为偶数层时：先右后左 添加到下一层
"""
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None class Solution:
def print_node_zhi(self, root):
# 空树情况
if root is None:
return []
# 非空树情况 - 栈思想（后进先出）
cur_stack = [root]
next_stack = []
level = 1
while cur_stack:
cur_node = cur_stack.pop()
print(cur_node.value, end=" ")
# 添加左右孩子 - 当前层为奇数层从左至右,当前层为偶数层从右至左
if level % 2 == 1:
if cur_node.left:
next_stack.append(cur_node.left)
if cur_node.right:
next_stack.append(cur_node.right)
else:
if cur_node.right:
next_stack.append(cur_node.right)
if cur_node.left:
next_stack.append(cur_node.left) # 交换变量
if not cur_stack:
cur_stack, next_stack = next_stack, cur_stack
level += 1
print() if __name__ == '__main__':
s = Solution()
p1 = Node(1)
p2 = Node(2)
p3 = Node(3)
p4 = Node(4)
p5 = Node(5)
p6 = Node(6)
p7 = Node(7)
p8 = Node(8)
p9 = Node(9)
p10 = Node(10)
p1.left = p2
p1.right = p3
p2.left = p4
p2.right = p5
p3.left = p6
p3.right = p7
p4.left = p8
p4.right = p9
p5.left = p10
s.print_node_zhi(p1)
二叉排序树练习一
题目描述+试题解析【1】题目描述
给定一棵二叉搜索树，请找出其中的第 K 小的结点。例如，(5,3,7,2,4,6,8)中， 按结点数值大小顺序第三小结点的值是 4 【2】试题解析
1、二叉搜索树定义及特点
a> 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
b> 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
c> 它的左、右子树也分别为二叉排序树
2、二叉搜索树的中序遍历是递增的序列，利用中序遍历来解决
- 二叉搜索树示例
代码实现
class TreeNode:
def __init__(self,value):
self.value = value
self.left = None
self.right = None class Solution:
def __init__(self):
self.result = [] def get_k_node(self,root,k):
array_list = self.inorder_travel(root)
if k <= 0 or len(array_list) < k:
return None
return array_list[k-1] def inorder_travel(self,root):
if root is None:
return self.inorder_travel(root.left)
self.result.append(root.value)
self.inorder_travel(root.right) return self.result if __name__ == '__main__':
s = Solution()
t12 = TreeNode(12)
t5 = TreeNode(5)
t18 = TreeNode(18)
t2 = TreeNode(2)
t9 = TreeNode(9)
t15 = TreeNode(15)
t19 = TreeNode(19)
t17 = TreeNode(17)
t16 = TreeNode(16)
# 开始创建树
t12.left = t5
t12.right = t18
t5.left = t2
t5.right = t9
t18.left = t15
t18.right = t19
t15.right = t17
t17.left = t16 print(s.inorder_travel(t12))
print(s.get_k_node(t12,3))
二叉排序树练习二
题目描述+试题解析
【1】题目描述
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中节点指针的指向 【2】试题解析
a> 二叉搜索树的中序遍历是一个不减的排序结果，因此先将二叉树搜索树中序遍历
b> 将遍历后的结果用相应的指针连接起来
二叉搜索树示例
代码实现
class TreeNode:
def __init__(self,value):
self.value = value
self.left = None
self.right = None class Solution:
def __init__(self):
self.result = [] def convert_tree_link(self,root):
array_list = self.inner_travel(root)
if len(array_list) == 0:
return None
if len(array_list) == 1:
return root # 先把头节点和尾节点搞定
array_list[0].left = None
array_list[0].right = array_list[1]
array_list[-1].left = array_list[-2]
array_list[-1].right = None
# 搞定中间节点
for i in range(1,len(array_list)-1):
array_list[i].left = array_list[i-1]
array_list[i].right = array_list[i+1] return array_list[0] def inner_travel(self,root):
if root is None:
return self.inner_travel(root.left)
self.result.append(root)
self.inner_travel(root.right) return self.result if __name__ == '__main__':
s = Solution()
t12 = TreeNode(12)
t5 = TreeNode(5)
t18 = TreeNode(18)
t2 = TreeNode(2)
t9 = TreeNode(9)
t15 = TreeNode(15)
t19 = TreeNode(19)
t17 = TreeNode(17)
t16 = TreeNode(16)
# 开始创建树
t12.left = t5
t12.right = t18
t5.left = t2
t5.right = t9
t18.left = t15
t18.right = t19
t15.right = t17
t17.left = t16 head_node = s.convert_tree_link(t12)
# 打印双向链表的头节点：2
print(head_node.value)
# 从头到尾打印双向链表的节点
while head_node:
print(head_node.value,end=" ")
head_node = head_node.right print()
冒泡排序
排序方式
# 排序方式
遍历列表并比较相邻的元素对，如果元素顺序错误，则交换它们。重复遍历列表未排序部分的元素，直到完成列表排序 # 时间复杂度
因为冒泡排序重复地通过列表的未排序部分，所以它具有最坏的情况复杂度O(n^2)
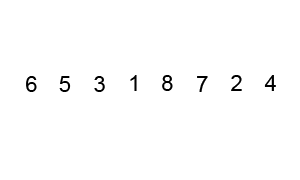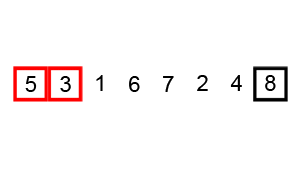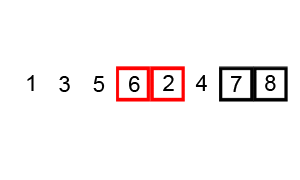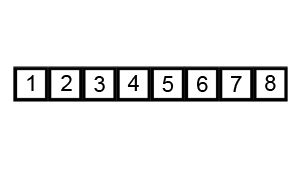
代码实现
"""
冒泡排序
3 8 2 5 1 4 6 7
"""
def bubble_sort(li):
# 代码第2步: 如果不知道循环几次，则举几个示例来判断
for j in range(0,len(li)-1):
# 代码第1步: 此代码为一波比对，此段代码一定一直循环，一直比对多次至排序完成
for i in range(0,len(li)-j-1):
if li[i] > li[i+1]:
li[i],li[i+1] = li[i+1],li[i] return li li = [3,8,2,5,1,4,6,7]
print(bubble_sort(li))
归并排序
排序规则
# 思想
分而治之算法 # 步骤
1) 连续划分未排序列表，直到有N个子列表，其中每个子列表有1个"未排序"元素，N是原始数组中的元素数
2) 重复合并，即一次将两个子列表合并在一起，生成新的排序子列表，直到所有元素完全合并到一个排序数组中
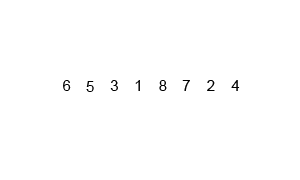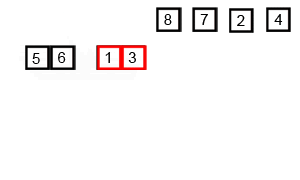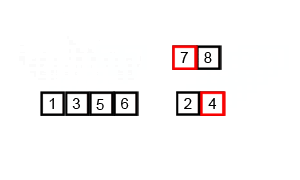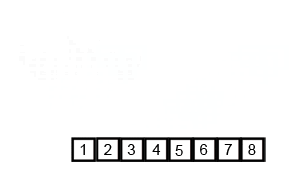
代码实现 - 归并排序
"""
归并排序
""" def merge_sort(li):
# 递归出口
if len(li) == 1:
return li # 第1步：先分
mid = len(li) // 2
left = li[:mid]
right = li[mid:]
# left_li、right_li 为每层合并后的结果,从内到外
left_li = merge_sort(left)
right_li = merge_sort(right) # 第2步：再合
return merge(left_li,right_li) # 具体合并的函数
def merge(left_li,right_li):
result = []
while len(left_li)>0 and len(right_li)>0:
if left_li[0] <= right_li[0]:
result.append(left_li.pop(0))
else:
result.append(right_li.pop(0))
# 循环结束,一定有一个列表为空,将剩余的列表元素和result拼接到一起
result += left_li
result += right_li return result if __name__ == '__main__':
li = [1,8,3,5,4,6,7,2]
print(merge_sort(li))
快速排序
排序规则
【1】介绍
快速排序也是一种分而治之的算法，在大多数标准实现中，它的执行速度明显快于归并排序 【2】排序步骤：
2.1) 首先选择一个元素，称为数组的基准元素
2.2) 将所有小于基准元素的元素移动到基准元素的左侧；将所有大于基准元素的移动到基准元素的右侧
2.3) 递归地将上述两个步骤分别应用于比上一个基准元素值更小和更大的元素的每个子数组
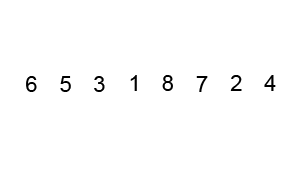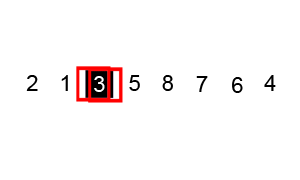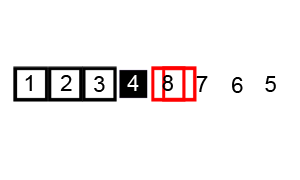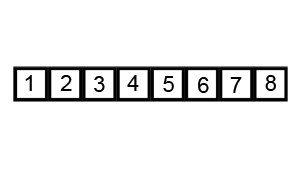
代码实现 - 快速排序
"""
快速排序
1、left找比基准值大的暂停
2、right找比基准值小的暂停
3、交换位置
4、当right<left时，即为基准值的正确位置，最终进行交换
"""
def quick_sort(li, first, last):
if first > last:
return # 找到基准值的正确位置下表索引
split_pos = part(li, first, last)
# 递归思想,因为基准值正确位置左侧继续快排,基准值正确位置的右侧继续快排
quick_sort(li, first, split_pos-1)
quick_sort(li, split_pos+1, last) def part(li, first, last):
"""找到基准值的正确位置,返回下标索引"""
# 基准值、左游标、右游标
mid = li[first]
lcursor = first + 1
rcursor = last
sign = False
while not sign:
# 左游标右移 - 遇到比基准值大的停
while lcursor <= rcursor and li[lcursor] <= mid:
lcursor += 1
# 右游标左移 - 遇到比基准值小的停
while lcursor <= rcursor and li[rcursor] >= mid:
rcursor -= 1
# 当左游标 > 右游标时,我们已经找到了基准值的正确位置,不能再移动了
if lcursor > rcursor:
sign = True
# 基准值和右游标交换值
li[first],li[rcursor] = li[rcursor],li[first]
else:
# 左右游标互相交换值
li[lcursor],li[rcursor] = li[rcursor],li[lcursor] return rcursor if __name__ == '__main__':
li = [6,5,3,1,8,7,2,4,6,5,3]
quick_sort(li, 0, len(li)-1) print(li)
二分查找
定义及规则
【1】定义及优点
二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好 【2】查找过程
二分查找即搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果中间元素大于或小于要查找元素,则在小于或大于中间元素的那一半进行搜索,而且跟开始一样从中间元素开始比较. 如果在某一步骤数组为空,则代表找不到.这种算法每一次比较都会使搜索范围缩小一半. 【3】适用条件
数组必须有序
二分查找图解一
- 二分查找图解二
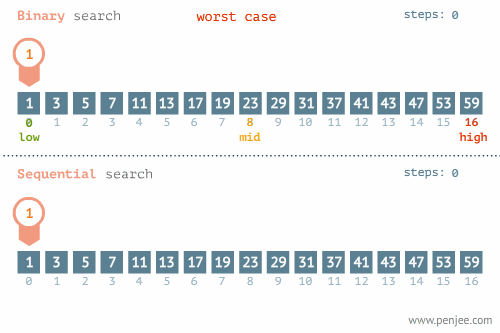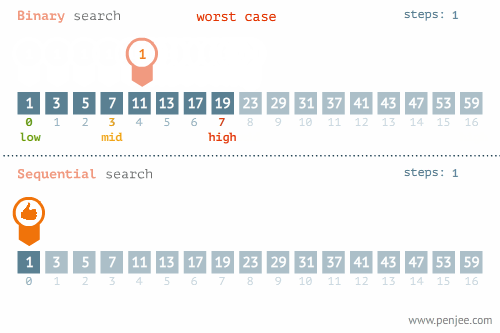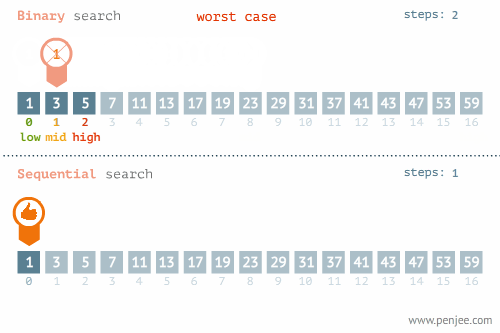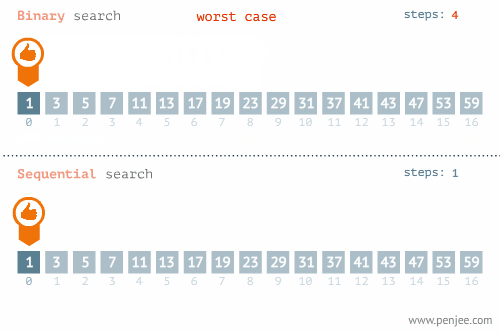
代码实现
def binary_search(alist, item):
"""
二分查找
"""
n = len(alist)
first = 0
last = n - 1
while first <= last:
mid = (last+first)//2
if alist[mid] > item:
last = mid - 1
elif alist[mid] < item:
first = mid + 1
else:
return True
return False if __name__ == "__main__":
lis = [2, 4, 5, 12, 14, 23]
if binary_search(lis, 12):
print('ok')
else:
print('false')
数据结构(DataStructure)-03的更多相关文章
- 数据结构(DataStructure)与算法(Algorithm)、STL应用
catalogue . 引论 . 数据结构的概念 . 逻辑结构实例 2.1 堆栈 2.2 队列 2.3 树形结构 二叉树 . 物理结构实例 3.1 链表 单向线性链表 单向循环链表 双向线性链表 双向 ...
- 20160203.CCPP体系详解(0013天)
程序片段(01):数组.c+02.数组初始化语法.c 内容概要:数组 ///01.数组.c #include <stdio.h> #include <stdlib.h> //0 ...
- 11.python3标准库--使用进程、线程和协程提供并发性
''' python提供了一些复杂的工具用于管理使用进程和线程的并发操作. 通过应用这些计数,使用这些模块并发地运行作业的各个部分,即便是一些相当简单的程序也可以更快的运行 subprocess提供了 ...
- BUAA OO 2019 第三单元作业总结
目录 总 JML规格化设计 理论基础 工具链 规格验证 验证代码 代码静态检查 自动生成测试样例 生成结果 错误分析 作业设计 第九次作业 架构 代码实现 第十次作业 架构 代码实现 第十一次作业 架 ...
- 搞大数据，Java 工程师需要掌握哪些知识？
先看再点赞,给自己一点思考的时间,微信搜索[沉默王二]关注这个有颜值却假装靠才华苟且的程序员.本文 GitHub github.com/itwanger 已收录,里面还有一线大厂整理的面试题,以及我的 ...
- 《Head First 设计模式》：剩下的模式
正文 一.桥接模式 1.定义 桥接模式通过将实现和抽象分离开来,放在两个不同的类层次中,从而使得它们可以独立改变. 要点: 当一个类存在两个独立变化的维度,而且都需要进行扩展时,可以将其中一个维度抽象 ...
- Clojure学习03：数据结构（集合）
Clojure提供了几种强大的数据结构(集合) 一.集合种类 1.vector 相当于数组,如: [2 3 5] , ["ad" "adas" & ...
- 用js来实现那些数据结构（数组篇03）
终于,这是有关于数组的最后一篇,下一篇会真真切切给大家带来数据结构在js中的实现方式.那么这篇文章还是得啰嗦一下数组的相关知识,因为数组真的太重要了!不要怀疑数组在JS中的重要性与实用性.这篇文章分为 ...
- 03.DataStructure
01.list ''' list 특징 - 1차원 배열 구조 형식) 변수 = [값1, 값2] - 다양한 자료형 저장 가능 - index 사용=순서 존재 형식) 변수[n] - 값 수정( ...
- 用js来实现那些数据结构03（数组篇03-排序及多维数组）
终于,这是有关于数组的最后一篇,下一篇会真真切切给大家带来数据结构在js中的实现方式.那么这篇文章还是得啰嗦一下数组的相关知识,因为数组真的太重要了!不要怀疑数组在JS中的重要性与实用性.这篇文章分为 ...
随机推荐
- 9.6 2020 实验 1：Mininet 源码安装和可视化拓扑工具
一.实验目的 掌握 Mininet 的源码安装方法和 miniedit 可视化拓扑生成工具. 二.实验任务 使用源码安装 Mininet 的 2.3.0d6 版本,并使用可视化拓扑工具生成一个最简 ...
- linux 部署轻量级堡垒机Next Terminal
对比 类似的开源堡垒机有 Teleport,Jumpserver,Next Terminal等等. Teleport 安全性最好,较轻量,但是对被管理资产不透明,纳管前需要双向认证,在资产设备上需额外 ...
- PHP接受json数据
PHP接受json数据 获取请求的参数 $input = file_get_contents("php://input"); $input = json_decode($input ...
- ACE Editor 常用Api（转）
ACE 是一个开源的.独立的.基于浏览器的代码编辑器,可以嵌入到任何web页面或JavaScript应用程序中.ACE支持超过60种语言语法高亮,并能够处理代码多达400万行的大型文档.ACE开发团队 ...
- 几种C#实现播放声音的方法 DirectX、SoundPlayer等
第一种是利用DirectX 1.安装了DirectX SDK(有9个DLL文件).这里我们只用到MicroSoft.DirectX.dll 和 Microsoft.Directx.DirectSou ...
- 线程Thread小记
1 public class ConcurentDemo extends Thread { 2 @Override 3 public void run() { 4 super.run(); 5 Sys ...
- (转载)Python 浅析线程（threading模块）和进程（process）
线程是操作系统能够进行运算调度的最小单位.它被包含在进程之中,是进程中的实际运作单位.一条线程指的是进程中一个单一顺序的控制流,一个进程中可以并发多个线程,每条线程并行执行不同的任务 进程与线程 什么 ...
- Python：合并两个列表成为一个list
如何合并两个列表,今天就来探讨一下: 方法一:最笨的方法实现 list1=[1,2,3]list2=[4,5,6]new_list=[]for item in list1: new_list.appe ...
- echart 解决setOption线残留
前言: Antd + echarts 我想要实现的是点击表的某一行自动生成对应的折线图,我在点击第一行生成5条线,我在点击第二行的时候,本该生成2条线,结果还是5条线: 最开始我以为设置的 serie ...
- SpringCloud微服务实战——搭建企业级开发框架（五十一）：微服务安全加固—自定义Gateway拦截器实现防止SQL注入/XSS攻击
SQL注入是常见的系统安全问题之一,用户通过特定方式向系统发送SQL脚本,可直接自定义操作系统数据库,如果系统没有对SQL注入进行拦截,那么用户甚至可以直接对数据库进行增删改查等操作. XSS ...