CSP2022 J2参考解析

P8813 [CSP-J2022] 乘方
P8814 [CSP-J2022] 解密
P8815 [CSP-J2022] 逻辑表达式
P8816 [CSP-J2022] 上升点列

题目传送：

P8813 [CSP-J2022] 乘方

题目描述很简单，但是数据范围很大, $a,b \in [1,10^9]$。
方法1：一眼 long long 快速幂，可AC，但是有一个细节
快速幂可能存在情况 ans 合理，ans*a 越界到 $[1,10^9]$，这个坑需要注意。
方法2：细想一下 $2^{31}>1e9$，其实直接暴力枚举就行，特判 $a=1$的情况。

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N=1e6+10,INF=0x3f3f3f3f, M=1e9;

LL fpow(LL a,LL n){

    for(int i=1; i<=n && i<32; i++){

        if((LL)pow(a,i)>M) return -1;

    } // 提前处理

    LL ans=1;

    while(n){

        if(n&1) ans=ans*a;

        if(ans>M || a>=M) return -1;

        a = a*a;

        n>>=1;

    }

    return ans;

}

LL slove2(LL a,LL n){

    if(a==1) return 1;

    LL ans=1;

    for(int i=1; i<=n && i<32; i++){

        ans = ans*a;

        if(ans > M) return -1;

    }

    return ans;

}

int main(){

    LL a,b;

    while(cin>>a>>b){

//        cout<<fpow(a,b)<<endl;

        cout<<slove2(a,b)<<endl;

    }

    fclose(stdin); fclose(stdout); return 0;

}

P8814 [CSP-J2022] 解密

题意：$p*q=n, e*d=(p-1)(q-1)+1$，已知 $n,e,d$，求 $p,q$。
明显可以用一元二次方程 $O(1)$ 解
一元二次方程：$ax^2+bx+c=0$，已知 $a,b,c$，求解 $x$。
公式：$\Delta=b^2-4ac$
如果 $\Delta < 0$，则无解。
如果 $\Delta=0$，则有唯一解 $x=\frac{-b}{2a}$
如果 $\Delta>0$，则有两个不同的解 $x=\frac{-b±\sqrt{\Delta}}{2a}$
推导

\[\begin{aligned}
&e*d = p*q - (p+q) + 2\\
&p + q = n-e*d+2 = m \\
&p*q = p * (m- p) = n，结合上述方程，代入可得如下方程： \\ \\
&p^2 - m*p + n = 0 // 解此方程，求出 p \\
&\Delta = (-m)^2 - 4*1 *n = m^2 -4n \\
\\
&if(\Delta < 0) // NO 无解 \\
&else\{ \\
&\quad p = (m^2 ± \sqrt{\Delta})/2 \\
&\quad q = n/p \\
&\quad if(p > q) swap(p,q); \\
&\quad if(p*q==n \&\& p+q==m) // p q 就是答案 \\
&\quad else // NO 无解 \\
&\} \\
&\end{aligned}
\]

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N=1e6+10,INF=0x3f3f3f3f, M=1e9;

LL k,n,e,d;

int main() {

//    freopen("data.in", "r", stdin);

    cin>>k;

    for(int i=1; i<=k; i++) {

        cin>>n>>e>>d;

        LL m = n+2-e*d;

        LL delta = m*m - 4*n;

        if(delta < 0) cout<<"NO"<<endl;

        else {

            LL p = (m-(LL)sqrt(delta)) /2;

            LL q = n/p;

            // if(p > q) swap(p, q);

            if(p*q==n && p+q==m) cout<<p<<" "<<q<<endl;

            else cout<<"NO"<<endl;

        }

    }

    fclose(stdin); fclose(stdout); return 0;

}

上述 $O(1)$ 的说法其实不是那么准确，可以说是 $O(\sqrt{n})$，主要在开方的时候，其复杂度一般是和牛顿迭代法相当的，比二分要优秀。
sqrt() 复杂度介绍
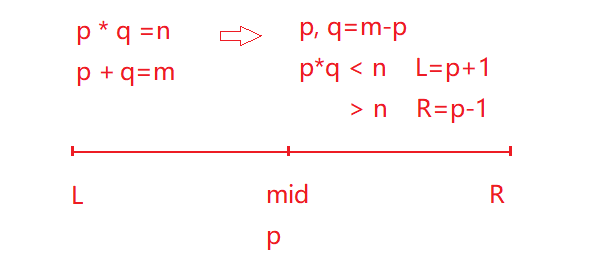
方法2：二分答案 $p$，单次复杂度 $O(logn)$，可以AC
$p*q=n, p+q=m$
二分性质：两个正整数的和一定，那么差越小，乘积越大。

\[\begin{aligned}
&证明：令 a+b = n, a-b = m，\\
&则 a = \frac{n+m}{2}, b=\frac{n-m}{2},\\
&a*b = \frac{(n+m)*(n-m)}{2} = \frac{n^2-m^2}{2} \\
&由于 n是固定的，所以 m越小，a*b越大。
\end{aligned}
\]

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N=1e6+10,INF=0x3f3f3f3f, M=1e9;

LL k,n,e,d;

int main() {

//    freopen("data.in", "r", stdin);

    cin>>k;

    for(int i=1; i<=k; i++) {

        cin>>n>>e>>d;

        LL m = n+2-e*d;

        LL l=1, r=m-1, p, q, flag=0;

        while(l<=r) {

            p = l+r>>1, q = m-p;

            if(p*q==n) {

                if(p>q) swap(p, q);

                cout<<p<<" "<<q<<endl;

                flag=1; break;

            } else if(p*q<n) {

                l = p+1;

            } else {

                r = p-1;

            }

        }

        if(!flag) cout<<"NO"<<endl;

    }

    fclose(stdin); fclose(stdout); return 0;

}

P8815 [CSP-J2022] 逻辑表达式

大模拟，表达式树，栈
这和表达式求值的题目比较相似，只是计算对象变为三元组，确定优先级
另外就是计算的一些规则需要重新推导一下，如下图

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N=1e6+10,INF=0x3f3f3f3f, M=1e9;

unordered_map<char,int> pr {{'&', 2}, {'|', 1}};

/*

 (v,a,b)  = (value, and, or)

 (1,a1,b1) & (v,a2,b2) = (v, a1+a2, b1+b2)

 (0,a1,b1) | (v,a2,b2) = (v, a1+a2, b1+b2)

 (0,a1,b1) & (v,a2,b2) = (0, a1+1, b1)

 (1,a1,b1) | (v,a2,b2) = (1, a1, b1+1)

*/

struct T {

    int v,a,b;

} pa,pb;

stack<T> num;

stack<char> op;

void cal() {

    pb=num.top(), num.pop();

    pa=num.top(), num.pop();

    char c = op.top(); op.pop();

    int a1=pa.a, b1=pa.b, v=pb.v, a2=pb.a, b2=pb.b;

    if(c=='&') {

        // (0,a1,b1) & (v,a2,b2) = (0,a1+1,b1)

        // (1,a1,b1) & (v,a2,b2) = (v,a1+a2,b1+b2)

        if(pa.v==0) num.push({0,a1+1,b1});

        else num.push({v,a1+a2,b1+b2});

    } else if(c=='|') {

        // (0,a1,b1) | (v,a2,b2) = (v,a1+a2,b1+b2)

        // (1,a1,b1) | (v,a2,b2) = (1,a1,b1+1)

        if(pa.v==0) num.push({v,a1+a2,b1+b2});

        else num.push({1,a1,b1+1});

    }

}

int main() {

//    freopen("data.in", "r", stdin);

    string s;

    while(cin>>s) {

//        while(num.size()) num.pop();

//        while(op.size()) op.pop();

        for(int i=0; i<s.size(); i++) {

            char c = s[i];

            if(isdigit(c)) num.push({c-'0', 0, 0});

            else if(c=='(') {

                op.push(c);

            } else if(c==')') {

                while(op.top()!='(') cal();

                op.pop();

            } else {

                while(op.size() && op.top()!=')' &&

                        pr[op.top()] >= pr[c]) cal();

                op.push(c);

            }

        }

        while(op.size()) cal();

        cout<<num.top().v<<endl;

        cout<<num.top().a<<" "<<num.top().b<<endl;

    }

    fclose(stdin); fclose(stdout); return 0;

}

P8816 [CSP-J2022] 上升点列

最长上升子序列，二维DP
状态：$f_{i,j}$ 表示以第 $i$ 个元素结尾，插入 $j$ 个元素的最长上升序列长度。
转移：$f_{i,j}=max\{f_{i,j-d}+d+1\} ,d = x2-x1+y2-y1-1$
目标：$ans=max\{f_{i,k}\}$

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N=510,INF=0x3f3f3f3f;

int n,k,f[N][N],ans=0;

struct T{

    int x,y;

    bool operator< (const T& rhs) const{

        if(x!=rhs.x) return x<rhs.x;

        return y<rhs.y;

    }

}g[N];

// 状态：f[i][j] 表示序列以i结尾，添加j个点序列的最大长度

// 转移：f[i][j] = max(f[i][j], f[t][j-d]+d+1)

// d = x2-x1+y2-y1-1

int main(){

    cin>>n>>k; int x,y;

    for(int i=1; i<=n; i++) { cin>>x>>y; g[i]={x,y}; }

    sort(g+1, g+1+n);

    for(int i=1; i<=n; i++){

        for(int j=0; j<=k; j++){

            f[i][j]=j+1;

            for(int t=1; t<i; t++){ // t -> i

                if(g[t].x > g[i].x || g[t].y > g[i].y) continue;

                int d=g[i].x-g[t].x+g[i].y-g[t].y-1;

                if(j>=d) f[i][j]=max(f[i][j], f[t][j-d]+d+1);

            }

        }

    }

    for(int i=1; i<=n; i++) ans=max(ans,f[i][k]);

    cout<<ans;

    fclose(stdin); fclose(stdout); return 0;

}