JZOJ 3234. 阴阳

阴阳

题面

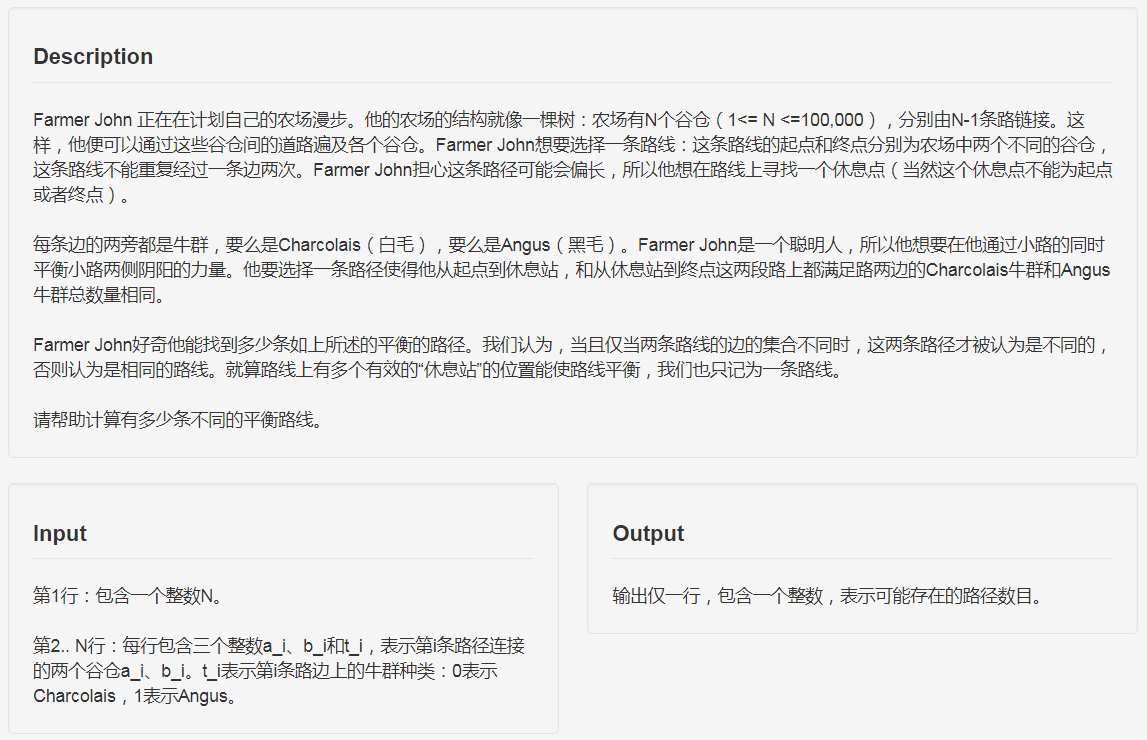
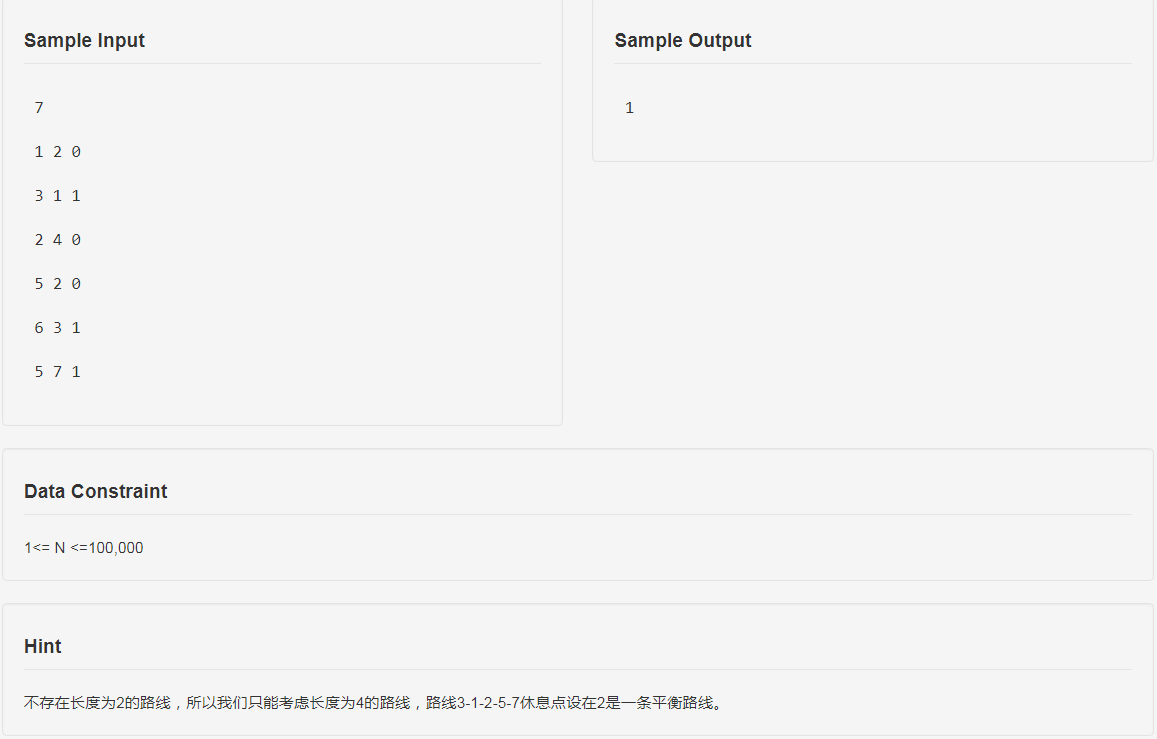
分析

个人认为是极好的题，很容易写

如果你学点分治是无奈背板的，那就做做这道题，加深你对点分治的理解

一般的，处理树上大规模统计问题，我们分治的关键是找一棵子树的重心

找到分治中心，即新一轮的根节点，然后处理子树节点经过根节点时的答案，接着对子树继续分治下去

那么我们看这题，让黑白的各自变为 \(1\) 或 \(-1\)

合法的路径是这样的：能找到一个分割点使路径两端各自的和分别为 \(0\)

那么我们思考在统计经过根节点的答案时，只有不同子树的两路径合并时或一棵子树中某节点到根距离为 \(0\) 且其路径上有分割点才可能产生答案

也就是说，我们要找的路径和必须为 \(0\) 且有分割点

找路径和为 \(0\) 很简单，记录子树节点到根的距离 \(dis\)（可能为负，所以让他加上 \(n\) 避免出错），两路径合并时，设其两端为 \(x,y\)，\(dis[x]+dis[y] = 0\) 是必要条件

重点就是如何判断两路径是否有分割点，是的话我们就可以统计答案

那么我们回到 \(dis[x]+dis[y] = 0\) 这句话

\(dis[y]=-dis[x]\)，若 \(dis[y]\) 他到根节点中 值是非第一次出现的，那么可以直接贡献答案

我们只需要记下这类点的个数就好了，即开桶以值为下标记个数，我们称其为二类桶

？？？那一类桶呢？

既然二类桶是非第一次出现，那一类桶就记第一次出现的个数

我们可以用 \(flag[x]=1\) 表示 \(dis[x]\) 已经出现过

因为是遍历子树是深搜的顺序，所以我们再开个桶标记在他到根节点路径中 \(dis\) 出现的次数，这样就可以很好的判断 \(flag\) 是否需要标记为 \(1\)

那么考虑当前节点如何计算答案

• 若他的 \(dis\) 到根节点是第一次出现，那么他可以直接加上二类桶。注意 \(dis\) 为 \(0\) 的话他又可以加一类桶，因为此时的根可以为路径的分割点
• 若他的 \(dis\) 到根节点不是第一次出现，那么他可以加上一、二类桶，因为他先前的 \(dis\) 到他的距离为 \(0\)，即先前的 \(dis\) 可做分割点。当然，此时他 \(dis\) 若为 \(0\) 同理说明他到根也是合法路径，所以答案加 \(1\)。记得标记当前点的 \(flag\) 为 \(1\)
  
  每次统计完一个子树，就要再遍历一遍这个子树更新一类、二类桶的信息

换重心时我们不能直接把数组清 \(0\)，为了保证复杂度，我们统计完所有子树的答案后再遍历一遍所有子树，将一类、二类桶的信息退回，\(flag\) 和 \(dis\) 清 \(0\)

完结撒花

\(Code\)

#include<cstdio>
#include<iostream>
using namespace std;
typedef long long LL;

const int N = 1e5 + 5;
int n , buc[N << 1] , buc1[N << 1][3] , flag[N] , dis[N] , h[N] , size , siz[N] , son[N] , rt , use[N] , tot;
LL ans; 

struct edge{
	int to , nxt , w;
}e[2 * N];

inline void add(int x , int y , int z)
{
	e[++tot].nxt = h[x];
	e[tot].to = y;
	e[tot].w = z;
	h[x] = tot;
}

inline void getrt(int x , int fa)
{
	son[x] = 0 , siz[x] = 1;
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa || use[v]) continue;
		getrt(v , x);
		siz[x] += siz[v];
		son[x] = max(son[x] , siz[v]);
	}
	son[x] = max(son[x] , size - siz[x]);
	rt = son[x] < son[rt] ? x : rt;
}

inline void getdis(int x , int fa)
{
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa || use[v]) continue;
		dis[v] = dis[x] + e[i].w;
		getdis(v , x);
	}
}

inline void fill(int x , int fa)
{
	++buc1[dis[x] + n][flag[x]];
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa || use[v]) continue;
		fill(v , x);
	}
}

inline void clear(int x , int fa)
{
	--buc1[dis[x] + n][flag[x]];
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa || use[v]) continue;
		clear(v , x);
	}
	dis[x] = flag[x] = 0;
}

inline LL dfs(int x , int fa)
{
	LL res = 0;
	if (buc[dis[x] + n]) flag[x] = 1 , res += buc1[-dis[x] + n][0] + buc1[-dis[x] + n][1] + (!dis[x] ? 1 : 0);
	else{
		if (!dis[x]) res += buc1[-dis[x] + n][0];
		res += buc1[-dis[x] + n][1];
	}
	++buc[dis[x] + n];

	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa || use[v]) continue;
		res += dfs(v , x);
	}
	--buc[dis[x] + n];
	return res;
}

inline LL calc(int x)
{
	getdis(x , 0);
	LL res = 0;
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (use[v]) continue;
		res += dfs(v , x);
		fill(v , x);
	}
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (use[v]) continue;
		clear(v , x);
	}
	return res;
}

inline void divide(int x)
{
	use[x] = 1 , ans += calc(x);
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (use[v]) continue;
		size = siz[v] , rt = 0;
		getrt(v , x) , divide(rt);
	}
}

int main()
{
	scanf("%d" , &n);
	int u , v , w;
	for(register int i = 1; i < n; i++)
	{
		scanf("%d%d%d" , &u , &v , &w);
		w = w ? 1 : -1;
		add(u , v , w) , add(v , u , w);
	}
	son[0] = 2e9 , size = n;
	getrt(1 , 0) , divide(rt);
	printf("%lld" , ans);
}