投资组合计算分析—

“投资组合”是指金融资产（如股票、债券和现金）的任何组合。投资组合有很多类型，包括市场投资组合和零投资投资组合。可以使用以下任何一种投资方法和原则来管理投资组合的资产分配：股息加权、均等加权、资本化加权、价格加权、风险平价、资本资产定价模型、套利定价理论、詹森指数、特雷诺比率、夏普对角线（或指数）模型、风险价值模型、现代投资组合理论等。

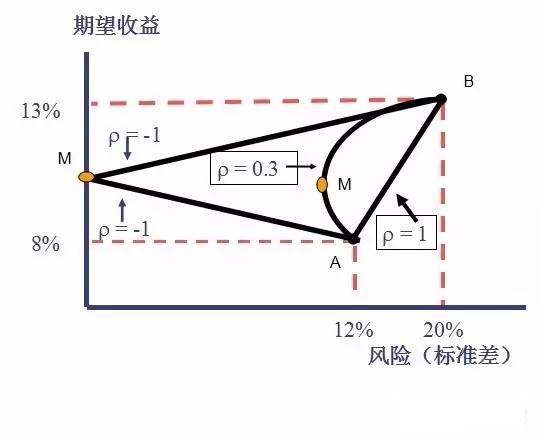
一、投资组合理论

投资组合理论是指若干种证券组成的投资组合，其收益是这些证券收益的加权平均数，但是其风险不是这些证券风险的加权平均风险，投资组合能降低非系统性风险。美国经济学家马考维茨于1952年首次提出投资组合理论，并进行了系统、深入和卓有成效的研究。

1.1 收益与风险

收益很好理解，咱们主要看什么是风险。在金融学中，风险是指不确定性。比如说，你买了1年期的国债，约定收益是5%，那么1年后你必定会获得回报5%，既不会多一点，也不会少一点，这种投资就是无风险的。再比如，你通过长期统计发现，股票的长期平均收益是10%，但回报非常不稳定。碰到好的年份，回报可能是50%，碰到不好的年份，回报可能是-30%。这10%的收益，并不是一定能拿到的，具有不确定性，这就是风险。对于有风险的投资来说，最终的收益是随机的。上例中的10%叫做期望收益，是指经过多次投资之后，平均意义上的收益。

在投资学里，常用标准差来度量不确定。标准差越大，则表示不确定性越大，最终的收益越有可能偏离期望收益。最常见的随机分布就是正态分布，也叫高斯分布，对于正态分布标准差小的更集中一些，标准差大的更为分散。也就是说标准差越小，不确定性越小；反之，标准差越大，不确定性越大。

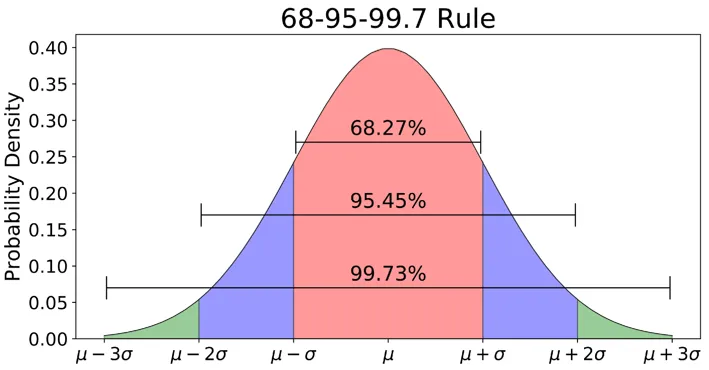
对于上图的高斯正态分布，一次抽样落入1倍标准差内的概率是68%，落入2倍标准差内的概率是95%，落入3倍标准差内的概率是99.7%。比如说，某个投资品种回报服从高斯分布，期望收益为10%，标准差为5%。那么就可以说，最终回报在5%到15%的概率为68%，亏损的概率(低于2倍标准差)为2.5%，亏损5%以上的概率(低于3倍标准差)为0.15%。经济学理论中，假设人都是理性的。也就是说，人们都愿意获得高收益，但不愿意承担高风险。面对风险相同的投资品种，人们选择收益高的。面对收益相同的投资品种，人们选择风险低的。

1.2马科维茨投资组合理论

分析多项风险资产构成的资产组合（portfolio）的基本方法是马科维茨（Markowitz）模型，其遵循7个基本假设

投资者遵循效用最大化原则；
投资期为一期；
投资者是风险回避者，即在收益相等的条件下，投资者选择风险最低的投资组合；
投资者根据均值、方差以及协方差来选择最佳投资组合；
证券市场是完善的，无交易成本，而且证券可以无限细分；
资金全部用于投资，但不允许卖空；
证券间的相关系数都不是-1，不存在无风险证券，而且至少有两个个证券的预期收益是不同的；

一般来说，投资组合的预期收益率（期望）的计算方法为：

\[E(Rp)=\sum_{i=1}^{N}{W_{i}E(R_{i})}
\]

其中：$R_p$为资产组合的收益期望;$R_i$为单个资产的收益期望;$W_i$为第i个资产的仓位（投资比例）,也就是各项资产的收益率期望的加权平均（如A资产收益率期望为10%，占60%仓位；B资产收益率期望为5%，占40%仓位，则投资组合的期望收益率为 10% x 60% + 5% x 40% = 8%)。

我们投资不仅关注收益，还应该关注风险，投资组合的风险一般以其的方差（或标准差)来衡量：

\[Var(Rp)=\sum_{i=1}^{N}{W_{i}^2}\sigma_{i}^2+\sum_{i=1}^{N}{}\sum_{j\ne1}^{N}{W_{i}W_{j}\rho_{ij}\sigma_{i}\sigma_{j}}
\]

其中：$\sigma$为$i$或$j$资产的标准差,$\rho_{ij}$为$i$资产和或$j$资产之间的相关系数。

在发达的证券市场中，马科维茨投资组合理论早已在实践中被证明是行之有效的，并且被广泛应用于组合选择和资产配置。但是，我国的证券理论界和实务界对于该理论是否适合于我国股票市场一直存有较大争议。

从狭义的角度来说，投资组合是规定了投资比例的一揽子有价证券，当然，单只证券也可以当作特殊的投资组合。本文讨论的投资组合限于由股票和无风险资产构成的投资组合。

马科维茨的投资组合理论认为，单只股票的风险由系统性风险和非系统性风险构成，投资组合可以降低非系统性风险。

1.3 资本市场线CML

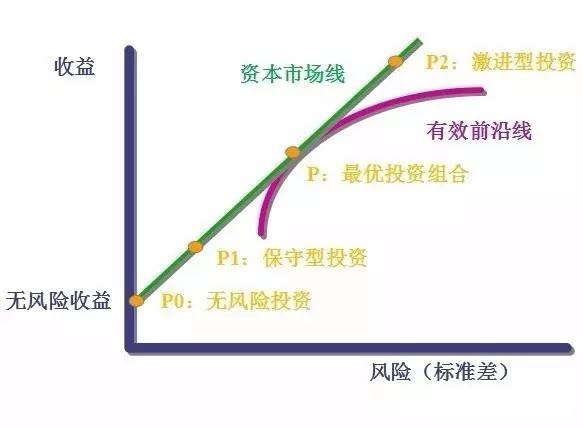
把市场上的无风险收益品种(例如国债，标准差为0)拿进来，也加入到投资组合中。任何投资品种和无风险品种组合都是一条直线。如果一条直线经过无风险收益点，并且与有效前沿线相切，那么这条直线的任何点都比有效前沿线更优。也就是说，在承担相同风险的情况下，可以获得更高的收益。如果可以以无风险利率从市场上借到钱，那么这条直线就可以延伸到切线以外，获得更高的收益。这条直线叫做资本市场线。

在下图中，P是有效前沿线与资本市场线的切点，也是最优投资组合。将最优投资组合与无风险收益品种结合起来，不同风险偏好的人，可以获得不同的收益。P1为保守型投资组合，大部分资金放在无风险收益上，小部分分配在最优投资组合上。P2为激进型投资组合，从市场借钱投资到最优投资组合上，在承担高风险的情况下获得更高的回报。

1.4 夏普比率

夏普比率（Sharpe Ratio），又被称为夏普指数——基金绩效评价标准化指标。夏普比率在现代投资理论的研究表明，风险的大小在决定组合的表现上具有基础性的作用。风险调整后的收益率就是一个可以同时对收益与风险加以考虑的综合指标，以期能够排除风险因素对绩效评估的不利影响。夏普比率就是一个可以同时对收益与风险加以综合考虑的三大经典指标之一。投资中有一个常规的特点，即投资标的的预期报酬越高，投资人所能忍受的波动风险越高；反之，预期报酬越低，波动风险也越低。所以理性的投资人选择投资标的与投资组合的主要目的为：在固定所能承受的风险下，追求最大的报酬；或在固定的预期报酬下，追求最低的风险。

\[sharperatio =\frac{E(R_p)－R_f}{\sigma_p}
\]

夏普比率= (投资组合预期报酬率 - 无风险利率 )/投资组合的标准差。$E(R_p)$：投资组合预期报酬率;$R_f$；无风险利率；$\sigma_p$：投资组合的标准差。目的是计算投资组合每承受一单位总风险，会产生多少的超额报酬。比率依据资产配置线 (Capital Allocation Line,CAL) 的观念而来，是市场上最常见的衡量比率。当投资组合内的资产皆为风险性资产时，适用夏普比率。夏普指数代表投资人每多承担一分风险，可以拿到几分超额报酬；若为正值，代表基金报酬率高过波动风险；若为负值，代表基金操作风险大过于报酬率。这样一来，每个投资组合都可以计算 Sharpe Ratio, 即投资回报与多冒风险的比例，这个比例越高，投资组合越佳。举例而言，假如国债的回报是 3%，而您的投资组合预期回报是 15%，您的投资组合的标准偏差是 6%，那么用 15%－3%, 可以得出 12%（代表您超出无风险投资的回报），再用 12%/6%=2，代表投资者风险每增长 1%，换来的是 2% 的多余收益。

夏普比率告诉我们，投资时也要比较风险，尽可能用科学的方法以冒小风险来换大回报。所以说，投资者应该成熟起来，尽量避免一些不值得冒的风险。同时当您在投资时如缺乏投资经验与研究时间，可以让真正的专业人士（不是只会卖金融产品给你的 SALER）来帮到您建立起适合自己的，可承受风险最小化的投资组合。这些投资组合可以通过夏普比率来衡量出风险和回报比例。

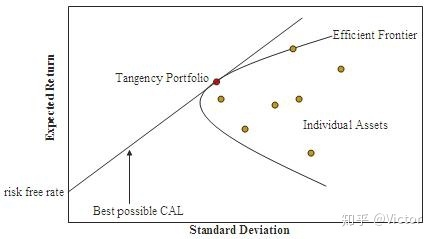
我们可以通过有效边界获取有些有效的信息帮助投资，如：Effcient Frontier向Y轴凸出的顶点是组合中风险最低的投资组合(不是红点）。资产边界上所有的点都是在相同的期望收益率情况下风险最低的投资比例组合。如果存在无风险资产（如银行理财，国债，定期（并非无风险，而是极低风险，这视为无风险）），可以投资，投资组合的可能性将被扩展（托宾模型）。存在无风险资产时存在最佳的投资组合（夏普比率理论）为红点。

综上所述，投资组合的目标就是计算这些可以帮助我们进行投资的关键点。

二、fPortfolio包

我们说到一个投资组合有四个要素需要考虑：投资模型，资产数据，投资约束条件，资产选择函数。fPortfolio包的4个主要的类（class）就是围绕这4个要素设立的。

2.1 投资模型（portfolioSpec）

一个投资模型包括投资的方法，也就是模型的类别（如：均值方差模型，均值—VAR模型，均值—下偏矩模型等）；优化的对象（前面提到的目标函数，如风险最小，收益最大等）；估计风险的方法（如马克维茨提到的利用协方差得到的β值测定风险）等诸多因素。一个组合还需要提供一些必要的信息：预期收益，预期风险，无风险利率（这个通常使用一年期的国债利率）等。这些在设定模型时十分重要，在R中设置模型时参数列表如下：

portfolioSpec(

   model = list(type = "MV", optimize = "minRisk",

   estimator = "covEstimator", tailRisk = list(),

   params = list(alpha = 0.05, a = 1)),

   portfolio = list(weights = NULL, targetReturn = NULL,

   targetRisk = NULL, riskFreeRate =0, nFrontierPoints = 50,status = NA),

   optim = list(solver = "solveRquadprog", objective = NULL,

   options = list(meq = 2), control = list(), trace = FALSE),

   messages = list())

#其中optim设置最优化的处理，暂时可以采用默认的方法。对参数的设定我们可以在建模伊始便设置好，也可以通过settype，setriskFreeRate等函数设置它们。如：

library(fPortfolio)

myspec<-portfolioSpec()

getType(myspec)

setType(myspec)<-"CVaR"

setRiskFreeRate(myspec)<-1e-8

2.2 资产数据（portfolioData）

这个是最重要的部分了，如果不能导入数据，那么我们的努力将要白费。设置数据的函数为portfolioData。参数如下：

#我们以R中的内置数据LPP2005.RET为例：

lppData<-portfolioData(data=100*LPP2005.RET,spec= portfolioSpec())

print(lppData)

注：对于每一部分的查看可以使用$，也可以使用getData,getStatistics来查看，修改用对应的set函数。这里data的类型是list，也就是这些数据要做成一个dataframe扔进函数里。

2.3 约束条件（portfolioconstraint）

对于约束我想至少是有这么几种：允许卖空，存在无风险借贷；不允许卖空，存在无风险借贷；允许卖空，不存在无风险借贷；不许卖空，也没有无风险借贷。而我们的约束条件就是要处理这些东西的。关于这几种情况，portfolioconstraints类里提供了longonly(不许卖空)，short（没有限制），还有很精细的minW[],maxW[]

对于这几个，我们还是以LPP2005为例来展示：

Data<-100*LPP2005.RET

myspec<-portfolioSpec()

constraints<-"longonly"

defaultconstrains<-portfolioConstraints(Data,myspec,constraints)

print(defaultconstrains)

b1<-"minW[1:9]=0.1"

b2<-"maxW[1:5]=0.5"

b3<-"maxW[6:9]=c(0.3,0.4,0.5,0.7)"

constraints<-c(b1,b2,b3)

defaultconstrains<-portfolioConstraints(Data,myspec,constraints)

print(defaultconstrains)

2.4 选择函数（portfolio）

主要的函数有以下几个：

efficientPortfolio(data, spec = portfolioSpec(), constraints = "LongOnly")

maxratioPortfolio(data, spec = portfolioSpec(), constraints = "LongOnly")

tangencyPortfolio(data, spec = portfolioSpec(), constraints = "LongOnly")

minriskPortfolio(data, spec = portfolioSpec(), constraints = "LongOnly")

minvariancePortfolio(data, spec = portfolioSpec(), constraints = "LongOnly")

maxreturnPortfolio(data, spec = portfolioSpec(), constraints = "LongOnly")

三、分析计算

对于A股，pedquant包是一个更好的选择。“pedquant”意指”公共经济数据和量化分析“（Public Economic Data and Quantitative Analysis）。penquant提供了对国内和国际金融数据和经济数据的访问接口，数据来源包括中国国家统计局（NBS）、FRED、雅虎财经、163财经等。同时，pedquant还提供了一些基本的图形和分析工具。R中pedquant包提供的函数主要分为三大类：

ed_ (economic data 的缩写) 开头的函数，获取来自美联储经济数据 FRED、中国人民银行 PBC (进行中)、国家统计局 NBS 等机构的经济社会统计数据；

md_ (market data 的缩写)开头的函数，获取来自雅虎财经 yahoo 的全球股票价格数据、网易财经 163 的上证与深证股票价格与财报数据、新浪财经 sina 的国内期货价格数据等；

pq_ (pedquant 的缩写)开头的函数，主要提供了一些数据预处理与可视化等相关功能。

library(pedquant)

library(openxlsx)

library(timeSeries)

library(ggplot2)

library(dplyr)

d163<-md_stock("601318.sh",from='2019-01-01',to='2022-08-01',source="163",adjust=NULL)

zgpa=data.frame(d163[[1]]$date,d163[[1]]$close)

股票收益率的数据结构见下图

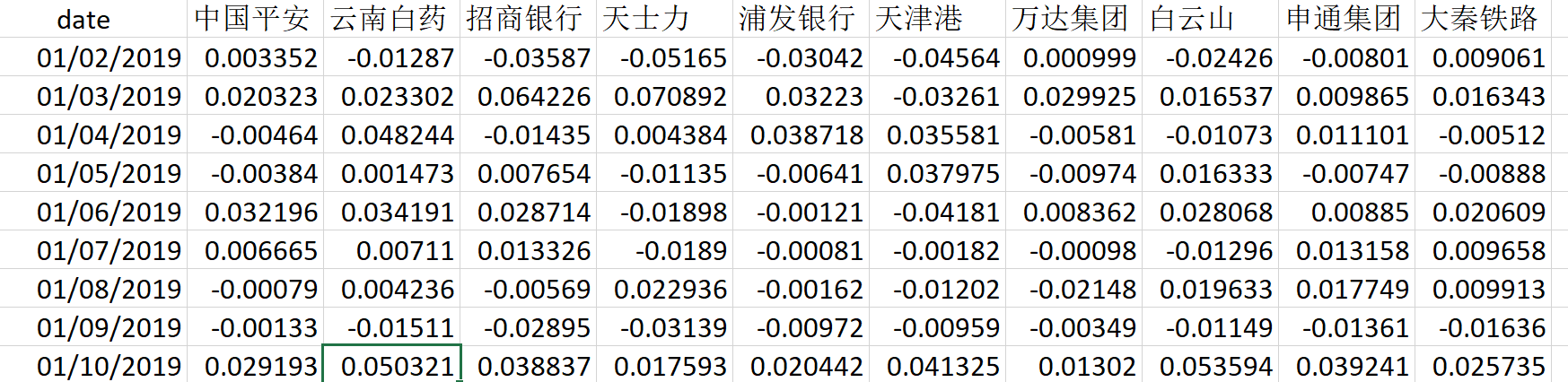
#读取股票收益率数据

data<-read.xlsx("hh10.xlsx")

data_ret<- data[,2:4]

投资组合计算可视化：

dat=as.timeSeries(data_ret)

Spec = portfolioSpec()

# Change Risk Free Rate

setRiskFreeRate(Spec) = 1e-8

Frontier = portfolioFrontier(dat,spec = Spec)

plot(Frontier)

调用 plot 函数可以对上述结果进行绘图。调用之后，R 控制台会返回一组绘图选项卡：

Make a plot selection (or 0 to exit):

1:   Plot Efficient Frontier

2:   Add Minimum Risk Portfolio

3:   Add Tangency Portfolio

4:   Add Risk/Return of Single Assets

5:   Add Equal Weights Portfolio

6:   Add Two Asset Frontiers [LongOnly Only]

7:   Add Monte Carlo Portfolios

8:   Add Sharpe Ratio [Markowitz PF Only]

选择上面选项，得到有关的投资结果：

Selection: 1

Make a plot selection (or 0 to exit):

1:   Plot Efficient Frontier

2:   Add Minimum Risk Portfolio

3:   Add Tangency Portfolio

4:   Add Risk/Return of Single Assets

5:   Add Equal Weights Portfolio

6:   Add Two Asset Frontiers [LongOnly Only]

7:   Add Monte Carlo Portfolios

8:   Add Sharpe Ratio [Markowitz PF Only]

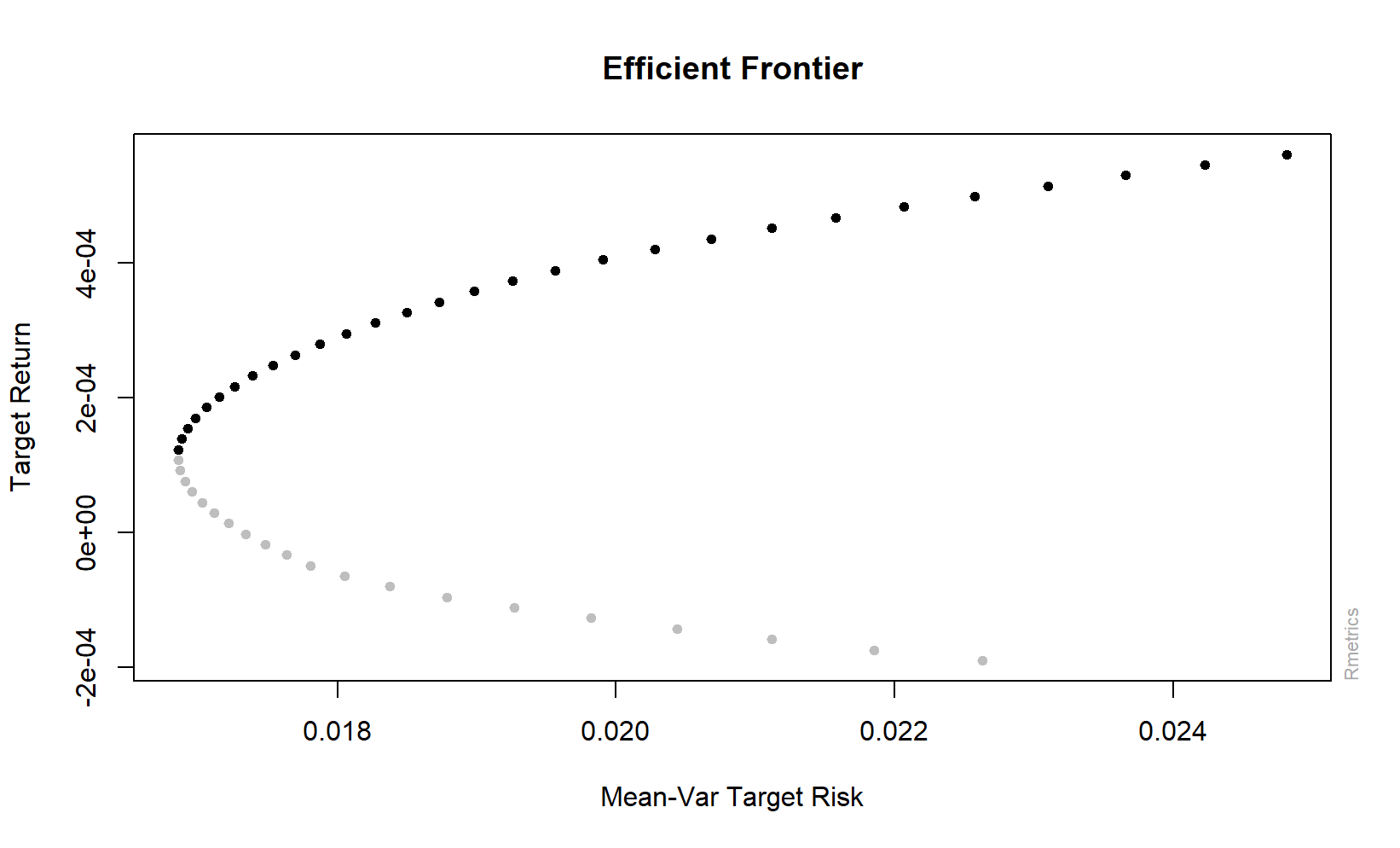
Selection: 7

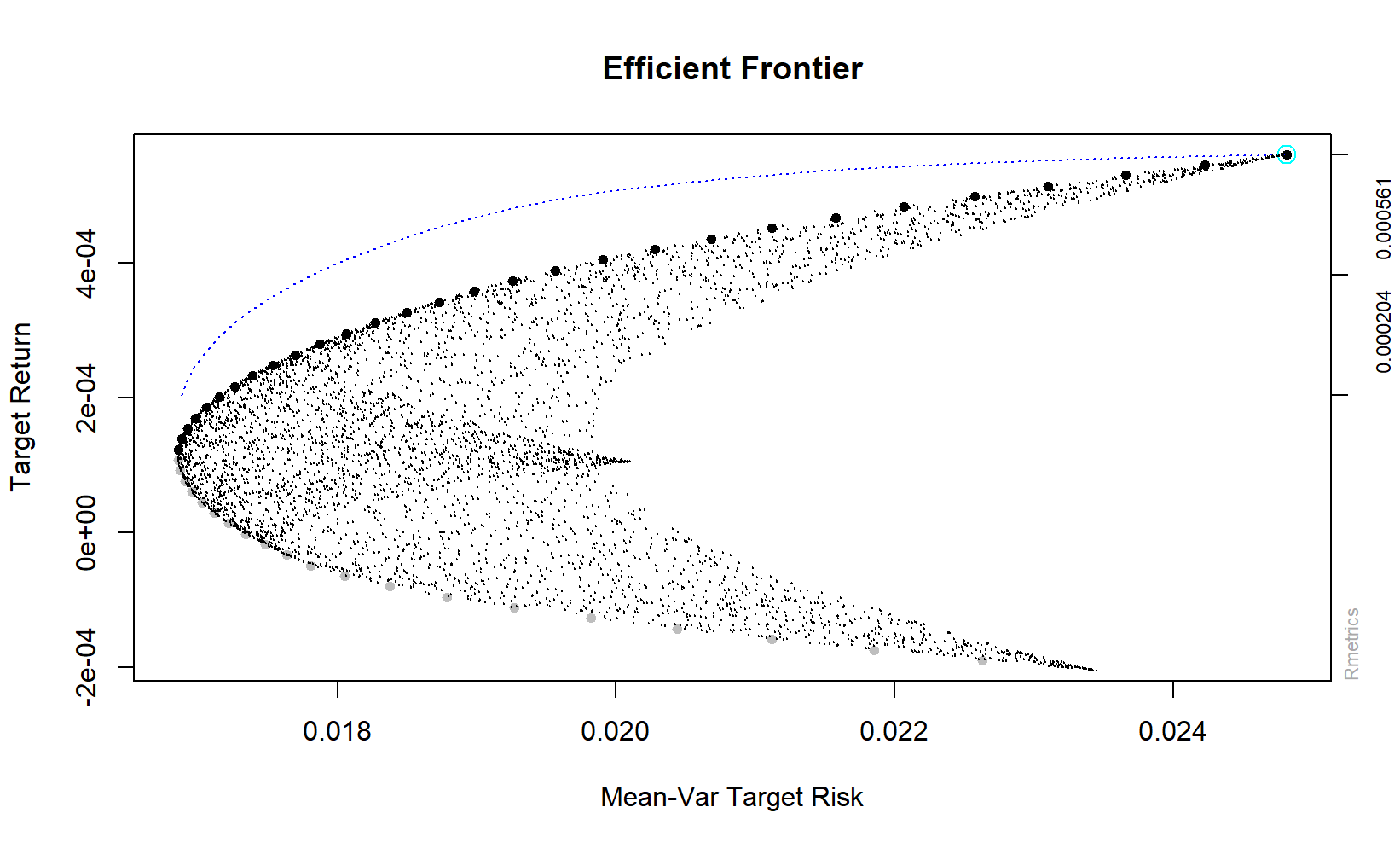
四、总结

上述内容大部分是由美国经济学家马克维茨提出的，称为现代投资组合理论，他也因此获得了诺贝尔经济学奖。夏普比率相关内容是由美国经济学家夏普等人提出的，称为资本资产定价模型。现代投资组合理论和资本资产定价模型目前已经广泛的应用到了投资决策和资产配置中。以哈佛大学捐赠基金为例，它管理着超过350亿美元的资产，2016年资产配置情况为：美国股票10.5%，其他发达国家股票7%，新兴市场股票11.5%，私募20%，对冲基金14%，房地产14.5%，自然资源10%，国内债券9%，国外债券1%，抵通胀债券2%，高收益债券0.5%。大家可能也听说过咱们国家养老金要进入股市的情况，有些人可能也会担心国家把养老金炒股给亏光。其实不用担心，养老金投资股市的比例还是比较低的，主要是起一个多元化投资的作用，最终组合后的风险比原来单一持有债券还要低。

参考文献

1.(资产组合理论选择最佳的股票投资比例 R语言量化投资)[https://zhuanlan.zhihu.com/p/139758678]

2.(R语言与马克维茨资产组合理论学习笔记（fportfolio包简介）)[https://blog.csdn.net/yujunbeta/article/details/8247799]

3.(使用R语言构造投资组合)[http://www.manongjc.com/detail/50-fjbibjbaapshmaq.html]