RNN神经网络产生梯度消失和梯度爆炸的原因及解决方案

1、RNN模型结构

　　循环神经网络RNN（Recurrent Neural Network）会记忆之前的信息，并利用之前的信息影响后面结点的输出。也就是说，循环神经网络的隐藏层之间的结点是有连接的，隐藏层的输入不仅包括输入层的输出，还包括上时刻隐藏层的输出。下图为RNN模型结构图：

2、RNN前向传播算法

RNN前向传播公式为：

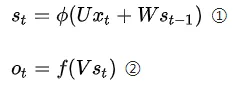
　　其中：

　　　　S_t为t时刻的隐含层状态值；

　　　　O_t为t时刻的输出值；

　　　　①是隐含层计算公式，U是输入x的权重矩阵，S_t-1是t-1时刻的状态值，W是S_t-1作为输入的权重矩阵，$\Phi $是激活函数；

　　　　②是输出层计算公司，V是输出层的权重矩阵，f是激活函数。

　　损失函数（loss function）采用交叉熵$L_{t}=-\overline{o_{t}}logo_{_{t}}$（O_t是t时刻预测输出，$\overline{o_{t}}$是t时刻正确的输出）

那么对于一次训练任务中，损失函数$L=\sum_{i=1}^{T}-\overline{o_{t}}logo_{_{t}}$， T是序列总长度。

假设初始状态S_t为0，t=3 有三段时间序列时，由 ① 带入②可得到

　　t1、t2、t3 各个状态和输出为：

　　t=1：

　　　　状态值：$s_{1}=\Phi (Ux_{1}+Ws_{0})$

　　　　输出：$o_{1}=f(V\Phi (Ux_{1}+Ws_{0}))$

　　t=2：

　　　　状态值：$s_{2}=\Phi (Ux_{2}+Ws_{1})$

　　　　输出：$o_{2}=f(V\Phi (Ux_{2}+Ws_{1}))=f(V\Phi (Ux_{2}+W\Phi(Ux_{1}+Ws_{0})))$

　　t=3：

　　　　状态值：$s_{3}=\Phi (Ux_{3}+Ws_{2})$

　　　　输出：$o_{3}=f(V\Phi (Ux_{3}+Ws_{2}))=\cdots =f(V\Phi (Ux_{3}+W\Phi(Ux_{2}+W\Phi(Ux_{1}+Ws_{0}))))$

3、RNN反向传播算法

　　BPTT（back-propagation through time）算法是针对循层的训练算法，它的基本原理和BP算法一样。其算法本质还是梯度下降法，那么该算法的关键就是计算各个参数的梯度，对于RNN来说参数有 U、W、V。

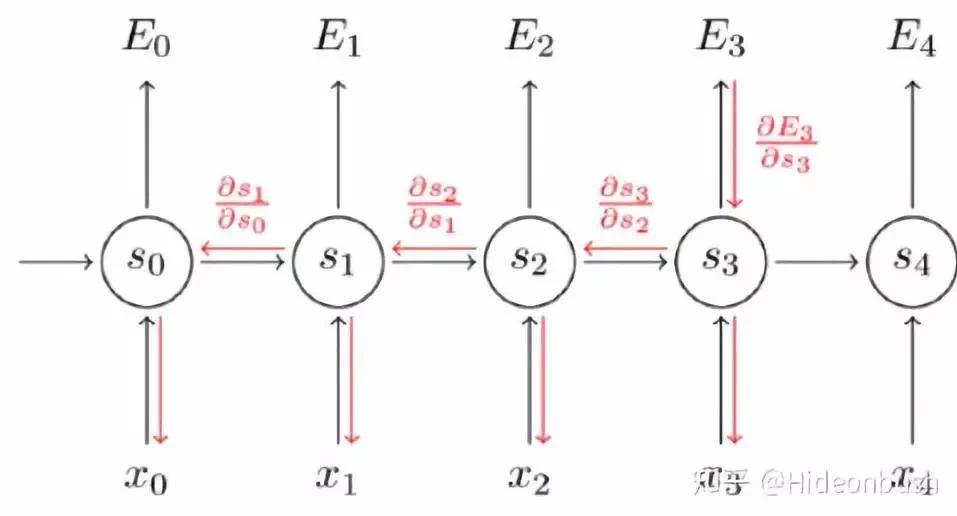
反向传播

　　现对t=3时刻的U、W、V求偏导，由链式法则得到：

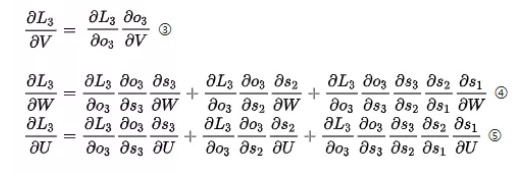
可以简写成：

　　观察③④⑤式，可知，对于 V 求偏导不存在依赖问题；但是对于 W、U 求偏导的时候，由于时间序列长度，存在长期依赖的情况。主要原因可由 t=1、2、3 的情况观察得 , S_t会随着时间序列向前传播，同时S_t是 U、W 的函数。

　　前面得出的求偏导公式⑥，取其中累乘的部分出来，其中激活函数 Φ 通常是tanh函数 ，则

4、梯度爆炸和梯度消失的原因

　　激活函数tanh和它的导数图像如下:

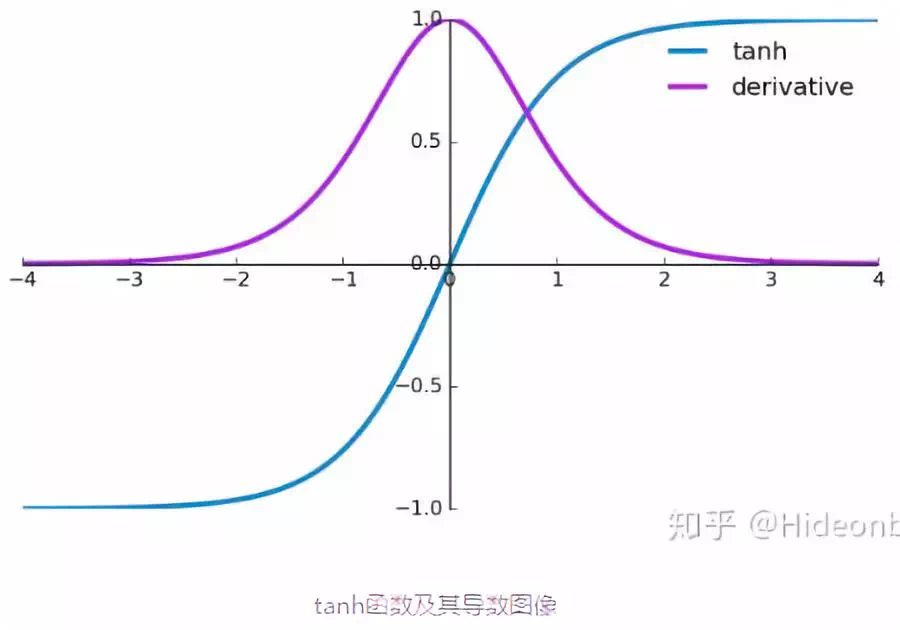
由上图可知当激活函数是tanh函数时，tanh函数的导数最大值为1，又不可能一直都取1这种情况，实际上这种情况很少出现，那么也就是说，大部分都是小于1的数在做累乘，若当t很大的时候，$\prod_{j=k-1}^{t}tan{h}'W$中的$\prod_{j=k-1}^{t}tan{h}'$趋向0，举个例子：0.8⁵⁰=0.00001427247也已经接近0了，这是RNN中梯度消失的原因。

再看⑦部分：

$\prod_{j=k-1}^{3}\frac{\partial s_{j}}{\partial s_{j-1}}=\prod_{j=k-1}^{3}tan{h}'W$

如果参数 W 中的值太大，随着序列长度同样存在长期依赖的情况，$\prod_{j=k-1}^{t}tan{h}'W$中的$\prod_{j=k-1}^{t}tan{h}'$趋向于无穷，那么产生问题就是梯度爆炸。

在平时运用中，RNN比较深，使得梯度爆炸或者梯度消失问题会比较明显。

5、解决梯度爆炸和梯度消失的方案

1）采使用ReLu激活函数

　　面对梯度消失问题，可以采用ReLu作为激活函数，下图为ReLu函数：

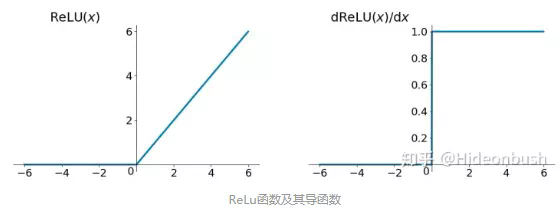
　　ReLU函数在定义域大于0部分的导数恒等于1，这样可以解决梯度消失的问题，（虽然恒等于1很容易发生梯度爆炸的情况，但可通过设置适当的阈值可解决）。

另外计算方便，计算速度快，可以加速网络训练。但是，定义域负数部分恒等于零，这样会造成神经元无法激活（可通过合理设置学习率，降低发生的概率）。

　　ReLU有优点也有缺点，其中的缺点可以通过其他操作取避免或者减低发生的概率，是目前使用最多的激活函数。

还可以通过更改内部结构来解决梯度消失和梯度爆炸问题，那就是LSTM了。

2）使用长短记忆网络LSTM

　　使用长短期记忆（LSTM）单元和相关的门类型神经元结构可以减少梯度爆炸和梯度消失问题，LSTM的经典图为：

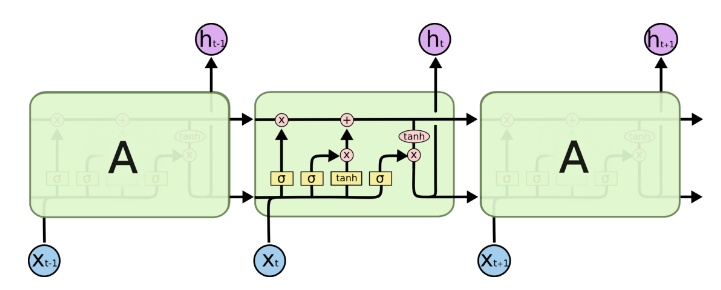
可以抽象为：

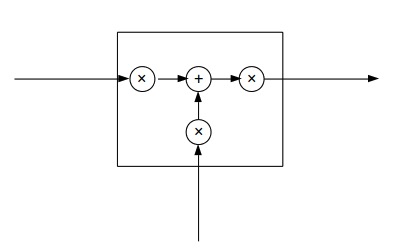
　　三个×分别代表的就是forget gate，input gate，output gate，而我认为LSTM最关键的就是forget gate这个部件。这三个gate是如何控制流入流出的呢，其实就是通过下面 _ft，it，ot 三个函数来控制，因为$\sigma (x)$代表sigmoid函数） 的值是介于0到1之间的，刚好用趋近于0时表示流入不能通过gate，趋近于1时表示流入可以通过gate。

$f_{t}=\sigma (W_{f}X_{t}+b_{f})$

$i_{t}=\sigma (W_{i}X_{t}+b_{i)$

$o_{t}=\sigma (W_{o}X_{t}+b_{o})$

　　LSTM当前的状态值为： $S_{t}=f_{t}S_{t-1}+i_{t}X_{t}$，表达式展开后得：

$S_{t}=\sigma (W_{f}X_{t}+b_{f})S_{t-1}+\sigma (W_{i}X_{t}+b_{i})X_{t}$

　　如果加上激活函数:

$S_{t}=tanh[\sigma (W_{f}X_{t}+b_{f})S_{t-1}+\sigma (W_{i}X_{t}+b_{i})X_{t}]$

　　上文中讲到传统RNN求偏导的过程包含：

$\prod_{j=k-1}^{t}\frac{\partial s_{j}}{\partial s_{j-1}}=\prod_{j=k-1}^{t}tan{h}'W$

　　对于LSTM同样也包含这样的一项，但是在LSTM中 为：

$\prod_{j=k-1}^{t}\frac{\partial s_{j}}{\partial s_{j-1}}=\prod_{j=k-1}^{t}tan{h}'(W_{f}X_{t}+b_{f})$

　　假设$Z=tanh'(x)\sigma (y)$，则Z的函数图像如下图所示：

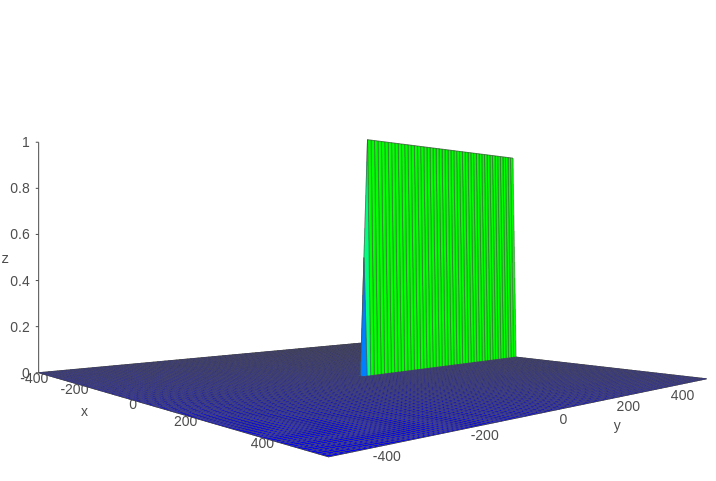
　　可以看到该函数值基本上不是0就是1。

　　传统RNN的求偏导过程：

$\frac{\sigma L_{3}}{\sigma W}=\sum_{k=0}^{t}\frac{\partial L_{3}}{\partial o_{3}}\frac{\partial o_{3}}{\partial s_{3}}(\prod_{j=k-1}^{3}\frac{\partial s_{j}}{\partial s_{j-1}})\frac{\partial s_{k}}{\partial W}$

　　如果在LSTM中上式可能就会变成：

$\frac{\sigma L_{3}}{\sigma W}=\sum_{k=0}^{t}\frac{\partial L_{3}}{\partial o_{3}}\frac{\partial o_{3}}{\partial s_{3}}\frac{\partial s_{k}}{\partial W}$

　　因为$\prod_{j=k-1}^{3}\frac{\partial s_{j}}{\partial s_{j-1}}=\prod_{j=k-1}^{3}tan{h}'\sigma (W_{f}X_{t}+b_{f})\approx 0|1$，这样解决了传统RNN中梯度消失的问题。

参考

　　https://www.jiqizhixin.com/articles/2019-01-17-7

　　https://zhuanlan.zhihu.com/p/28687529