[Luogu P1119] 灾后重建 (floyd)

题面

传送门:https://www.luogu.org/problemnew/show/P1119

---

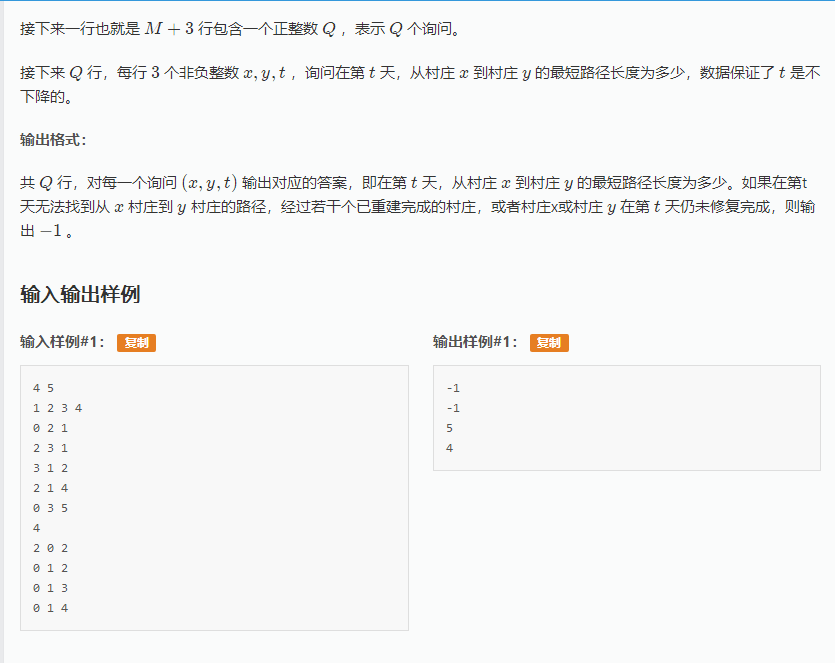
Solution

这题的思想很巧妙.

首先,我们可以考虑一下最暴力的做法,对每个时刻的所有点都求一遍单元最短路

因为最多只有200个时刻,时间复杂度为O(n^3log(n+m))) (堆优化的迪杰斯特拉)

显然对于n=200,并过不了

我们可有进一步分析

这一题,我们堆优化的迪杰斯特拉慢在每加入一个点,我们每一次都得对全图彻彻底底做一轮松弛

那换个角度考虑,如果我只松弛经过新加入的点的点对呢?

没错,就得用Floyd了.

因为Floyd本质就是一个DP,给了我们极大的魔改的空间

考虑到Floyd最外层循环就是枚举加入的点,我们就可以只枚举里面那两层枚举点对的循环.

也就是说我们只用考虑它有可能松弛到的点.

当然,在此之前,我们得先把这个点有关的边先连回去

然后先用两层循环(枚举中转点和起始点)来松弛终点为加入点的路径

接下来用刚刚说的两层循环来松弛经过新加入点路径就好

时间复杂度O(n^3)

然后就OjbK了

具体请看代码

---

Code

//Luogu P1119 灾后重建
//May,28th,2018
//巧妙的floyed松弛
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=200+10;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
int n,m,T[N],dis[N][N],e[N][N];
int main()
{
    n=read(),m=read();
    memset(T,0x3f,sizeof T);
    memset(dis,0x3f,sizeof dis);
    memset(e,0x3f,sizeof e);
    for(int i=0;i<n;i++)
        T[i]=read();
    for(int i=1;i<=m;i++)
    {
        int a=read(),b=read(),temp=read();
        e[a][b]=e[b][a]=temp;
    }
 
    for(int i=0;i<n;i++)
        e[i][i]=dis[i][i]=0;
    int Q=read(),to=0;
    for(int i=1;i<=Q;i++)
    {
        int x=read(),y=read(),t=read();
        while(T[to]<=t)
        {
            for(int j=0;T[j]<=t;j++)
                dis[to][j]=dis[j][to]=min(dis[to][j],e[to][j]);
            for(int j=0;T[j]<=t;j++)
                for(int k=0;T[k]<=t;k++)
                    dis[to][k]=dis[k][to]=min(dis[k][to],dis[k][j]+dis[j][to]);
            for(int j=0;T[j]<=t;j++)
                for(int k=0;T[k]<=t;k++)
                    dis[j][k]=min(dis[j][k],dis[j][to]+dis[to][k]);
            to++;
        }
        if(dis[x][y]==0x3f3f3f3f)
            printf("-1\n");
        else
            printf("%d\n",dis[x][y]);
    }
    return 0;
}

正解(c++)