Java 内功修炼 之 数据结构与算法（二）
一、二叉树补充、多叉树
1、二叉树（非递归实现遍历）
（1）前提
前面一篇介绍了 二叉树、顺序二叉树、线索二叉树、哈夫曼树等树结构。
可参考：https://www.cnblogs.com/l-y-h/p/13751459.html#_label5_1
（2）二叉树遍历
【递归与非递归实现：】
使用递归实现时，系统隐式的维护了一个栈 用于操作节点。虽然递归代码易理解，但是对于系统的性能会造成一定的影响。
使用非递归代码实现，可以主动去维护一个栈 用于操作节点。非递归代码相对于递归代码，其性能可能会稍好（数据大的情况下）。
注：
栈是先进后出（后进先出）结构，即先存放的节点后输出（后存放的节点先输出）。
所以使用栈时，需要明确每一步需要压入的树节点。
递归实现二叉树 前序、中序、后序遍历。可参考：https://www.cnblogs.com/l-y-h/p/13751459.html#_label5_2
（3）非递归实现前序遍历
【非递归实现前序遍历：】
前序遍历顺序：当前节点（父节点）、左子节点、右子节点。
实现思路：
首先明确一点，每次出栈的树节点即为当前需要输出的节点（第一个输出的节点为 根节点）。 每次首先输出的为 当前节点（父节点），所以父节点先入栈、再出栈。
出栈之后，需要重新选择出下一次需要输出的父节点。从当前节点的 左、右子节点中选择。
而左子节点需要在 右子节点前输出，所以右子节点需要先进栈，然后左子节点再进栈。
左子节点入栈后，再次出栈即为当前节点，然后重复上面操作，依次取出栈顶元素即可。 步骤：
Step1：根节点入栈。
Step2：根节点出栈，此时为当前节点，输出或者保存。
Step2.1：若当前节点存在右子节点，则压入栈。
Step2.2：若当前节点存在左子节点，则压入栈。
Step3：重复 Step2，依次取出栈顶元素并输出，栈为空时，则树遍历完成。 【非递归前序遍历代码实现：】
package com.lyh.tree; import java.util.ArrayList;
import java.util.List;
import java.util.Stack; public class BinaryTreeSort<K> {
/**
* 前序遍历（非递归实现、使用栈模拟递归）
*/
public List<K> prefixList(TreeNode9<K> root) {
// 使用集合保存最终结果
List<K> result = new ArrayList<>();
// 根节点不存在时，返回空集合
if (root == null) {
return result;
}
// 使用栈模拟递归
Stack<TreeNode9<K>> stack = new Stack<>();
// 根节点入栈
stack.push(root);
// 栈非空时，依次取出栈顶元素，此时栈顶元素为当前节点，输出，并将当前节点 左、右子节点入栈
// 左子节点 先于 右子节点出栈，所以左子节点在 右子节点入栈之后再入栈
while(!stack.isEmpty()) {
// 取出栈顶元素（当前节点）
TreeNode9<K> tempNode = stack.pop();
// 保存（或者输出）当前节点
result.add(tempNode.data);
// 存在右子节点，则压入栈
if (tempNode.right != null) {
stack.push(tempNode.right);
}
// 存在左子节点，则压入栈
if (tempNode.left != null) {
stack.push(tempNode.left);
}
}
return result;
} public static void main(String[] args) {
// 构建二叉树
TreeNode9<String> root = new TreeNode9<>("0");
TreeNode9<String> treeNode = new TreeNode9<>("1");
TreeNode9<String> treeNode2 = new TreeNode9<>("2");
TreeNode9<String> treeNode3 = new TreeNode9<>("3");
TreeNode9<String> treeNode4 = new TreeNode9<>("4");
root.left = treeNode;
root.right = treeNode2;
treeNode.left = treeNode3;
treeNode.right = treeNode4; // 前序遍历
System.out.print("前序遍历： ");
System.out.println(new BinaryTreeSort<String>().prefixList(root));
System.out.println("\n=====================");
} } class TreeNode9<K> {
K data; // 保存节点数据
TreeNode9<K> left; // 保存节点的 左子节点
TreeNode9<K> right; // 保存节点的 右子节点 public TreeNode9(K data) {
this.data = data;
} @Override
public String toString() {
return "TreeNode9{ data= " + data + "}";
}
} 【输出结果：】
前序遍历： [0, 1, 3, 4, 2]
（4）非递归实现中序遍历
【非递归实现中序遍历：】
中序遍历顺序：左子节点、当前节点、右子节点。
实现思路：
首先明确一点，每次出栈的树节点即为当前需要输出的节点（第一次输出的节点为 最左侧节点）。 由于每次都要先输出当前节点的最左侧节点，所以需要遍历找到这个节点。
而在遍历的过程中，每次经过的树节点均为 父节点，可以使用栈保存起来。
此时，找到并输出最左侧节点后，就可以出栈获得父节点，然后根据父节点可以找到其右子节点。
将右子节点入栈，同理找到其最左子节点，并重复上面操作，依次取出栈顶元素即可。
注：
为了防止重复执行父节点遍历左子节点的操作，可以使用辅助变量记录当前操作的节点。 步骤：
Step1：记当前节点为根节点，从根节点开始，遍历找到最左子节点，并依次将经过的树节点入栈。
Step2：取出栈顶元素，此时为最左子节点（当前节点），输出或者保存。
Step2.1：若存在右子节点，则当前节点为 父节点，将右子节点入栈，并修改新的当前节点为 右子节点。遍历当前节点，同理找到最左子节点，并依次将经过的节点入栈。
Step2.2：若不存在右子节点，则当前节点为 左子节点，下一次取得的栈顶元素即为 父节点。
Step3：重复上面过程，输出顺序即为 左、根、右。 【非递归中序遍历代码实现：】
package com.lyh.tree; import java.util.ArrayList;
import java.util.List;
import java.util.Stack; public class BinaryTreeSort<K> { /**
* 中序遍历（非递归实现，使用栈模拟递归）
*/
public List<K> infixList(TreeNode9<K> root) {
// 使用集合保存遍历结果
List<K> result = new ArrayList<>();
if (root == null) {
return result;
}
// 保存当前节点
TreeNode9<K> currentNode = root;
// 使用栈模拟递归实现
Stack<TreeNode9<K>> stack = new Stack<>();
while(!stack.isEmpty() || currentNode != null) {
// 找到当前节点的左子节点，并依次将经过的节点入栈
while(currentNode != null) {
stack.push(currentNode);
currentNode = currentNode.left;
}
// 取出栈顶元素
TreeNode9<K> tempNode = stack.pop();
// 保存栈顶元素
result.add(tempNode.data);
// 存在右子节点，则右子节点入栈，
if (tempNode.right != null) {
currentNode = tempNode.right;
}
}
return result;
} public static void main(String[] args) {
// 构建二叉树
TreeNode9<String> root = new TreeNode9<>("0");
TreeNode9<String> treeNode = new TreeNode9<>("1");
TreeNode9<String> treeNode2 = new TreeNode9<>("2");
TreeNode9<String> treeNode3 = new TreeNode9<>("3");
TreeNode9<String> treeNode4 = new TreeNode9<>("4");
root.left = treeNode;
root.right = treeNode2;
treeNode.left = treeNode3;
treeNode.right = treeNode4; // 前序遍历
System.out.print("中序遍历： ");
System.out.println(new BinaryTreeSort<String>().infixList(root));
System.out.println("\n=====================");
} } class TreeNode9<K> {
K data; // 保存节点数据
TreeNode9<K> left; // 保存节点的 左子节点
TreeNode9<K> right; // 保存节点的 右子节点 public TreeNode9(K data) {
this.data = data;
} @Override
public String toString() {
return "TreeNode9{ data= " + data + "}";
}
} 【输出结果：】
中序遍历： [3, 1, 4, 0, 2]
（5）非递归实现后序遍历
【非递归实现后序遍历：】
后序遍历顺序：左子节点、右子节点、当前节点。
实现思路：
首先明确一点，每次出栈的树节点即为当前需要输出的节点（第一次输出的节点为最左侧节点）。 这里与 中序遍历还是有点类似的，同样是先输出最左侧节点。区别在于，后序遍历先输出 右子节点，再输出父节点。
同样使用一个变量，用来辅助遍历，防止父节点重复遍历子节点。
此处的变量，可以理解成上一次节点所在位置。而栈顶取出的当前节点为上一次节点的父节点。 步骤：
Step1：根节点入栈。
Step2：取出栈顶元素（当前节点），判断其是否存在子节点。
Step2.1：存在左子节点，且未被访问过，左子节点入栈（此处为遍历找到最左子节点）。
Step2.2：存在右子节点，且未被访问过，右子节点入栈。
Step2.3：不存在 或者 已经访问过 左、右子节点，输出当前节点。
Step3：重复以上操作，直至栈空。 【非递归后序遍历代码实现：】
package com.lyh.tree; import java.util.ArrayList;
import java.util.List;
import java.util.Stack; public class BinaryTreeSort<K> { /**
* 后序遍历（非递归实现，使用栈模拟递归）
*/
public List<K> suffixList(TreeNode9<K> root) {
// 使用集合保存遍历结果
List<K> result = new ArrayList<>();
if (root == null) {
return result;
} // 保存当前节点
TreeNode9<K> currentNode = root;
// 使用栈模拟递归实现
Stack<TreeNode9<K>> stack = new Stack<>();
// 根节点入栈
stack.push(root);
// 依次取出栈顶元素
while(!stack.isEmpty()) {
// 取出栈顶元素
TreeNode9<K> tempNode = stack.peek();
// 若当前节点 左子节点 存在，且未被访问，则入栈
if (tempNode.left != null && currentNode != tempNode.left && currentNode != tempNode.right) {
stack.push(tempNode.left);
} else if (tempNode.right != null && currentNode != tempNode.right){
// 若当前节点 右子节点存在，且未被访问，则入栈
stack.push(tempNode.right);
} else {
// 当前节点不存在 左、右子节点 或者 左、右子节点已被访问，则取出栈顶元素，
// 并标注当前节点位置，表示当前节点已被访问
result.add(stack.pop().data);
currentNode = tempNode;
}
}
return result;
} public static void main(String[] args) {
// 构建二叉树
TreeNode9<String> root = new TreeNode9<>("0");
TreeNode9<String> treeNode = new TreeNode9<>("1");
TreeNode9<String> treeNode2 = new TreeNode9<>("2");
TreeNode9<String> treeNode3 = new TreeNode9<>("3");
TreeNode9<String> treeNode4 = new TreeNode9<>("4");
root.left = treeNode;
root.right = treeNode2;
treeNode.left = treeNode3;
treeNode.right = treeNode4; // 前序遍历
System.out.print("后序遍历： ");
System.out.println(new BinaryTreeSort<String>().suffixList(root));
System.out.println("\n=====================");
} } class TreeNode9<K> {
K data; // 保存节点数据
TreeNode9<K> left; // 保存节点的 左子节点
TreeNode9<K> right; // 保存节点的 右子节点 public TreeNode9(K data) {
this.data = data;
} @Override
public String toString() {
return "TreeNode9{ data= " + data + "}";
}
} 【输出结果：】
后序遍历： [3, 4, 1, 2, 0]
2、多叉树、B树
（1）平衡二叉树可能存在的问题
平衡二叉树虽然效率高，但是当数据量非常大时（数据存放在 数据库 或者 文件中，需要经过磁盘 I/O 操作），此时构建平衡二叉树会消耗大量时间，影响程序执行速度。同时会出现大量的树节点，导致平衡二叉树的高度非常大，此时再去进行查找操作 性能也不是很高。
平衡二叉树中，每个节点有 一个数据项，以及两个子节点，那么能否增加 节点的子节点数 以及 数据项 来提高程序性能呢？从而引出了 多路查找树 的概念。
注：
前面介绍了平衡二叉树，可参考：https://www.cnblogs.com/l-y-h/p/13751459.html#_label5_9
即平衡二叉树只允许每个节点最多出现两个分支，而此处的多路查找树指的是允许出现多个分支（且分支有序）。
（2）多叉树、多路查找树
多叉树 允许每个节点 可以有 两个以上的子节点以及数据项。
多路查找树 即 平衡的多叉树（数据有序）。
常见多路查找树 有：2-3 树、B 树（B-树）、B+树、2-3-4 树 等。
（3）B 树（B-树）
B 树 即 Balanced-tree，简称 B-tree（B 树、B-树是同一个东西），是一种平衡的多路查找树。
树节点的子节点最多的数目称为树的阶。比如：2-3 树的阶为 3。2-3-4 树的阶为 4。
【一颗 M 阶的 B 树特点：（M 阶指的是最大节点的子节点个数）】
每个节点最多有 M 个子节点（子树）。
根节点存在 0 个或者 2 个以上子节点。
非叶子节点 若存在 j 个子节点，那么该非叶子节点保存 j - 1 个数据项，且按照递增顺序存储。
所有的叶子节点均在同一层。
注：
B 树是一个平衡多路查找树，具有与 平衡二叉树 类似的特点，
区别在于 B 树分支更多，从而构建出的树高度低。
当然 B 树也不能无限制的增大 树的阶，阶约大，则非叶子节点保存的数据项越多（变成了一个有序数组，增加查找时间）。
（4）2-3 树
2-3 树是最简单的 B 树，是一颗平衡多路查找树。
其节点可以分为 2 节点、3 节点，且 所有叶子节点均在同一个层。
【2-3 树特点：】
对于 2 节点：
只能包含一个数据项 和 两个子节点（或者没有子节点）。
左子节点值 小于 当前节点值，右子节点值 大于 当前节点值。
不存在只有一个子节点的情况。 对于 3 节点：
包含一大一小两个数据项（从小到大排序） 和 三个子节点（或者没有子节点）。
左子节点值 小于 当前节点数据项最小值，右子节点值 大于 当前节点数据项最大值，中子节点值 在 当前节点数据项值之间。
不存在有 1 子节点、2 个子节点的情况。
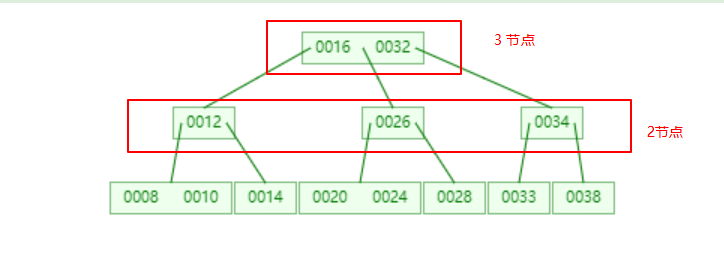
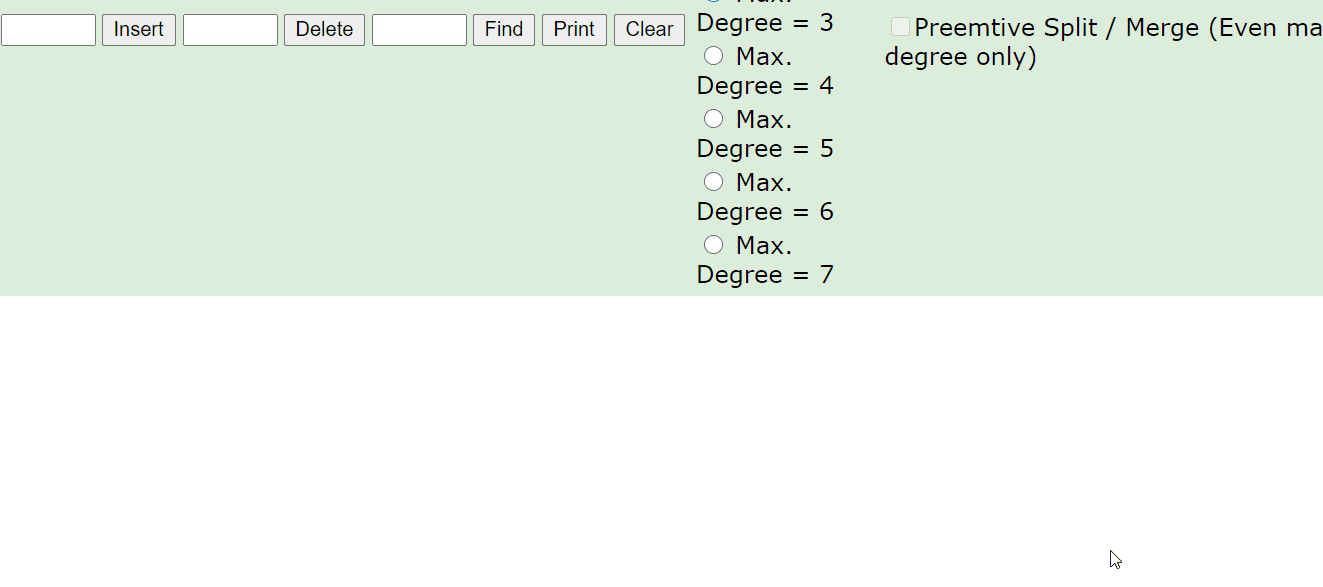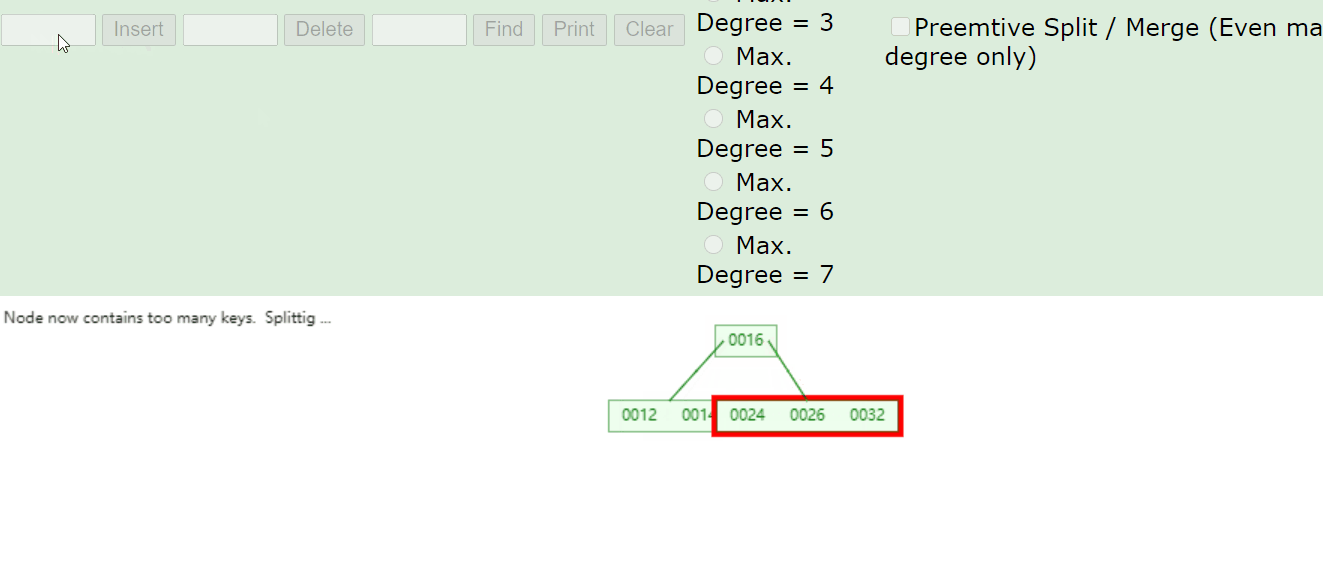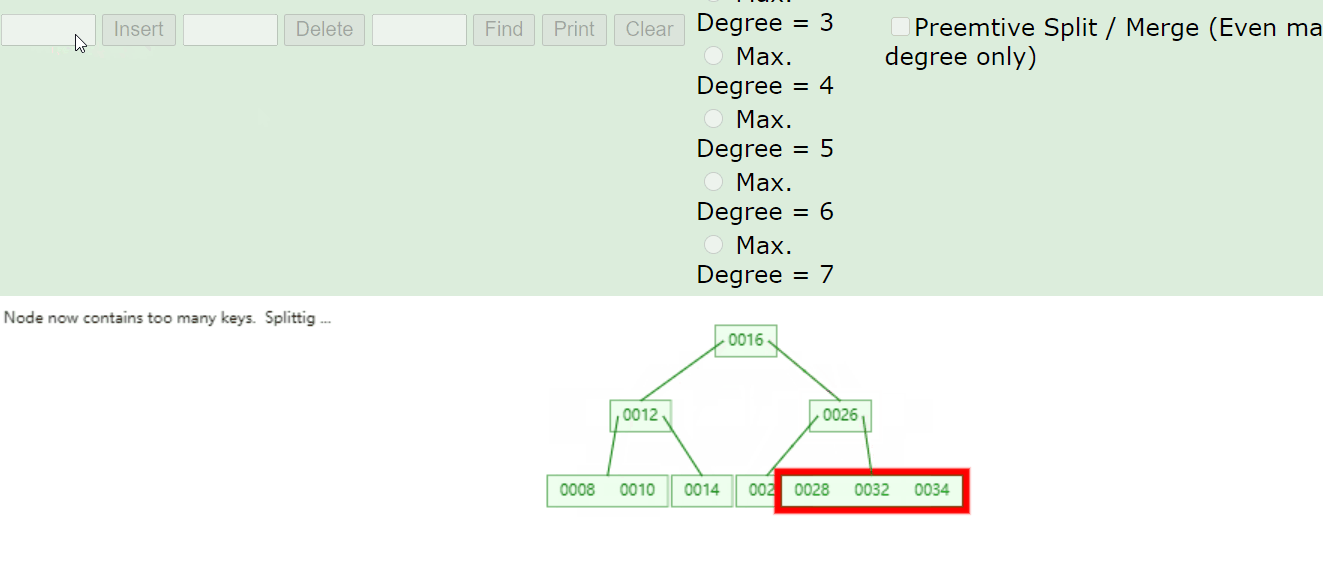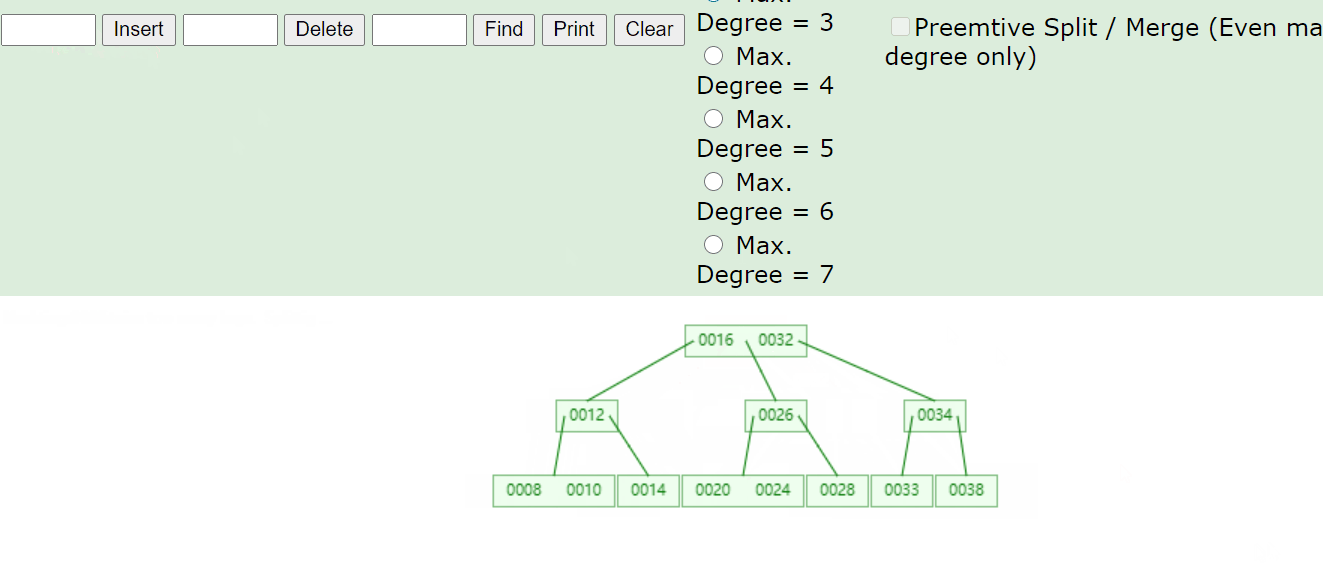
根据 {16, 24, 12, 32, 14, 26, 34, 10, 8, 28, 38, 20, 33} 构建的 2-3 树如下：
可使用 https://www.cs.usfca.edu/~galles/visualization/Algorithms.html 构建。
（5）B+ 树
B+ 树是 B 树的变种。
区别在于 B+ 树数据存储在叶子节点，数据最终只能在 叶子节点 中找到，而 B 树可以在 非叶子节点 找到。
B+ 树性能可以等价于 对 全部叶子节点（所有关键字）进行一次 二分查找。
【B+ 树特点：】
所有 数据项（关键字） 均存放于 叶子节点。
每个叶子节点 存放的 数据项（关键字）是有序的。
所有叶子节点使用链表相连（即进行范围查询时，只需要查找到 首尾节点、然后遍历链表 即可）。
注：
所有数据项（关键字） 均存放与 叶子节点组成的链表中，且数据有序，可以视为稠密索引。
非叶子节点 相当于 叶子节点的索引，可以视为 稀疏索引。
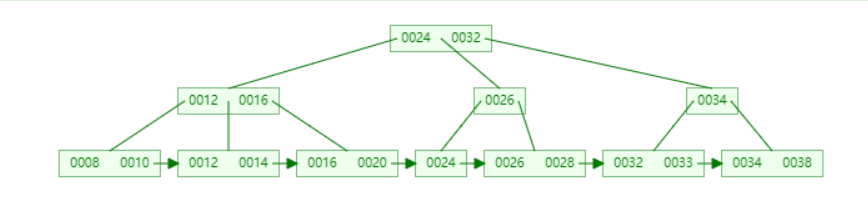
根据 {16, 24, 12, 32, 14, 26, 34, 10, 8, 28, 38, 20, 33} 构建的 B+ 树（3阶、2-3 树）如下：
（6）B* 树
B* 树 是 B+ 树的变体。
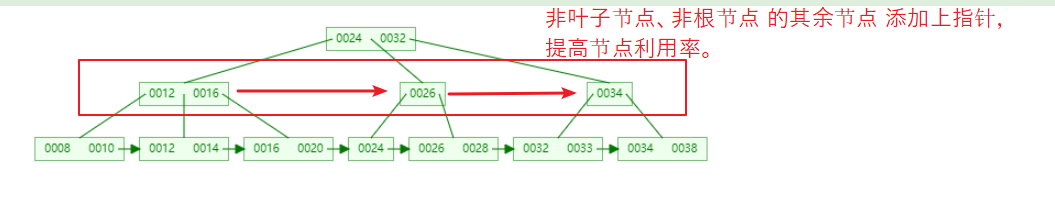
其在 B+树 基础上，在除 非根节点、非叶子节点 之外的其余节点之间增加指针，提高节点利用率。
【B* 树与 B+ 树 节点分裂的区别：】
对于 B+ 树：
B+ 树 节点的最低使用率是 1/2，其非叶子节点关键字（数据项）个数至少为 (1/2)*M。M 为 B+ 树的阶。
当一个节点存放满时，会增加一个节点，并将原节点 1/2 的数据移动到新的节点，然后在 父节点 添加新的节点。
B+ 树 只影响 原节点 以及 父节点，不会影响兄弟节点，兄弟之间不需要指针。 对于 B* 树：
B* 树 节点的最低使用率为 2/3，其非叶子节点关键字（数据项）个数至少为 (2/3)*M。
当一个节点存放满时，若其下一个兄弟节点未满，则将一部分数据移到兄弟节点中，在原节点 添加新节点，然后修改 父节点 中的节点（兄弟节点发生改变）。
若其下一个兄弟已满，则在 两个兄弟之间 增加一个新节点，并分别从两个兄弟节点中 移动 1/3 的数据到新节点，然后在 父节点 添加新的节点。
B* 树 影响了 兄弟节点，所以需要指针将兄弟节点连接起来。 总的来说，B* 树分配新节点的概率比 B+ 树低，B* 树的节点利用率更高。 注：
相关内容参考：https://blog.csdn.net/wyqwilliam/article/details/82935922
下图不一定正确，大概理解意思就行。
（7）B-树、B+树、B*树总结
【B 树 或者 B- 树：】
平衡的多路查找树，非叶子节点至少存储 (1/2)*M 个关键字（数据项），
关键字升序存储，且仅出现一次，
进行查找匹配操作时，可以在 非叶子节点 成功匹配。 【B+ 树：】
B 树的变种，仅在 叶子节点 保存数据项，且叶子节点之间 通过链表存储。
整体 数据项 有序存储。
非叶子节点 作为 叶子节点 的索引存在，匹配时通过 非叶子节点 快速定位到 叶子节点，然后在 叶子节点 处进行匹配操作，相当于进行 二分查找。 【B* 树：】
B+ 树的变种，给 非叶子节点 也加上指针，非叶子节点 至少存储 (2/3)*M 个关键字。
将节点利用率 从 1/2 提高到 2/3 。
二、延伸一下 MySQL 索引底层数据结构
1、索引（Index）
（1）索引是什么？
索引是一种有序的、快速查找的数据结构。
索引 由 若干个 索引项组成，每个索引项 由 数据的关键字 以及 其相对应的记录（比如：记录对应在磁盘中的 地址信息）组成。
索引的查找，就是根据 索引项中的关键字 去关联 其相应的记录 的过程。
（2）数据库为什么使用索引?
为了提高数据查询效率，数据库在维护数据的同时维护一个满足特定查找算法的数据结构，这个数据结构以某种方式指向数据、或者存储数据的引用，通过这个数据结构实现高级查找算法，这样就可以快速查找数据。
而这种数据结构就是索引。
索引按照结构划分为：线性索引、树形索引、多级索引。
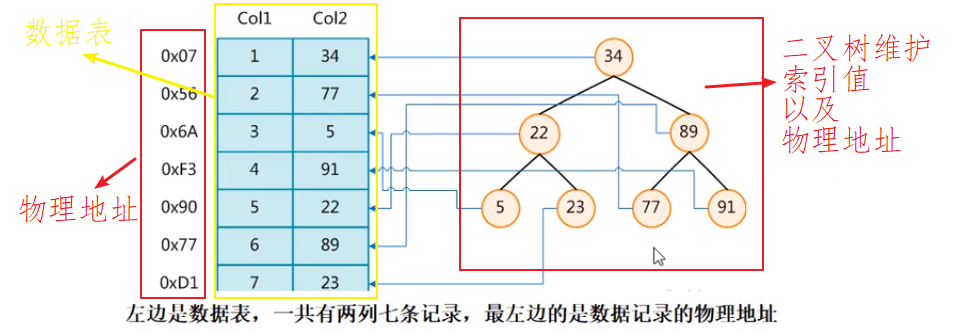
如下图所示数据结构：（树形索引，仅供参考，图片来源于网络）
使用二叉树维护数据的索引值以及数据的物理地址，使用二叉树可以在一定的时间复杂度内查找到数据，然后根据该数据的物理地址找到存储在表中的数据，从而实现快速查找。
2、线性索引（稠密索引、稀疏索引）
（1）什么是线性索引？
线性索引 指的是 将索引项组合成线性结构，也可称为索引表。
常见分类：稠密索引（密集索引）、稀疏索引（分块索引）、倒排索引。
（2）稠密索引（密集索引）
稠密索引 指的线性结构是：每个索引项 对应一个数据集（记录），记录在数据区（磁盘）中可以是无序的，但是所有索引项 是有序的（方便查找）。
但由于每个索引项占用的空间较大，若数据量较大时（每个索引项对应一个记录），占用空间会很大（可能无法一次在内存中读取，需要多次磁盘 I/O，降低查找性能）。
即 占用空间大、查找效率高。
如下图（图片来源于网络）：
左边索引表 中的索引项 按照关键码有序，可以使用 二分查找 或者其他高效查找算法，快速定位到对应的索引项，然后找到对应的 记录。
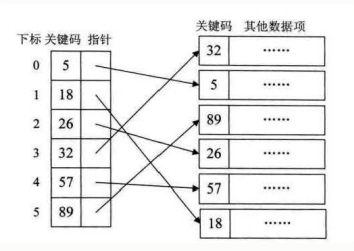
注：
前面介绍的 B+ 树的所有叶子节点可以看成是 稠密索引，其所有叶子节点 由链表连接，且叶子节点有序，可以应用上 稠密索引。
（3）稀疏索引（分块索引）
稠密索引 其每个索引项 对应一个记录，占用空间大。
稀疏索引 指的线性结构是：将数据集按照某种方式 分成若干个数据块，每个索引项 对应一个数据块。每个数据块可以包含多个数据（记录），这些数据之间可以是无序的。但 数据块之间是有序的（索引项有序）。
索引项无需保存 所有记录，只需要记录关键字即可，占用空间小。且索引项有序，可以快速定位到数据块。但是 数据块内没要求是有序的（维护有序序列需要付出一些代价），所以数据块中可能顺序查找（数据量较大时，查找效率较低）。
即 占用空间小、查找效率可能较低。
如下图（图片来源于网络）：
左边索引表 按照关键码有序，可以通过 二分查找 等算法快速定位到 数据块，然后在数据块中查找数据。
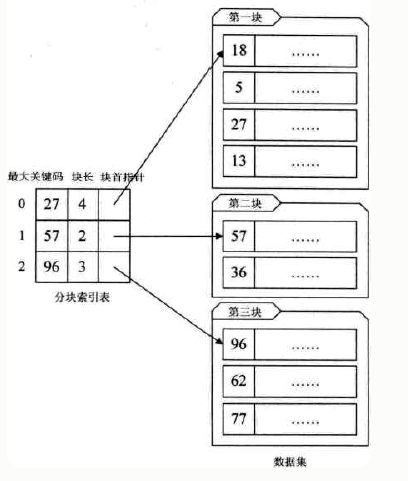
注：
前面介绍的 B+ 树中 非叶子节点 与 叶子节点 之间可以看成 稀疏索引，非叶子节点 仅保存 叶子节点的索引，叶子节点 保存 数据块。且此时 多个数据块之间 有序、每个数据块 之内也有序。
3、MySQL 索引底层数据结构
（1）底层数据结构
MySQL 底层数据结构，一般回答都是 B+ 树。
那么为什么选择 B+ 树？哈希、二叉树、B树 等结构不可以吗？
（2）为什么不使用 哈希表 作为索引？
【常用快速查找的数据结构有两种：】
哈希表：
比如 HashMap，其查找、添加、删除、修改的平均时间复杂度均为 O(1) 树：
比如 平衡二叉树，其查询、添加、删除、修改的平均时间复杂度均为O(logn) 【什么是哈希表？】
哈希表（Hash table 、散列表），是根据键（Key）直接访问数据（Value）的一种数据结构。
规则：
使用某种方式（映射函数）将键值（Key）映射到数组中的某个位置，并在此位置存放记录，用于加快查询速度。
映射函数 也称为 散列函数，存放记录的数组 称为 散列表。 理解：
使用 散列函数，将 键值（Key）转换为一个 整型数字，
然后再对数字进行转换（取模、与运算等），将其转为 数组对应的下标，并将 value 存储在该下标对应的存储空间中。
而进行查询操作时，再次对 Key 进行运算，转换为对应的数组下标，即可定位并获取 value 值（时间复杂度为 O(1)）。 【为什么不使用 哈希表？】
对于 单次写操作或者读操作 来说，哈希的速率比树快，但是为什么不用哈希表呢？ 可以想一下如果是排序或者范围查询的情况下，执行哈希是什么情况，很显然，哈希无法很快的进行范围查找（其数据都是无序的），查找范围 0~n 的情况下，会执行 n 次查找，也即时间复杂度为 O(n)。 而树（AVL树、B树、B+树等）是有序的（1、2 次查找即可），其时间复杂度仍可以保证在 O(logn)。 相比较之下，哈希肯定没有树的效率高，因此不会使用哈希这种数据结构作为索引。 【平衡二叉树时间复杂度 O(logn) 怎么来的？】
在树中查找一个数字时，第一次在树的第一层（根节点）判断，第二次在树的第二层判断，依次类推，树有多少层，就会进行多少次判断，即对于 k 层的树，最坏时间复杂度为O(k)。
所以只需要知道 n 个节点的树有多少层即可。 若为满二叉树（除叶子节点外，每个节点均有两个节点），则对于第一层，有一个节点（2^0），对于第二层有两个节点（2^1），依次类推对于第 k 层有 2^k-1（2 的 k-1 次方）。
所以 n = 2^0 + 2^1 + ... + 2^k-1，从而 k = log(n + 1)。
所以时间复杂度为 O(k) = O(logn) k 为树 层数，n 为树 节点数。
（3）为什么不使用二叉查找树（BST）、平衡二叉树（AVL）？
通过上面分析，可以使用树作为 索引（解决了范围、排序等问题），但是树有很多种类，比如：二叉查找树（BST）、平衡二叉树（AVL）、B 树、B+树等。应该选择哪种树作为索引呢？
对于二叉查找树，由于左子节点小于当前节点，右子节点大于当前节点，当一个数据是有序的时候，即数据要么递增，要么递减，此处二叉树出现如下图所示情况，相当于所有节点组成了链式结构，此时时间复杂度从 O(logn) 变为 O(n)。随着数据量增大，n 肯定非常大，这种情况下肯定不可取，舍弃。
二叉查找树可参考：https://www.cnblogs.com/l-y-h/p/13751459.html#_label5_8
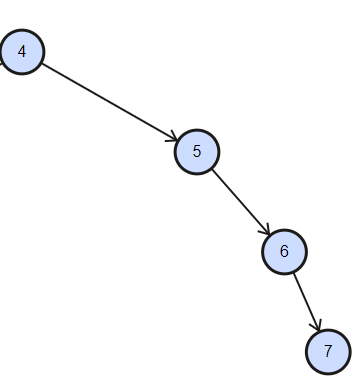
为了降低树的高度，引出了 平衡二叉树，其可以动态的维护树的高度，使任意一个节点左右子树高度差绝对值不大于 1。
对于平衡二叉查找树（AVL），新增节点时，会不断的调整节点位置以及树的高度。但随着数据量增大，树的高度也会增大，高度增大导致比较次数增多，若数据 无法一次读取到内存中，则每次比较前都得通过磁盘 IO 读取外存数据，导致磁盘 IO 增大，影响性能。
二叉平衡树可参考：https://www.cnblogs.com/l-y-h/p/13751459.html#_label5_9
通过上面分析，二叉查找树可能出现 只有左子树或者只有右子树的情况，当 数据量过大时，树的高度会变得很高，此时时间复杂度从 O(logn) 变为 O(n)，n 为 树的高度。
为了解决这种情况，可以使用平衡二叉查找树，其会在左右子树高度差大于 1 时对树节点进行旋转，保证树之间的高度差，从而解决二叉查找树的问题，但是数据量过大时，树的高度依旧会很大，增大磁盘 IO，影响性能。
所以为了解决树的高度问题，既然 二叉平衡树 不能满足需求，那就采用多叉平衡树，让一个节点保存多个数据（两个以上子树），进一步降低树的高度。从而引出 B 树、B+树。
（4）AVL 树、B树、B+树 举例：
构建树，并按照顺序插入 1 - 10，若查找 10 这个数，需要比较几次？
AVL 树构建如下：
树总高度为 4，而 10 在叶子节点，所以需要比较 4 次。
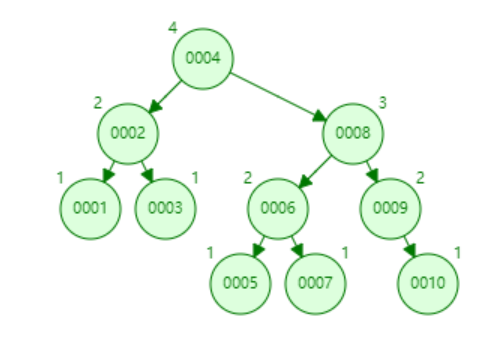
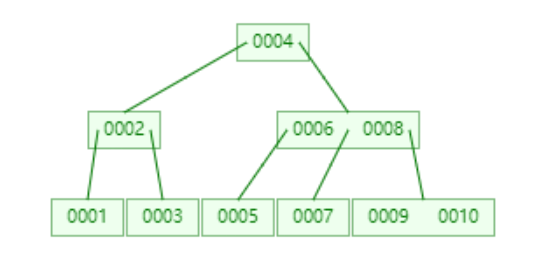
B 树构建如下：
树高度为 3 ，10 在叶子节点，此时只需要比较 3 次即可。
但对于 AVL，需要比较 4 次，随着数据量增大，B 树 明显比 AVL 高度低。
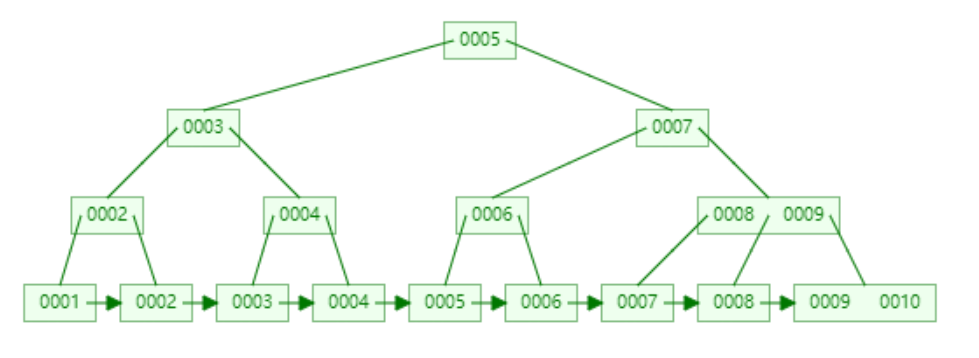
B+ 树构建如下：
树高度为 4，10 在叶子节点，此时需要比较 4 次。
B+ 树比 B 树更适合范围查找。
（5）为什么不使用 B 树 而使用 B+ 树？
通过上面分析，可以知道 平衡二叉树不能 满足实际的需求（数据量大时，树高度太大，且可能需要与磁盘进行多次 I/O 操作，查询效率低）。
那么 B 树能否满足需求呢？B 树的定义参考前面的分析。
理论上，B 树可以增加 每个节点保存的数据项 以及 节点的子节点数，并达到平衡树的条件，从而降低树的高度。但是不能无限制的 增大，B 树阶越大，那么每个节点 就可能成为 有序数组，则每次查找时效率反而会降低。
在 InnoDB 中，索引是存储元素的，一个表的数据 行数、列数 越多，那么相对应的索引文件就会很大。其不可能一次存放在内存中，需要经过多次磁盘 I/O。所以考虑 数据结构时，需要判断哪种数据结构更适合从磁盘中读取数据，减少磁盘 I/O 次数，从而提高磁盘 I/O 效率。
假定每次读取树的节点 都是 一次 磁盘 I/O，那么树的高度 将是决定 磁盘 I/O 的关键因素。
通过上面 AVL树、B树、B+树 的举例，可以看到 AVL 树由于每个节点只能存储两个元素，数据量大时，树的高度将会很大。
那么 B树、B+树 如何选择呢？
B 树由于 非叶子节点也会存放完整数据，则 B树 每个非叶子节点 存放的 元素总数 受到数据的影响，也即 每个非叶子节点 存放的 元素 较少，从而导致树的高度 也会很大。
B+ 树由于 非叶子节点 不存放完整数据（存放主键 + 指针），其完整数据存放在 叶子节点中，也即 非叶子节点 可以存放 更多的 元素，从而树的高度可以 很低。
通过上面分析，可以知道 B+ 树的高度很低，可以减少磁盘 I/O 的次数，提高执行效率。且 B+ 树所有叶子节点之间通过链表连接，其可以提高范围查询的效率。
所以 一般采用 B+ 树作为索引结构。
（6）总结
使用 B+ 树作为索引结构可以 减少磁盘 I/O 次数，提高查找效率。
B+ 树实际应用场景一般高度为 3（见下面分析，若一条记录为 1 KB，那么高度为 3 的 B+树 可以存储 2000 多万条数据）。
4、局部性原理、磁盘预读、B+树每个节点适合存多少数据
（1）局部性原理 与 磁盘预读
局部性原理 指的是 当一个数据被使用时，那么其附近的数据通常也会被使用。
在 InnoDB 中，数据存储在磁盘上，而直接操作磁盘 I/O 操作会很耗时（比操作内存中的数据慢），降低效率。
为了提高效率、降低磁盘 I/O 次数，在真正处理数据前 先要将数据 从磁盘中读取并加载到 内存中。
若每次只从 磁盘 读一条数据到 内存中，那么效率肯定很低。所以操作系统一般采用 磁盘预读的形式，一次读取 指定长度的数据进入内存（即使不需要使用到这么多数据，局部性原理）。此处指定长度称为 页，是操作系统操作数据的基本单位，操作系统中 页的大小一般为 4KB。
（2）B+树中 一个节点存储多少数据合适？
进行磁盘预读时，将数据划分成若干个页，以 页 作为 磁盘 与 内存 交互的基本单位，InnoDB 默认页大小是 16 KB（类似于操作系统页的定义，若操作系统页大小为 4KB，那么 InnoDB 中 1页 等于 操作系统 4页），即每次最少从磁盘中读取 16KB 数据到内存，最少从 内存写入 16KB 数据到磁盘。
B+ 树每个节点 存放 一页、或者 页的倍数比较合适。（假设每次读取节点均会经过磁盘 I/O）
以一页为例，如果节点存储小于 一页，那么读取这个节点时仍然会读出一页，从而造成资源的浪费。而如果节点存储大于 一页小于二页，那么读取这个节点时将会读出 二页，同样也会造成资源的浪费。所以，一般 B+树 节点存放数据为 一页 或者 页的倍数。
【查看 InnoDB 默认页大小：】
SHOW GLOBAL STATUS like 'Innodb_page_size';
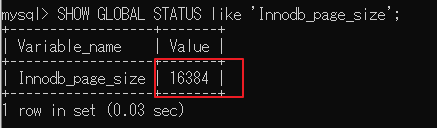
（3）为什么 InnoDB 设置默认页大小为 16KB？而不是 32KB？
【首先明确一点：】
B+ 树 非叶子节点存储的是 主键（关键字）+ 指针（指向叶子节点）。
B+ 树 叶子节点存储的是 数据（真实的数据记录）。
假设每次读取一个节点均会执行一次磁盘 I/O，即每个节点大小为页的大小。 【以节点大小为 16KB 为例：】
假设一行数据大小为 1KB，那么一个叶子节点能保存 16 条记录。
假设非叶子节点主键为 bigint 类型，那么长度为 8B，而指针在 InnoDB 中大小为 6B，即一个非叶子节点能保存 16KB / 14B = 1170 个数据（主键 + 指针）。
那么对于 高度为 2 的 B+树，能存储记录数为： 1170 * 16 = 18720 条。
对于 高度为 3 的 B+树，能存储记录数为：1170 * 1170 * 16 = 21902400 条。 也就是说，若页大小为 16KB，那么高度为 3 的 B+ 树就能支持 2千万的数据存储。
当然若页大小更大，树的高度也会低，但是一般没有必要去修改。 读取一个节点需要经过一次磁盘 I/O，那么根据主键 只需要 1-3 次磁盘 I/O 即可查询到数据，能满足绝大部分需求。
5、MySQL 表存储引擎 MyISAM 与 InnoDB 区别？
（1）MySQL 采用 插件式的表存储引擎 管理数据，基于表而非基于数据库。在 MySQL 5.5 版本前默认使用 MyISAM 为默认存储引擎，在 5.5 版本后采用 InnoDB 作为默认存储引擎。
（2）MyISAM 不支持外键、不支持事务，支持表级锁（即每次操作均会对整个表加锁，不适合高并发操作）。会存储表的总行数，占用表空间小，多用于 读操作多 的场合。只缓存索引但不缓存真实数据。
（3）InnoDB 支持外键、支持事务，支持行级锁。不存储表的总行数，占用表空间大，多用于 写操作多 的场合。缓存索引的同时缓存真实数据，对内存要求较高（内存大小影响性能）。
（4）底层索引实现：
MyISAM 使用 B+树作为 索引结构，但是其 索引文件 与 数据文件是 分开的，其叶子节点 存放的是 数据记录的地址，也即根据索引文件 找到 对应的数据记录的地址后，再去获取相应的数据。
InnoDB 使用 B+树作为 索引结构，但是其 索引文件本身就是 数据文件，其叶子节点 存放的就是 完整的数据记录。InnoDB 必须要有主键，如果没有显示指定，系统会默认选择一个能够唯一标识数据记录的列作为主键，如果不存在这样的键，系统会给表生成一个隐含字段作为主键。
注：
InnoDB 中一般使用 自增的 id 作为主键，每插入一条记录，相当于增加一个节点，如果主键是顺序的，那么直接添加在上一个记录后即可，若当前页满后，在新的页中继续存储。
若主键无序，那么在插入数据的过程中，可能或出现在 所有叶子节点任意位置，若出现在所有叶子节点头部，那么将会导致所有叶子节点均向后移一位，涉及到 页的分裂以及数据的移动，是一种耗时操作、且造成大量内存碎片，影响效率。
6、索引的代价 与 选择
（1）索引的代价：
空间上：
一个索引 对应一颗 B+ 树，树的每个节点都是一个数据页，一个数据页占用大小为 16KB 的存储空间，数据量越大，占用的空间也就越大。
时间上：
索引会根据数据进行排序，当对数据表数据进行 增、删、改 操作时，相应的 B+ 树索引也要去维护，会消耗时间 进行 记录移动、页面分裂、页面回收 等操作，并维护 数据有序。
（2）索引的选择：
索引的选择性：
指的是 不重复索引值（基数）与 表记录总数 的比值（选择性 = 不重复索引值 / 表记录总数）。
范围为 (0, 1]，选择性 越大，即不重复索引值 越多，则建立索引的价值越大。
选择性越小，即 重复索引值 越多，那么索引的意义不大。
索引选择：
索引列 类型应尽量小。
主键自增。
三、图
1、图的基本介绍
（1）图是什么？
图用来描述 多对多关系 的一种数据结构。
上一篇介绍了 一对一 的数据结构（比如：单链表、队列、栈等）以及 一对多的数据结构（比如：树），参考链接：https://www.cnblogs.com/l-y-h/p/13751459.html 。
为了解决 多对多 关系，此处引入了 图 这种数据结构。
（2）图的基本概念
图是一种数据结构，其每个节点可以具有 零个 或者 多个相邻的元素。
两个节点之间的连接称为边（edge），节点可称为顶点（vertex）。
从一个节点到另一个节点 所经过的边称为 路径。
即 图由若干个顶点以及 顶点之间的边 组合而成。
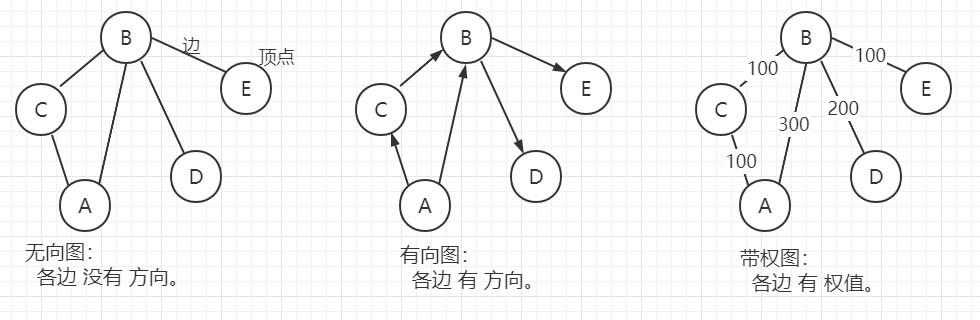
图按照边可以分为：
无向图。指的是 顶点之间的连接（边） 没有方向的图。
有向图。指的是 边 有方向的图。
带权图。指的是 边 带有权值的图。
（3）图的表示方式
图的表示形式一般有两种：邻接矩阵（二维数组表示）、邻接表（链表）。
邻接矩阵：
使用 一维数组 记录图中 顶点数据，使用 二维数组 记录图中 顶点之间的相邻关系（边）。对于 n 个顶点的图，使用 n*n 的二维数组记录 边的关系。
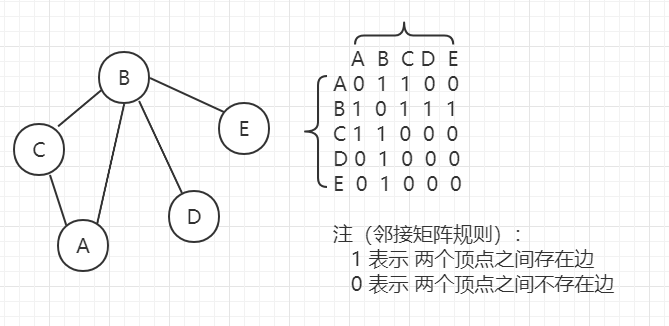
邻接表：
使用 数组 + 链表的形式 记录 各顶点 以及顶点之间的 相邻关系（只记录存在的边）。
使用 一维数组 记录图中 顶点数据，使用链表记录 存在的边。
邻接表 与 邻接矩阵区别：
邻接矩阵中 需要为 每个顶点 记录 n 个边，其中很多边不存在（无需记录），造成空间的浪费。
邻接表只 记录存在的边，不会造成空间的浪费。
（4）使用 邻接矩阵 形式构建 无向图：
【构建思路：】
使用 一维数组 记录 图的顶点数据。
使用 二维数组 记录 图的各顶点的联系（边，其中 1 表示存在边，0 表示不存在边）。 【代码实现：】
package com.lyh.chart; import java.util.ArrayList;
import java.util.Arrays;
import java.util.List; /**
* 使用 邻接矩阵 形式构建无向图
*/
public class UndirectedGraph {
private List<String> vertexs; // 用于保存 无向图 的顶点数据（可以使用一维数组）
private int[][] edges; // 用于保存 无向图 中各顶点之间的关系，1 表示两顶点之间存在边，0 表示不存在边
private int numberOfEdges; // 用于记录 无向图中边的个数 /**
* 根据 顶点个数 进行初始化
* @param number 顶点个数
*/
public UndirectedGraph(int number) {
vertexs = new ArrayList<>(number); // 用于记录顶点
edges = new int[number][number]; // 用于记录顶点之间的关系
numberOfEdges = 0; // 用于记录边的个数
} /**
* 添加顶点
* @param vertex 顶点
*/
public void insertVertex(String vertex) {
vertexs.add(vertex);
} /**
* 添加边
* @param row 行
* @param column 列
* @param value 值（1 表示存在边，0表示不存在边）
*/
public void insertEdge(int row, int column, int value) {
edges[row][column] = value; // 设置边
edges[column][row] = value; // 设置边，对称
numberOfEdges++; // 边总数加 1
} /**
* 返回边的总数
* @return 边的总数
*/
public int getNumberOfEdges() {
return numberOfEdges;
} /**
* 返回顶点的总数
* @return 顶点总数
*/
public int getNumberOfVertex() {
return vertexs.size();
} /**
* 返回 下标对应的顶点数据
* @param index 顶点下标
* @return 顶点数据
*/
public String getValueByIndex(int index) {
return vertexs.get(index);
} /**
* 输出邻接矩阵
*/
public void showGraph() {
for (int[] row : edges) {
System.out.println(Arrays.toString(row));
}
} public static void main(String[] args) {
// 初始化无向图
UndirectedGraph undirectedGraph = new UndirectedGraph(5);
// 插入顶点数据
String[] vertexs = new String[]{"A", "B", "C", "D", "E"};
for (String vertex : vertexs) {
undirectedGraph.insertVertex(vertex);
}
// 插入边
undirectedGraph.insertEdge(0, 1, 1); // A-B
undirectedGraph.insertEdge(0, 2, 1); // A-C
undirectedGraph.insertEdge(1, 2, 1); // B-C
undirectedGraph.insertEdge(1, 3, 1); // B-D
undirectedGraph.insertEdge(1, 4, 1); // B-E // 输出
System.out.println("无向图顶点总数为： " + undirectedGraph.getNumberOfVertex());
System.out.println("无向图边总数为： " + undirectedGraph.getNumberOfEdges());
System.out.println("无向图第 3 个顶点为： " + undirectedGraph.getValueByIndex(2));
System.out.println("无向图 邻接矩阵为： ");
undirectedGraph.showGraph();
}
} 【输出结果为：】
无向图顶点总数为： 5
无向图边总数为： 5
无向图第 3 个顶点为： C
无向图 邻接矩阵为：
[0, 1, 1, 0, 0]
[1, 0, 1, 1, 1]
[1, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
（5）图的遍历方式：
图的遍历，即对顶点的访问，一般遍历顶点有两种策略：DFS、BFS。
DFS 为深度优先遍历，可以联想到 树的 先序、中序、后序 遍历。即 纵向访问 节点。
BFS 为广度优先遍历，可以联想到 树的 顺序（层序）遍历，即 横向分层 访问 节点。
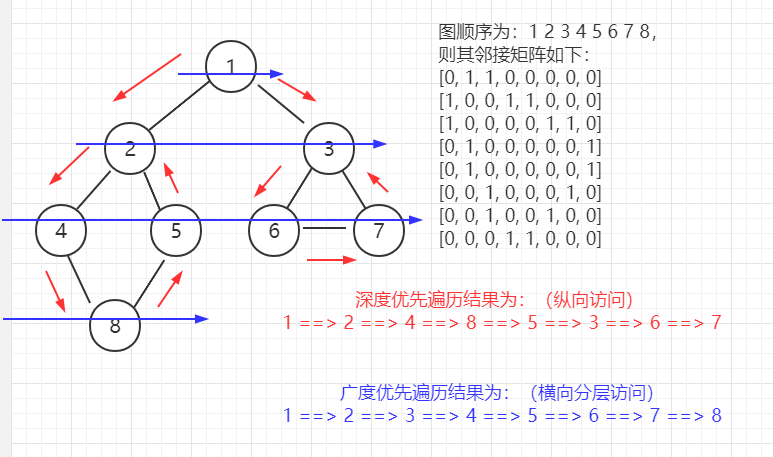
2、深度优先遍历（DFS）
（1）DFS
DFS 指的是 Depth First Search，即 深度优先搜索。
其从一个节点出发，优先访问该节点的第一个邻接节点，并将此邻接节点作为新的节点，继续访问其第一个邻接节点（为了防止重复访问同一节点，可以将节点分为 已访问、未访问 两种状态，若节点已访问，则跳过该节点）。
深度优先搜索是一个递归的过程（可以使用栈模拟递归实现），每次访问当前节点的第一个邻接节点。
（2）DFS 步骤 与 代码实现：
【步骤：】
Step1：访问初始节点 start，标记该节点 start 已访问。
Step2：查找节点 start 的第一个邻接节点 neighbor。
Step2.1：若 neighbor 不存在，则返回 Step1，且从 start 下一个节点继续执行。
Step2.2：若 neighbor 存在，且未被访问，则返回 Step1，且将 neighbor 视为新的 start 执行。
Step2.3：若 neighbor 存在，且已被访问，则返回 Step2，且从 neighbor 下一个节点继续执行。 【举例：】
图的 邻接矩阵表示如下：,图各顶点 按照顺序为 A B C D E。
A B C D E
A [0, 1, 1, 0, 0]
B [1, 0, 1, 1, 1]
C [1, 1, 0, 0, 0]
D [0, 1, 0, 0, 0]
E [0, 1, 0, 0, 0]
注：
1 表示两个顶点间存在边，0 表示不存在边。 则遍历过程如下：（整个过程是纵向的）
Step1：从 A 开始遍历，将 A 标记为 已访问。找到 A 的 第一个邻接节点 B。
Step2：B 未被访问，将 B 视为新的节点开始遍历，将 B 标记为已访问，找到 B 的第一个邻接节点 A。
Step3：A 被访问过，继续查找 B 下一个邻接节点为 C。
Step4：C 未被访问过，将 C 视为新节点开始遍历，将 C 标记为已访问，找到 C 的第一个邻接节点 A。
Step5：A 被访问，继续查找 C 下一个邻接节点为 B，B 也被访问，继续查找，C 没有邻接节点，回退到上一层 B。
Step6：继续查找 B 下一个邻接节点为 D，将 D 标记已访问，同理可知 D 没有 未被访问的邻接顶点，回退到上一层 B。
Step7：查找 B 下一个邻接节点为 E，将 E 标记已访问，至此遍历完成。
即顺序为：A -> B -> C -> D -> E 【代码实现：】
package com.lyh.chart; import java.util.ArrayList;
import java.util.Arrays;
import java.util.List; /**
* 使用 邻接矩阵 形式构建无向图
*/
public class UndirectedGraph {
private List<String> vertexs; // 用于保存 无向图 的顶点数据（可以使用一维数组）
private int[][] edges; // 用于保存 无向图 中各顶点之间的关系，1 表示两顶点之间存在边，0 表示不存在边
private int numberOfEdges; // 用于记录 无向图中边的个数
private boolean[] isVisit; // 用于记录 顶点是否被访问，true 表示已访问 /**
* 根据 顶点个数 进行初始化
* @param number 顶点个数
*/
public UndirectedGraph(int number) {
vertexs = new ArrayList<>(number); // 用于记录顶点
edges = new int[number][number]; // 用于记录顶点之间的关系
numberOfEdges = 0; // 用于记录边的个数
isVisit = new boolean[number]; // 用于记录顶点是否被访问
} /**
* 添加顶点
* @param vertex 顶点
*/
public void insertVertex(String vertex) {
vertexs.add(vertex);
} /**
* 添加边
* @param row 行
* @param column 列
* @param value 值（1 表示存在边，0表示不存在边）
*/
public void insertEdge(int row, int column, int value) {
edges[row][column] = value; // 设置边
edges[column][row] = value; // 设置边，对称
numberOfEdges++; // 边总数加 1
} /**
* 返回边的总数
* @return 边的总数
*/
public int getNumberOfEdges() {
return numberOfEdges;
} /**
* 返回顶点的总数
* @return 顶点总数
*/
public int getNumberOfVertex() {
return vertexs.size();
} /**
* 返回 下标对应的顶点数据
* @param index 顶点下标
* @return 顶点数据
*/
public String getValueByIndex(int index) {
return vertexs.get(index);
} /**
* 输出邻接矩阵
*/
public void showGraph() {
for (int[] row : edges) {
System.out.println(Arrays.toString(row));
}
} /**
* 获取下一个顶点的下标
* @param row 行
* @param column 列
* @return 下一个邻接顶点的下标（-1 表示不存在下一个邻接顶点）
*/
public int getNeighborVertexIndex(int row, int column) {
for (int index = column + 1; index < vertexs.size(); index++) {
if (edges[row][index] != 0) {
return index;
}
}
return -1;
} /**
* 返回当前顶点 的第一个邻接顶点的下标
* @param index 当前顶点下标
* @return 第一个邻接顶点的下标（-1 表示不存在邻接顶点）
*/
public int getFirstVertextIndex(int index) {
return getNeighborVertexIndex(index, -1);
} /**
* 深度优先遍历
*/
public void dfs() {
// 未被访问的顶点，进行深度优先遍历
for (int index = 0; index < vertexs.size(); index++) {
if (!isVisit[index]) {
dfs(index);
}
}
} /**
* 深度优先遍历
* @param index 顶点下标
*/
private void dfs(int index) {
// 输出当前顶点数据
System.out.print(getValueByIndex(index) + " ==> ");
// 标记当前顶点为 已访问
isVisit[index] = true;
// 获取当前顶点第一个邻接顶点下标
int neighborIndex = getFirstVertextIndex(index);
// 当下一个邻接顶点存在时
while(neighborIndex != -1) {
// 若邻接顶点未被访问，则递归遍历
if (!isVisit[neighborIndex]) {
dfs(neighborIndex);
} else {
// 若邻接顶点已被访问，则访问当前邻接顶点的下一个邻接顶点
neighborIndex = getNeighborVertexIndex(index, neighborIndex);
}
}
} public static void main(String[] args) {
// 初始化无向图
UndirectedGraph undirectedGraph = new UndirectedGraph(5);
// 插入顶点数据
String[] vertexs = new String[]{"A", "B", "C", "D", "E"};
for (String vertex : vertexs) {
undirectedGraph.insertVertex(vertex);
}
// 插入边
undirectedGraph.insertEdge(0, 1, 1); // A-B
undirectedGraph.insertEdge(0, 2, 1); // A-C
undirectedGraph.insertEdge(1, 2, 1); // B-C
undirectedGraph.insertEdge(1, 3, 1); // B-D
undirectedGraph.insertEdge(1, 4, 1); // B-E // 输出
System.out.println("无向图顶点总数为： " + undirectedGraph.getNumberOfVertex());
System.out.println("无向图边总数为： " + undirectedGraph.getNumberOfEdges());
System.out.println("无向图第 3 个顶点为： " + undirectedGraph.getValueByIndex(2));
System.out.println("无向图 邻接矩阵为： ");
undirectedGraph.showGraph(); System.out.println("深度优先遍历结果为： ");
undirectedGraph.dfs();
}
} 【输出结果：】
无向图顶点总数为： 5
无向图边总数为： 5
无向图第 3 个顶点为： C
无向图 邻接矩阵为：
[0, 1, 1, 0, 0]
[1, 0, 1, 1, 1]
[1, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
深度优先遍历结果为：
A ==> B ==> C ==> D ==> E ==>
3、广度优先遍历（BFS）
（1）BFS
BFS 指的是 Broad First Search，即广度优先搜索。
其类似于 分层搜索的过程，依次访问各层 的节点。可以使用队列来记录 访问过的节点的顺序，用于按照该顺序来访问 这些节点的邻接节点。
（2）BFS 步骤、代码实现
【步骤：】
Step1：访问初始节点 start，并标记为 已访问，start 入队列。
Step2：循环取出队列，若队列为空，则结束循环，否则执行下面步骤。
Step3：取得队列头部节点，即为 first，并查找 first 的第一个邻接节点 neighbor。
Step3.1：若 neighbor 不存在，则返回 Step2，再取出队列 新的头节点。
Step3.2：若 neighbor 存在，且未被访问，则将其标记为 已访问并入队列。
Step3.3：若 neighbor 存在，且已被访问，则返回 Step3，并查找 neighbor 的下一个节点。
注：
Step3 将某一层 未访问的节点 入队列，当该层顶点全部被访问时，执行 Step2，
从队列中取出 头部节点，即为 新的层，并开始查找未被访问的节点入队列。 【举例：】
图的 邻接矩阵表示如下：,图各顶点 按照顺序为 A B C D E。
A B C D E
A [0, 1, 1, 0, 0]
B [1, 0, 1, 1, 1]
C [1, 1, 0, 0, 0]
D [0, 1, 0, 0, 0]
E [0, 1, 0, 0, 0]
注：
1 表示两个顶点间存在边，0 表示不存在边。 则遍历过程如下：（整个过程是横向分层的）
Step1：从 A 开始，将其标记为 已访问，将 A 存入队列末尾。
Step2：取出队列头部元素为 A，查找其邻接节点为 B，B 未被访问将其入队列、并标记为 已访问。
Step3：继续查找 A 下一个邻接节点为 C，C 为被访问将其入队列、并标记为 已访问。
Step4：A 层遍历结束，取出队列头部为元素为 B，即开始访问 B 层。
Step5：B 层未被访问的节点 依次入队列并标记为已访问。即 D、E 入队列。
Step6：同理依次取出队列头部元素 C、D、E，直至遍历完成。
即顺序为：A -> B -> C -> D -> E 【代码实现：】
package com.lyh.chart; import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List; /**
* 使用 邻接矩阵 形式构建无向图
*/
public class UndirectedGraph {
private List<String> vertexs; // 用于保存 无向图 的顶点数据（可以使用一维数组）
private int[][] edges; // 用于保存 无向图 中各顶点之间的关系，1 表示两顶点之间存在边，0 表示不存在边
private int numberOfEdges; // 用于记录 无向图中边的个数
private boolean[] isVisit; // 用于记录 顶点是否被访问，true 表示已访问 /**
* 根据 顶点个数 进行初始化
* @param number 顶点个数
*/
public UndirectedGraph(int number) {
vertexs = new ArrayList<>(number); // 用于记录顶点
edges = new int[number][number]; // 用于记录顶点之间的关系
numberOfEdges = 0; // 用于记录边的个数
isVisit = new boolean[number]; // 用于记录顶点是否被访问
} /**
* 添加顶点
* @param vertex 顶点
*/
public void insertVertex(String vertex) {
vertexs.add(vertex);
} /**
* 添加边
* @param row 行
* @param column 列
* @param value 值（1 表示存在边，0表示不存在边）
*/
public void insertEdge(int row, int column, int value) {
edges[row][column] = value; // 设置边
edges[column][row] = value; // 设置边，对称
numberOfEdges++; // 边总数加 1
} /**
* 返回边的总数
* @return 边的总数
*/
public int getNumberOfEdges() {
return numberOfEdges;
} /**
* 返回顶点的总数
* @return 顶点总数
*/
public int getNumberOfVertex() {
return vertexs.size();
} /**
* 返回 下标对应的顶点数据
* @param index 顶点下标
* @return 顶点数据
*/
public String getValueByIndex(int index) {
return vertexs.get(index);
} /**
* 输出邻接矩阵
*/
public void showGraph() {
for (int[] row : edges) {
System.out.println(Arrays.toString(row));
}
} /**
* 获取下一个顶点的下标
* @param row 行
* @param column 列
* @return 下一个邻接顶点的下标（-1 表示不存在下一个邻接顶点）
*/
public int getNeighborVertexIndex(int row, int column) {
for (int index = column + 1; index < vertexs.size(); index++) {
if (edges[row][index] != 0) {
return index;
}
}
return -1;
} /**
* 返回当前顶点 的第一个邻接顶点的下标
* @param index 当前顶点下标
* @return 第一个邻接顶点的下标（-1 表示不存在邻接顶点）
*/
public int getFirstVertextIndex(int index) {
return getNeighborVertexIndex(index, -1);
} /**
* 广度优先遍历
*/
public void bfs() {
// 未被访问的顶点，进行广度优先遍历
for (int index = 0; index < vertexs.size(); index++) {
if (!isVisit[index]) {
bfs(index);
}
}
} /**
* 广度优先遍历
* @param index 顶点下标
*/
private void bfs(int index) {
// 输出当前顶点数据
System.out.print(getValueByIndex(index) + " ==> ");
// 用于记录访问的顶点
LinkedList<Integer> queue = new LinkedList<>();
int firstIndex; // 用于记录队列的头部节点
int neighborIndex; // 用于记录邻接节点
isVisit[index] = true; // 标记当前节点已被访问
queue.addLast(index); // 当前节点入队列
// 队列不空时
while(!queue.isEmpty()) {
// 取出队列头节点
firstIndex = queue.removeFirst();
// 找到邻接节点
neighborIndex = getFirstVertextIndex(index);
while(neighborIndex != -1) {
if(!isVisit[neighborIndex]) {
// 输出当前顶点数据
System.out.print(getValueByIndex(neighborIndex) + " ==> ");
isVisit[neighborIndex] = true;
queue.addLast(neighborIndex);
} else {
neighborIndex = getNeighborVertexIndex(firstIndex, neighborIndex);
}
}
}
} public static void main(String[] args) {
// 初始化无向图
UndirectedGraph undirectedGraph = new UndirectedGraph(5);
// 插入顶点数据
String[] vertexs = new String[]{"A", "B", "C", "D", "E"};
for (String vertex : vertexs) {
undirectedGraph.insertVertex(vertex);
}
// 插入边
undirectedGraph.insertEdge(0, 1, 1); // A-B
undirectedGraph.insertEdge(0, 2, 1); // A-C
undirectedGraph.insertEdge(1, 2, 1); // B-C
undirectedGraph.insertEdge(1, 3, 1); // B-D
undirectedGraph.insertEdge(1, 4, 1); // B-E // 输出
System.out.println("无向图顶点总数为： " + undirectedGraph.getNumberOfVertex());
System.out.println("无向图边总数为： " + undirectedGraph.getNumberOfEdges());
System.out.println("无向图第 3 个顶点为： " + undirectedGraph.getValueByIndex(2));
System.out.println("无向图 邻接矩阵为： ");
undirectedGraph.showGraph(); System.out.println("广度优先遍历结果为： ");
undirectedGraph.bfs();
}
} 【输出结果：】
无向图顶点总数为： 5
无向图边总数为： 5
无向图第 3 个顶点为： C
无向图 邻接矩阵为：
[0, 1, 1, 0, 0]
[1, 0, 1, 1, 1]
[1, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
广度优先遍历结果为：
A ==> B ==> C ==> D ==> E ==>
四、常用五种算法
1、二分查找算法（递归与非递归）
（1）二分查找
二分查找是一个效率较高的查找方法。其要求必须采用 顺序存储结构 且 存储数据有序。
每次查找数据时 根据 待查找数据 将总数据 分为两部分（一部分小于 待查找数据，一部分大于 待查找数据），设折半次数为 x，则 2^x = n，即折半次数为 x = logn，时间复杂度为 O(logn)。
（2）递归、非递归实现 二分查找
【代码实现：】
package com.lyh.algorithm; /**
* 二分查找、递归 与 非递归 实现
*/
public class BinarySearch {
public static void main(String[] args) {
// 构建升序序列
int[] arrays = new int[]{13, 27, 38, 49, 65, 76, 97};
// 设置待查找数据
int key = 27;
// 递归二分查找
int index = binarySearch(arrays, 0, arrays.length - 1, key);
if (index != -1) {
System.out.println("查找成功，下标为： " + index);
} else {
System.out.println("查找失败");
} // 非递归二分查找
int index2 = binarySearch2(arrays, 0, arrays.length - 1, key);
if (index2 != -1) {
System.out.println("查找成功，下标为： " + index2);
} else {
System.out.println("查找失败");
}
} /**
* 折半查找，返回元素下标（递归查找，数组升序）
* @param arrays 待查找数组
* @param left 最左侧下标
* @param right 最右侧下标
* @param key 待查找数据
* @return 查找失败返回 -1，查找成功返回元素下标 0 ~ n
*/
public static int binarySearch(int[] arrays, int left, int right, int key) {
if (left <= right) {
// 获取中间下标
int middle = (left + right) / 2;
// 查找成功返回数据
if (arrays[middle] == key) {
return middle;
}
// 待查找数据 小于 中间数据，则从 左半部分数据进行查找
if (arrays[middle] > key) {
return binarySearch(arrays, left, middle - 1, key);
}
// 待查找数据 大于 中间数据，则从 右半部分数据进行查找
if (arrays[middle] < key) {
return binarySearch(arrays, middle + 1, right, key);
}
}
return -1;
} /**
* 折半查找，返回元素下标（非递归查找，数组升序）
* @param arrays 待查找数组
* @param left 最左侧下标
* @param right 最右侧下标
* @param key 待查找数据
* @return 查找失败返回 -1，查找成功返回元素下标 0 ~ n
*/
public static int binarySearch2(int[] arrays, int left, int right, int key) {
while(left <= right) {
// 获取中间下标
int middle = (left + right) / 2;
// 查找成功返回数据
if (arrays[middle] == key) {
return middle;
}
// 待查找数据 小于 中间数据，则从 左半部分数据进行查找
if (arrays[middle] > key) {
right = middle - 1;
} else {
// 待查找数据 大于 中间数据，则从 右半部分数据进行查找
left = middle + 1;
}
}
return -1;
}
} 【输出结果：】
查找成功，下标为： 1
查找成功，下标为： 1
2、分治算法（汉诺塔问题）
（1）分治算法：
分治法 简单理解就是 分而治之，其将一个复杂的问题 分成 两个或者 若干个 相同或者 类似的 子问题，子问题 又可进一步划分为 若干个更小的子问题，直至 子问题可以很简单的求解，然后将 所有简单的子问题解合并，即可得到原问题的解。
【分治算法常见实现：】
归并排序、快速排序、汉诺塔问题等。 【分治算法基本步骤：】
Step1：分解，将原问题 分解成 若干个 规模小、相互独立、与原问题类似的 子问题。
Step2：求解，对于简单的子问题直接求解，否则递归求解各个子问题。
Step3：合并，将各个子问题的解合并为原问题的解。
（2）汉诺塔代码实现
【汉诺塔问题：】
有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。
开始时所有盘子 按照自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。
将所有盘子 从 第一根柱子上 移动到 第三根柱子上。
移动圆盘时受到以下限制:
每次只能移动一个盘子;
盘子只能从柱子顶端滑出移到下一根柱子;
盘子只能叠在比它大的盘子上。 【汉诺塔分析：】
假设三个柱子分为为：A B C，盘子最开始放置在 A，需要从 A 将其移动到 C。
若只有一个盘子：
直接从 A 移动到 C。 若有 2 个盘子：
则先将第一个盘子从 A 移动到 B，
再将第二个盘子从 A 移动到 C，
最后再将 第一个盘子从 B 移动到 C。 若有 3 个盘子：
先将第 1 个盘子从 A 移动到 C
再将第 2个盘子从 A 移动到 B
再将第 1 个盘子从 C 移动到 B
再将第 3个盘子从 A 移动到 C
再将第 1 个盘子从 B 移动到 A
再将第 2个盘子从 B 移动到 C
最后第 1 个盘子从 A 移动到 C 同理，第 4、5...n 个盘子。
可以将 盘子分为两部分，一部分为 最底下的盘子（最大的盘子），一部分为 其余盘子。
先将其余盘子从 A 移动到 B 柱子上，再将 最大盘子从 A 移动到 C 柱子上，最后将 其余盘子从 B 移动到 C 柱子上。
注：
由于其余盘子数量可能大于 2，所以需要递归进行分治处理。
比如：
3 个盘子，原柱子为 A，目标柱子为 C，可借助中间柱子 B，将其视为 (A, B, C)。
将盘子从上到下分为两部分，第 1、2 个盘子为其余盘子，第 3 个盘子为最大盘子。
若其余盘子数量大于 2，又可以拆分成更小的盘子进行操作。
首先将 其余盘子 从 A 移动到 B，原柱子为 A，目标为 B，可借助中间柱子 C，将其视为 (A, C, B)。
然后将 最大盘子 从 A 移动到 C，直接移动。
最后将 其余盘子 从 B 移动到 C，原柱子为 B，目标为 C，可借助中间柱子 A，将其视为 (B, A, C)。 【代码实现：】
package com.lyh.algorithm; import java.util.ArrayList;
import java.util.List; public class HanoiTower {
public static void main(String[] args) {
// 打印汉诺塔盘子移动过程
hanoiTower(3, "A", "B", "C");
System.out.println("===========================\n"); // 打印汉诺塔结果
List<Integer> origin = new ArrayList<>();
origin.add(2);
origin.add(1);
origin.add(0);
List<Integer> middle = new ArrayList<>();
List<Integer> target = new ArrayList<>();
System.out.println("原汉诺塔为： ");
System.out.println("原柱子： " + origin);
System.out.println("中间柱子： " + middle);
System.out.println("目标柱子： " + target);
hanoiTower(origin, middle, target);
System.out.println("移动后的汉诺塔为： ");
System.out.println("原柱子： " + origin);
System.out.println("中间柱子： " + middle);
System.out.println("目标柱子： " + target);
} /**
* 汉诺塔问题，将盘子从原始柱子 A 移动到 目标柱子 C，可借助中间柱子 B。
* 打印出移动流程。
* @param num 盘子总数
* @param a A 原始柱子
* @param b B 中间柱子
* @param c C 目标柱子
*/
public static void hanoiTower(int num, String a, String b, String c) {
// 只剩 1 个盘子时，直接从 A 移动到 C
if (num == 1) {
System.out.println("第 1 个盘子从 " + a + " 移动到 " + c);
return;
}
// 盘子数 大于 2 时，将盘子视为两个部分，一个为 最大的盘子，另一个为 其余盘子
// 先将其余盘子 移动到中间柱子上，即从 A 移动到 B，移动过程中使用到 C，此时 原始柱子为 A，目标柱子为 B，中间柱子为 C
hanoiTower(num - 1, a, c, b);
// 再将最大的盘子从 A 移动到 C
System.out.println("第 " + num + "个盘子从 " + a + " 移动到 " + c);
// 最后将其余盘子 从中间柱子移动到目标柱子上，即从 B 移动到 C，移动过程中使用到 A，此时 原始柱子为 B，目标柱子为 C，中间柱子为 A
hanoiTower(num - 1, b, a, c);
} /**
* 将盘子从 origin 移动到 target
* @param origin 原始柱子
* @param middle 中间柱子
* @param target 目标柱子
*/
public static void hanoiTower(List<Integer> origin, List<Integer> middle, List<Integer> target) {
move(origin.size(), origin, middle, target);
} private static void move(int num, List<Integer> origin, List<Integer> middle, List<Integer> target) {
// 只剩 1 个盘子时，直接从原始柱子 origin 移动到目标柱子 target
if (num == 1) {
target.add(origin.remove(origin.size() - 1));
return;
}
// 将 其余盘子从原始柱子 origin 移动到中间柱子 middle 上，此时可将 target 视为中间柱子
move(num - 1, origin, target, middle);
// 将 最大盘子从原始柱子 origin 直接移动到 目标柱子 target 上。
target.add(origin.remove(origin.size() - 1));
// 将 其余盘子从中间柱子 middle 移动到目标柱子 target 上，此时可将 origin 视为中间柱子
move(num - 1, middle, origin, target);
} /**
* 取巧思路，非算法实现（博大家一笑）
* @param origin 原柱子
* @param middle 中间柱子
* @param target 目标柱子
*/
public static void hanoiTower2(List<Integer> origin, List<Integer> middle, List<Integer> target) {
target.addAll(origin);
origin.clear();
}
} 【输出结果：】
第 1 个盘子从 A 移动到 C
第 2个盘子从 A 移动到 B
第 1 个盘子从 C 移动到 B
第 3个盘子从 A 移动到 C
第 1 个盘子从 B 移动到 A
第 2个盘子从 B 移动到 C
第 1 个盘子从 A 移动到 C
=========================== 原汉诺塔为：
原柱子： [2, 1, 0]
中间柱子： []
目标柱子： []
移动后的汉诺塔为：
原柱子： []
中间柱子： []
目标柱子： [2, 1, 0]
3、KMP 算法（字符串匹配问题）
（1）字符串匹配问题
现有一个目标字符串 A，一个待匹配字符串（模式串） B，如何判断 A 中是否存在 B 字符串？
一般方法有两种：
暴力匹配：一个一个字符进行匹配。
KMP 算法：改进的字符串匹配。核心是 跳过无用匹配，减少匹配次数。
（2）暴力匹配
【思路：】
假设当前目标字符串 A 已经匹配到了 i 位置，待匹配字符串 B 已匹配到了 j 位置。
则
如果字符匹配成功，即 A[i] == B[j]，则进行下一个字符匹配，即 i++，j++。
如果字符匹配失败，即 A[i] != B[j]，则进行回溯，回到 A 开始匹配字符，并对下一个字符重新进行匹配，即 i = i - j + 1, j = 0。
注：
使用暴力匹配可能会 执行大量的回溯过程，造成时间的浪费。
时间复杂度为 O(n*m)，n 为目标字符串长度，m 为模式串长度。 【举例：】
现有目标字符串 ABDABC，待匹配字符串为 ABC。
第一次匹配：
ABDABC
ABC
匹配失败。 第二次匹配：
ABDABC
ABC
匹配失败。 第三次匹配：
ABDABC
ABC
匹配失败。 同理挨个字符向后匹配。 【代码实现：】
package com.lyh.algorithm; /**
* 字符串匹配
*/
public class StringMatch {
public static void main(String[] args) {
String target = "BBC ABCDAB ABCDABCDABDE";
String current = "ABCDABD";
System.out.println("直接调用 String 的 contains 方法结果为： " + contains(target, current));
System.out.println("暴力匹配，子字符串第一次出现的下标为： " + forceMatch(target, current));
} /**
* 暴力匹配
* @param a 目标字符串
* @param b 待匹配字符串
* @return 匹配失败返回 -1，否则返回第一次出现的下标
*/
public static int forceMatch(String a, String b) {
char[] target = a.toCharArray(); // 将 目标字符串 转为 字符数组
char[] current = b.toCharArray(); // 将 待匹配字符串 转为 字符数组 // i 用于记录 目标字符串 当前匹配的下标，j 用于记录 待匹配字符串 当前匹配的下标
int i = 0, j = 0;
// 挨个字符进行匹配
while (i < target.length && j < current.length) {
// 匹配成功，则匹配下一个字符
if (target[i] == current[j]) {
i++;
j++;
} else {
// 匹配失败，回退到开始字符的下一个位置重新进行匹配
i = i - j + 1;
j = 0;
}
} // 当 j 为待匹配字符串长度时，匹配成功
if (j == current.length) {
return i - j;
}
return -1;
} /**
* 一个取巧的方法，直接调用 String 的 contains 方法进行匹配（无法返回第一次出现的位置）
* @param target 目标字符串
* @param current 待匹配字符串
* @return 匹配成功返回 true
*/
public static boolean contains(String target, String current) {
return target.contains(current);
}
} 【输出结果：】
直接调用 String 的 contains 方法结果为： true
暴力匹配，子字符串第一次出现的下标为： 15
（3）KMP 算法
KMP 指的是 Knuth-Morris-Pratt，三个人名拼接而成，用于在一个文本串 S 中 查找一个模式串 P 出现的位置。
暴力匹配 是 挨个匹配 字符，而 KMP 是利用现有模式串信息，跳过一些无用的匹配操作，省去大量回溯时间。即暴力匹配过程中，若匹配失败，主串会发生回溯。而 KMP 算法匹配失败，主串不发生回溯，移动模式串去匹配。
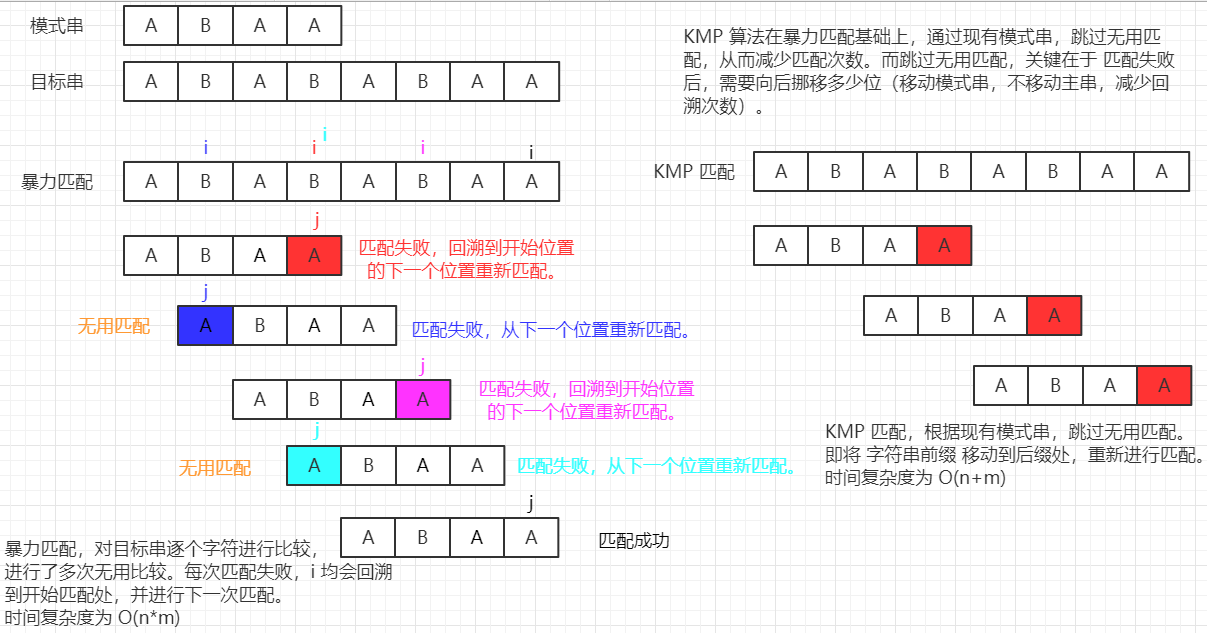
【KMP 核心：】
KMP 核心是通过 现有的模式串，跳过无用的匹配，减少回溯次数，从而提高匹配效率。
KMP 算法为了减少无用匹配，根据模式串前后缀关系，将模式串从前缀位置移动到与其相同的后缀位置，从而跳过一些无用匹配。
并根据前后缀关系，得到一个 next 数组，用于记录模式串下标 i 匹配失败后，应该从 next[i] 处与当前主串重新开始比较。
next[i] 存储的是前 i 个字符（即 0 ~ i - 1）组成的字符串中 最大相等前后缀的长度值。
相当于将模式串向后移动 i - next[i] 个位置（使前缀移动到后缀处），并与主串进行比较。 【推导过程：】
如何减少无用匹配（以主串：ABABABAA，模式串：ABAA 为例）：
第一次匹配时：
ABABABAA
ABAA
发现 ABAB ABAA 前三个字符是一致的（ABA），
暴力匹配时，主串会回溯到开始字符的下一个位置进行比较，如下：
ABABABAA
ABAA
此时不匹配，继续匹配
ABABABAA
ABAA
可以发现，又出现了 ABAB ABAA 的情况，如果继续暴力处理，那么会多出很多无用操作。
那么能否根据现有的 模式串，作出一些处理，从而跳过一些无用的操作呢？ 这里先介绍一下 字符串前缀、后缀（以字符串 ABAA 为例）：
前缀：{A, AB, ABA}，含头不含尾的子字符串。
后缀：{BAA, AA, A}，含尾不含头的子字符串。 通过观察 ABAB ABAA 前三个字符 ABA，可以发现
ABA 前缀为 {A, AB}，后缀为 {BA, A}，其最大公共串为 {A}，
而在暴力匹配时可以发现 ABA 的相同前缀、后缀 中间的匹配操作 均为无用操作。
即下面匹配操作是无用操作，可以直接跳过。
ABABABAA
ABAA
即可以直接将 模式串 从前缀处 移动到 相同后缀处，并重新开始比较（划重点）。 那么能否 根据 模式串的 前、后缀 总结出一个规律呢？（以 ABAA 为例）
将 ABAA 按照位置关系视为 0 ~ 3 位（此处使用），当然也可以视为 1 ~ 4 位。
即
0 1 2 3 或者 0 1 2 3 4
A B A A A B A A 进行匹配时，若模式串第 0 位就匹配失败，则模式串移动到 当前主串位置的下一个位置开始匹配：
即
主串： C B A A A
模式串： A B A A
模式串第 0 位匹配失败后，下一次匹配时 模式串的第 0 位 从当前主串位置的下一个位置开始（当前主串位置下标为 0）：
主串： C B A A A
模式串： A B A A 进行匹配时，若模式串第 1 位匹配失败，且此时模式串 第 0 位（A）没有 前缀、后缀，则模式串移动到 当前主串位置开始匹配。
即
主串： A C A A A
模式串： A B A A
模式串第 1 位匹配失败后，下一次匹配时 模式串的第 0 位 从当前主串位置开始（当前主串下标为 1）比较。
主串： A C A A A
模式串： A B A A 进行匹配时，若模式串第 2 位匹配失败，其此时模式串 第 0 ~ 1 位（AB）的 前缀、后缀 中没有最大公共串，则模式串移动到 当前主串位置开始匹配。
即
主串： A B C A A
模式串：A B A A
模式串第 2 位匹配失败后，下一次匹配时 模式串的第 0 位 从当前主串位置开始（当前主串下标为 2）比较。
主串： A B C A A
模式串： A B A A 进行匹配时，若模式串第 3 位匹配失败，其此时模式串 第 0 ~ 2 位（ABA）的前缀、后缀 最大公共串为 1（A），则模式串移动到 当前主串位置开始匹配。
即
主串： A B A C A
模式串： A B A A
模式串第 3 位匹配失败后，下一次匹配时 模式串的第 1 位 从当前主串位置开始（当前主串下标为 3）比较。
主串： A B A C A
模式串： A B A A 通过上面对模式串 ABAA 的分析，
当模式串第 0 位匹配失败时，模式串需要移动 1 位，且主串需要向后移动 1 位。使得模式串下一次第 0 位 与 主串当前位置下一个位置开始比较，记此时为 -1。
当模式串第 1 位匹配失败时，模式串前 0 位没有最大公共前、后缀串，此时模式串向后移动 1 位，主串不移动。使得模式串下一次第 0 位 与 主串当前位置开始比较，记此时为 0。
当模式串第 2 位匹配失败时，模式串前 1 位没有最大公共前、后缀串，此时模式串向后移动 2 位，主串不移动。使得模式串下一次第 0 位 与 主串当前位置开始比较，记此时为 0。
当模式串第 3 位匹配失败时，模式串前 2 位存在最大公共串且长度为 1，此时模式串向后移动 2 位，主串不移动。使得模式串下一次第 1 位 与 主串当前位置开始比较，记此时为 1。
可以得到一个规律，
模式串第 i 为匹配失败时，模式串下一次匹配从 第 j 位开始与主串比较。
第 j 位指的是 模式串 第 0 ~ i-1 串的 最大前、后缀长度。
而模式串需要移动的位数则为： i - j，即将模式串前缀 移动到 最长公共 后缀处。 也即 KMP 中的 next 数组（不同人定义的 next 可能有些许区别，但大体操作类似），
next 数组元素表示 当前模式串下标 匹配失败后，下一次模式串中 需要与 主串进行匹配的 下标位置（即最长公共前、后缀的前缀的下一个位置）。
而模式串需要移动的位数则为： i - next[i]。 所以可以得到 ABAA 的 next 数组如下：
0 1 2 3
模式串： A B A A
next数组： -1 0 0 1
移动位数： 1 1 2 2 如果将 ABAA 视为 1~4 位，则每次加 1 即可，即 第 j 位指的是 模式串 第 0 ~ i-1 串的 最大前、后缀长度 加 1。
0 1 2 3 4
模式串： A B A A
next数组： 0 1 1 2
移动位数： 1 1 2 2
（4）KMP 算法的 next 数组代码实现（模式串自匹配）
【如何使用代码实现 KMP 的 next 数组：】
通过上面分析， next 数组的求解是 KMP 关键之一，那么如何求解呢？
注意，此处的 next 每个元素表示的是 模式串当前元素下标 与 主串 匹配失败后，下一次 模式串 开始匹配的下标值。
即 next[j] 表示 模式串下标为 j 的元素 与 主串匹配失败后，下一次模式串 开始匹配的下标位置（即 0 ~ j-1 表示的 字符串中 最长公共前、后缀的 前缀的下一个位置，也即最长前后缀长度）。
可参考上述推导过程推理 next 的计算。 假设现在模式串 str 长度为 n, i 表示当前模式串下标（0 ~ n-1），j 表示最大前缀的下一个位置的下标。
由于模式串第 0 位前面没有字符，此处设定为 next[0] = -1。
而模式串第 1 位前面有一个字符，但是没有前、后缀，此处设定为 next[1]= 0。
所以 模式串只需从第 2 位开始计算。记初始 i = 2, j = 0。（i 永远比 j 大） 强调一下：
此处 next[i] 指的是 前 i 个字符（即 0 ~ i - 1 所表示的字符串）中最大相等前后缀长度。
i - 1 表示当前最大相等后缀的下一个位置，j 表示当前最大相等前缀的下一个位置。
也就是说前 j 个（0 ~ j-1）字符是当前最大的相等前缀。
而 下标为 j 与 i - 1 所在字符 分别表示下一次需要比较的前缀 与 后缀，即比较 str[j] 与 str[i - 1] 是否相等即可。
若 str[j] == str[i - 1]，那么最大相等前后缀长度又可以增加一位，此时 j++，i++。
若 str[j] != str[i - 1]，则说明当前 0 ~ j 所表示的前缀 与 (i - j - 1) ~ (i - 1) 所表示的后缀不匹配，则需要从 0 ~ (j - 1) 所表示的前缀中 查找最大的前后缀 重新与 (i - j ) ~ (i - 1) 所表示的后缀匹配。
而 0 ~ (j - 1) 中最大前后缀长度即 next[j] 的值，所以此时 j = next[j]。若 j 仍然不匹配，则继续调用 j = next[j] 进行回退，直至 j 退回到模式串第 0 个位置。 注：
由于 next[0] 不存在前 0 位字符串，所以定义其为 -1，表示当前模式串第 0 位与主串当前位置下一位开始比较。
i 如果从 1 开始定义，则 j 初始值可以设置为 -1。i 为 1 时，下标为 0 的字符为待匹配的后缀，但是不存在前缀，可以假定前面有一位待匹配的前缀，假定下标为 -1。
i 如果从 2 开始定义，则 j 初始值可以设置为 0。i 为 2 时，下标为 1 的字符为待匹配的后缀，下标为 0 为待匹配的前缀。 【代码实现为：（next 数组第一种写法）】
/**
* next 数组第一种写法。
* KMP 实质上是根据字符串前后缀的特点，将前缀字符移动到后缀位置，经过一系列推导根据 最大相等前后缀长度 得到一个 next 数组。
*
* next 数组存储的是 当前模式串匹配失败后，下一次与主串匹配的模式串的下标值（也可以理解为 模式串根据前后缀关系需要移动的位置）。
* 即 next[j] 表示的是 模式串中下标为 j 的元素与主串匹配失败后，下一次从 模式串中下标为 next[j] 的元素开始与 主串匹配。
* 也即相当于将 模式串移动 j - next[j] 个位置，然后重新与主串进行匹配。
* 而 next[j] 实际存储的 模式串 前 j 个字符 最大的相等的 前后缀的长度。
*
* 比如：
* 模式串为 ABAA
* 则其 next[3] 存储的是 ABA 的最大相等前后缀的长度。即 next[3] = 1.
*
* 注（以 ABAA 为例）：
* 字符串前缀为其 含头不含尾的 子字符串。比如：ABA 前缀为 {A, AB}.
* 字符串后缀为其 含尾不含头的 子字符串。比如：ABA 前缀为 {BA, A}.
* 记 next[0] = -1。next[1] = 0，均表示模式串向后挪一个位置（j - next[j]）。
* next[0] 表示前 0 位字符串（不存在），记为 -1.
* next[1] 表示前 1 位字符串（即 A 没有前后缀），记为 0.
* next[2] 表示前 2 位字符串（即 AB，没有最大相等的前后缀），记为 0.
* next[3] 表示前 3 位字符串（即 ABA，最大相等前后缀为 A，长度为 1），记为 1.
*
* @param pattern 模式串
* @return next 数组
*/
private static int[] getNext(String pattern) {
// 用于保存 next 数组
int[] next = new int[pattern.length()];
// 规定模式串第 0 位匹配失败后，下一次模式串第 0 位与 主串当前位置下一个位置 进行匹配，记此时为 -1
next[0] = -1;
// 模式串第 1 位匹配失败后，下一次模式串第 0 位与 主串当前位置进行匹配，记此时为 0
next[1] = 0;
// 遍历模式串，依次得到 模式串 第 i 位匹配失败后，下一次模式串需要从第 next[i] 位开始与主串进行匹配
// i 表示模式串当前下标，j 表示模式串最大相等前后缀的 前缀的下一个位置的下标
// i >= 2 时，模式串前 2 个字符才存在 前后缀，此时 next 求解才有意义
for (int i = 2, j = 0; i < pattern.length(); i++) {
// 模式串自匹配，为了求解 next[i]，需在模式串前 i 个元素中找到 最大前后缀
// j 表示的是当前最大前缀的下标，i-1 表示的是最大后缀的下标，若两者所在字符不匹配，则需要找到更小的前缀进行匹配，也即 j 需要回退
// 而 j 所在下标表示 0 ~ j-1 之前属于最长前缀，现在需要从 0~j-1 中找到新的最长前缀，而 next[j] 保存的正好是该值。
// 所以在此推出 j = next[j]
while(j > 0 && pattern.charAt(i - 1) != pattern.charAt(j)) {
j = next[j];
}
// 如果匹配，则说明当前最大前缀又可以增加一位，j 表示最长前缀的下一个位置（也即前缀长度），即 j++
if (pattern.charAt(i - 1) == pattern.charAt(j)) {
j++;
}
// 保存模式串下标为 i 匹配失败后，下一次从模式串开始匹配的下标位置
next[i] = j;
}
return next;
} 【举例：】
A B C D A B C E F
next[0] = -1,
next[1] = 1.
i = 2 时，j = 0，此时 str[i - 1] != str[j]，即 next[2] = 0.
i = 3 时，j = 0，此时 str[i - 1] != str[j]，即 next[3] = 0.
i = 4 时，j = 0，此时 str[i - 1] != str[j]，即 next[4] = 0.
i = 5 时，j = 0，此时 str[i - 1] == str[j]，则 j++，即 next[5] = 1.
i = 6 时，j = 1，此时 str[i - 1] == str[j]，则 j++，即 next[6] = 2.
i = 7 时，j = 2，此时 str[i - 1] == str[j]，则 j++，即 next[7] = 3.
i = 8 时，j = 3，此时 str[i - 1] != str[j]，则 j = next[j] = 0 即 next[8] = 0. 【代码实现为：（next 数组第二种写法）】
/**
* next 数组第二种写法。
* 上面第一种解法是 每次计算 前 i 个字符（i 从 2 开始， j 从 0 开始）的模式串的最大相等前后缀，并将最大前缀下标的下一个位置赋值给 next[i]。
* 而第二种解法是，每次计算 前 i + 1 个字符（i 从 1 开始，j 从 -1 开始）的模式串的最大相等前后缀，并将其值赋值给 next[i+1]。
* 虽然写法稍有不同，但是原理都是类似的。
* @param pattern 模式串
* @return next 数组
*/
private static int[] getNext2(String pattern) {
// 用于保存 next 数组
int[] next = new int[pattern.length()];
// 规定模式串第 0 位匹配失败后，下一次模式串第 0 位与 主串当前位置下一个位置 进行匹配，记此时为 -1
next[0] = -1;
// i 表示模式串下标， j 表示最长前缀下一个位置的下标
int i = 0, j = -1;
// 遍历求解 next 数组
while(i < pattern.length() - 1) {
// 计算出模式串以当前下标为后缀的 最大相等前后缀长度，并将其值赋给 下一个 next。
// 也即相当于 next[i] 保存的时 前 i 个字符（0 ~ i-1） 的最大前后缀长度
if (j == -1 || pattern.charAt(i) == pattern.charAt(j)) {
next[++i] = ++j;
} else {
j = next[j];
}
}
return next;
}
（5）改进的 KMP 算法（改进 next 数组求解）
【改进的 next 数组求解：】
next 数组求解优化，即改进的 KMP 算法，
与 第二个求解 next 数组方式类似，区别在于 j 回退位置。 比如：
主串 ABACABAA
模式串 ABAB
由于模式串最后一个字符匹配失败，按照之前的 next 数组求法，得到 ABAA 的 next 数组为 [-1, 0, 0, 1]。
则此时下一次匹配如下：
主串 ABACABAA
模式串 ABAB
可以很明显的看到此时的匹配无效，与上次匹配失败的字符相同。
此时应该直接一步到位，省去这次无用匹配。也即 模式串下标为 j 的字符回退时 若遇到相同的 字符，应该继续回退。
即第一次匹配失败后，直接进行如下匹配：
主串 ABACABAA
模式串 ABAB 即 模式串下标为 j 与 next[j] 字符相同时，应该继续求解 next[next[j]] 的值。
比如：
模式串： ABAB，可以得到 next 数组为 [-1, 0, 0, 1]
下标为 0 匹配失败时，初值为 -1,固定不变。
下标为 1 匹配失败时，下标为 1 的字符为 B、下标为 next[1] 的字符为 A，字符并不同，所以 next[1] = 0，与原 next 求解相同。
下标为 2 匹配失败时，下标为 2 的字符为 A、下标为 next[2] 的字符为 A，字符相同，所以 next[2] = next[next[2]] = next[0] = -1.
下标为 3 匹配失败时，下标为 3 的字符为 B，下标为 next[3] 的字符为 B，字符相同，所以 next[3] = next[next[3]] = next[1] = 0.
即改进后的 ABAB 得到的 next 数组为 [-1, 0, -1, 0]。 此时再次匹配：
主串 ABACABAA
模式串 ABAB
则下一次匹配为（跳过了无用的匹配）：
主串 ABACABAA
模式串 ABAB 【代码实现：】
/**
* next 数组求解优化，即改进的 KMP 算法，
* 与 第二个求解 next 数组方式类似，区别在于 j 回退位置。
* 比如：
* 主串 ABACABAA
* 模式串 ABAB
* 由于模式串最后一个字符匹配失败，按照之前的 next 数组求法，得到 ABAA 的 next 数组为 [-1, 0, 0, 1]。
* 则此时下一次匹配如下：
* 主串 ABACABAA
* 模式串 ABAB
* 可以很明显的看到此时的匹配无效，与上次匹配失败的字符相同。
* 此时应该直接一步到位，省去这次无用匹配。也即 模式串下标为 j 的字符回退时 若遇到相同的 字符，应该继续回退。
*
* 即 模式串下标为 j 与 next[j] 字符相同时，应该继续求解 next[next[j]] 的值。
* 比如：
* 模式串： ABAB，可以得到 next 数组为 [-1, 0, 0, 1]
* 下标为 0 匹配失败时，初值为 -1,固定不变。
* 下标为 1 匹配失败时，下标为 1 的字符为 B、下标为 next[1] 的字符为 A，字符并不同，所以 next[1] = 0，与原 next 求解相同。
* 下标为 2 匹配失败时，下标为 2 的字符为 A、下标为 next[2] 的字符为 A，字符相同，所以 next[2] = next[next[2]] = next[0] = -1.
* 下标为 3 匹配失败时，下标为 3 的字符为 B，下标为 next[3] 的字符为 B，字符相同，所以 next[3] = next[next[3]] = next[1] = 0.
* 即改进后的 ABAB 得到的 next 数组为 [-1, 0, -1, 0]。
*
* 此时再次匹配：
* 主串 ABACABAA
* 模式串 ABAB
* 则下一次匹配为（跳过了无用的匹配）：
* 主串 ABACABAA
* 模式串 ABAB
*
* @param pattern 模式串
* @return next 数组
*/
private static int[] getNext3(String pattern) {
int[] next = new int[pattern.length()];
next[0] = -1;
int i = 0, j = -1;
while(i < pattern.length() - 1) {
if (j == -1 || pattern.charAt(i) == pattern.charAt(j)) {
// next[++i] = ++j;
if (pattern.charAt(++i) == pattern.charAt(++j)) {
next[i] = next[j];
} else {
next[i] = j;
}
} else {
j = next[j];
}
}
return next;
}
（6）完整的 KMP 算法如下：
包括两种求解 next 数组的方式，以及 next 数组优化后的方式，以及 kmp 根据 next 数组进行匹配。
【代码实现：】
package com.lyh.algorithm; import java.util.Arrays; /**
* 字符串匹配
*/
public class StringMatch2 {
public static void main(String[] args) {
String target = "BBC ABCDAB ABCDABCDABDE";
String pattern = "ABCDABD";
System.out.println(Arrays.toString(getNext("ABAB")));
System.out.println(Arrays.toString(getNext("ABCDABCEF"))); System.out.println(Arrays.toString(getNext2("ABAB")));
System.out.println(Arrays.toString(getNext2("ABCDABCDEF"))); System.out.println(Arrays.toString(getNext3("ABAB")));
System.out.println(Arrays.toString(getNext3("ABCDABCDEF")));
System.out.println(kmp(target, pattern));
} /**
* KMP 算法，根据模式串生成 next 数组，减少无用匹配次数。
* @param target 主串
* @param pattern 模式串
* @return 匹配失败返回 -1，否则返回相应的下标
*/
public static int kmp(String target, String pattern) {
// 获取 next 数组，用于模式串匹配失败后，下一次与主串匹配的位置。
int[] next = getNext(pattern);
int i = 0, j = 0;
// 开始匹配
// i 表示主串所处下标，j 表示模式串所处下标（j 同时也表示的是最长前缀的下一个位置）
while (i < target.length() && j < pattern.length()) {
// j == -1 表示下一次模式串 第 -1 位 与 当前主串位置进行比较，也即下一次 为模式串第 0 位 与 当前主串位置下一位置进行比较， 所以 i++,j++
// target.charAt(i) == pattern.charAt(j) 表示模式串下标为 j 的字符与 主串匹配，也即当前 模式串 0~j 均可以作为最长前缀。
// 也即下一次 模式串从下标为 j + 1 处 与 主串下一个位置开始比较，所以 i++,j++。
if (j == -1 || target.charAt(i) == pattern.charAt(j)) {
i++;
j++;
} else {
// 此时属于 target.charAt(i) != pattern.charAt(j) 的情况，模式串需要进行回退。
// next[j] 表示的是模式串下标为 j 的字符匹配失败后，下一次模式串中 应该与 主串当前位置进行 匹配的字符下标
j = next[j];
}
}
// 匹配成功
if (j == pattern.length()) {
return i - j;
}
// 匹配失败
return -1;
} /**
* next 数组第一种写法。
* KMP 实质上是根据字符串前后缀的特点，将前缀字符移动到后缀位置，经过一系列推导根据 最大相等前后缀长度 得到一个 next 数组。
*
* next 数组存储的是 当前模式串匹配失败后，下一次与主串匹配的模式串的下标值（也可以理解为 模式串根据前后缀关系需要移动的位置）。
* 即 next[j] 表示的是 模式串中下标为 j 的元素与主串匹配失败后，下一次从 模式串中下标为 next[j] 的元素开始与 主串匹配。
* 也即相当于将 模式串移动 j - next[j] 个位置，然后重新与主串进行匹配。
* 而 next[j] 实际存储的 模式串 前 j 个字符 最大的相等的 前后缀的长度。
*
* 比如：
* 模式串为 ABAA
* 则其 next[3] 存储的是 ABA 的最大相等前后缀的长度。即 next[3] = 1.
*
* 注（以 ABAA 为例）：
* 字符串前缀为其 含头不含尾的 子字符串。比如：ABA 前缀为 {A, AB}.
* 字符串后缀为其 含尾不含头的 子字符串。比如：ABA 前缀为 {BA, A}.
* 记 next[0] = -1。next[1] = 0，均表示模式串向后挪一个位置（j - next[j]）。
* next[0] 表示前 0 位字符串（不存在），记为 -1.
* next[1] 表示前 1 位字符串（即 A 没有前后缀），记为 0.
* next[2] 表示前 2 位字符串（即 AB，没有最大相等的前后缀），记为 0.
* next[3] 表示前 3 位字符串（即 ABA，最大相等前后缀为 A，长度为 1），记为 1.
*
* @param pattern 模式串
* @return next 数组
*/
private static int[] getNext(String pattern) {
// 用于保存 next 数组
int[] next = new int[pattern.length()];
// 规定模式串第 0 位匹配失败后，下一次模式串第 0 位与 主串当前位置下一个位置 进行匹配，记此时为 -1
next[0] = -1;
// 模式串第 1 位匹配失败后，下一次模式串第 0 位与 主串当前位置进行匹配，记此时为 0
next[1] = 0;
// 遍历模式串，依次得到 模式串 第 i 位匹配失败后，下一次模式串需要从第 next[i] 位开始与主串进行匹配
// i 表示模式串当前下标，j 表示模式串最大相等前后缀的 前缀的下一个位置的下标
// i >= 2 时，模式串前 2 个字符才存在 前后缀，此时 next 求解才有意义
for (int i = 2, j = 0; i < pattern.length(); i++) {
// 模式串自匹配，为了求解 next[i]，需在模式串前 i 个元素中找到 最大前后缀
// j 表示的是当前最大前缀的下标，i-1 表示的是最大后缀的下标，若两者所在字符不匹配，则需要找到更小的前缀进行匹配，也即 j 需要回退
// 而 j 所在下标表示 0 ~ j-1 之前属于最长前缀，现在需要从 0~j-1 中找到新的最长前缀，而 next[j] 保存的正好是该值。
// 所以在此推出 j = next[j]
while(j > 0 && pattern.charAt(i - 1) != pattern.charAt(j)) {
j = next[j];
}
// 如果匹配，则说明当前最大前缀又可以增加一位，j 表示最长前缀的下一个位置（也即前缀长度），即 j++
if (pattern.charAt(i - 1) == pattern.charAt(j)) {
j++;
}
// 保存模式串下标为 i 匹配失败后，下一次从模式串开始匹配的下标位置
next[i] = j;
}
return next;
} /**
* next 数组第二种写法。
* 上面第一种解法是 每次计算 前 i 个字符（i 从 2 开始， j 从 0 开始）的模式串的最大相等前后缀，并将最大前缀下标的下一个位置赋值给 next[i]。
* 而第二种解法是，每次计算 前 i + 1 个字符（i 从 1 开始，j 从 -1 开始）的模式串的最大相等前后缀，并将其值赋值给 next[i+1]。
* 虽然写法稍有不同，但是原理都是类似的。
* @param pattern 模式串
* @return next 数组
*/
private static int[] getNext2(String pattern) {
// 用于保存 next 数组
int[] next = new int[pattern.length()];
// 规定模式串第 0 位匹配失败后，下一次模式串第 0 位与 主串当前位置下一个位置 进行匹配，记此时为 -1
next[0] = -1;
// i 表示模式串下标， j 表示最长前缀下一个位置的下标
int i = 0, j = -1;
// 遍历求解 next 数组
while(i < pattern.length() - 1) {
// 计算出模式串以当前下标为后缀的 最大相等前后缀长度，并将其值赋给 下一个 next。
// 也即相当于 next[i] 保存的时 前 i 个字符（0 ~ i-1） 的最大前后缀长度
if (j == -1 || pattern.charAt(i) == pattern.charAt(j)) {
next[++i] = ++j;
} else {
j = next[j];
}
}
return next;
} /**
* next 数组求解优化，即改进的 KMP 算法，
* 与 第二个求解 next 数组方式类似，区别在于 j 回退位置。
* 比如：
* 主串 ABACABAA
* 模式串 ABAB
* 由于模式串最后一个字符匹配失败，按照之前的 next 数组求法，得到 ABAA 的 next 数组为 [-1, 0, 0, 1]。
* 则此时下一次匹配如下：
* 主串 ABACABAA
* 模式串 ABAB
* 可以很明显的看到此时的匹配无效，与上次匹配失败的字符相同。
* 此时应该直接一步到位，省去这次无用匹配。也即 模式串下标为 j 的字符回退时 若遇到相同的 字符，应该继续回退。
*
* 即 模式串下标为 j 与 next[j] 字符相同时，应该继续求解 next[next[j]] 的值。
* 比如：
* 模式串： ABAB，可以得到 next 数组为 [-1, 0, 0, 1]
* 下标为 0 匹配失败时，初值为 -1,固定不变。
* 下标为 1 匹配失败时，下标为 1 的字符为 B、下标为 next[1] 的字符为 A，字符并不同，所以 next[1] = 0，与原 next 求解相同。
* 下标为 2 匹配失败时，下标为 2 的字符为 A、下标为 next[2] 的字符为 A，字符相同，所以 next[2] = next[next[2]] = next[0] = -1.
* 下标为 3 匹配失败时，下标为 3 的字符为 B，下标为 next[3] 的字符为 B，字符相同，所以 next[3] = next[next[3]] = next[1] = 0.
* 即改进后的 ABAB 得到的 next 数组为 [-1, 0, -1, 0]。
*
* 此时再次匹配：
* 主串 ABACABAA
* 模式串 ABAB
* 则下一次匹配为（跳过了无用的匹配）：
* 主串 ABACABAA
* 模式串 ABAB
*
* @param pattern 模式串
* @return next 数组
*/
private static int[] getNext3(String pattern) {
int[] next = new int[pattern.length()];
next[0] = -1;
int i = 0, j = -1;
while(i < pattern.length() - 1) {
if (j == -1 || pattern.charAt(i) == pattern.charAt(j)) {
// next[++i] = ++j;
if (pattern.charAt(++i) == pattern.charAt(++j)) {
next[i] = next[j];
} else {
next[i] = j;
}
} else {
j = next[j];
}
}
return next;
}
} 【输出结果：】
[-1, 0, 0, 1]
[-1, 0, 0, 0, 0, 1, 2, 3, 0]
[-1, 0, 0, 1]
[-1, 0, 0, 0, 0, 1, 2, 3, 4, 0]
[-1, 0, -1, 0]
[-1, 0, 0, 0, -1, 0, 0, 0, 4, 0]
15
4、贪心算法（集合覆盖问题）
（1）贪心算法
贪心算法 指的是 在对问题求解时，可以将问题简化成 若干类似的小问题，其每次解决小问题 的方式均是 当前情况下的最优选择（即 局部最优），最终得到原问题的最优解。
注：
贪心算法其虽然每一步都能保证最优解，但是其最终结果并不一定是最优的（接近最优解的结果）。
（2）集合覆盖问题
【问题：】
现有 K1 - K5 五辆公交车，其能经过的站台（A - H）如下所示：
公交车 站台
K1 "A", "B", "C"
K2 "D", "A", "E"
K3 "F", "B", "G"
K4 "B", "C"
K5 "G", "H"
如何选择最少的 公交车，能经过所有的公交站台。 【思路：】
穷举法 不切实际，肯定不能采取。
可以使用贪心算法，每次选择 当前覆盖最多公交站 的公交，可以快速选择到所有公交站台。
贪心法步骤：
Step1：首先获取到所有的公交站台信息 allStation。
Step2：遍历所有公交车，根据公交车 站台信息 与 allStation 比较，从中找到一个 覆盖最多公交站 的公交。
记录此时的公交车，并将当前公交车经过的 站台 从 allStation 中去除。
Step3：重复 Step2，直至 allStation 为空，也即经过所有公交站台 最少公交车 已经找到。 【举例分析：】
Step1：首先获取到所有公交站台信息，allStation = ["A", "B", "C", "D", "E", "F", "G", "H"];
Step2：遍历 K1 - K5 公交车，发现 K1、K2、K3 均能覆盖 3 个站台，K4、K5 能覆盖 2 个站台。
按照顺序，先记录 K1 公交车，并去除 allStation 中相应的站台，此时 allStation = ["D", "E", "F", "G", "H"];
Step3：再次遍历 K1 - K5（跳过 K1 亦可），此时 K2、K3、K5 能覆盖 2 个站台，K1、K4 能覆盖 1 个站台。
按照顺序，先记录 K2 公交车，并去除 allStation 中相应的站台，此时 allStation = ["F", "G", "H"];
Step4：再次遍历 K1 - K5，此时 K3、K5 能覆盖 2 个站台，K1、K2、K4 能覆盖 1 个站台。
按照顺序，先记录 K3 公交车，并去除 allStation 中相应的站台，此时 allStation = ["H"];
Step5：再次遍历 K1 - K5，此时 K5 能覆盖 1 个站台，K1 - K4 能覆盖 0 个站台。
记录 K5，并去除 allStation 中相应的站台，此时 allStation = [];
Step6：allStation 为空，即所有公交站台均可访问，此时公交为 [K1, K2, K3, K5] 注：
若第一次选择的并非 K1，而是 K2，则可能的结果为：[K2, k3, K5, K4].
可以发现，可能存在多个解，即 贪心法得到的结果不一定是最优解，但一定近似最优解。 【代码实现：】
package com.lyh.algorithm; import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
import java.util.List; public class Greedy {
public static void main(String[] args) {
greedy();
} /**
* 贪心算法求解 集合覆盖问题。
* 每次选取当前情况下的最优解，从而最终得到结果（结果不一定为最优解，但是近似最优解）
*/
public static void greedy() {
// 设置公交经过的站台
HashSet<String> k1 = new HashSet<>();
k1.add("A");
k1.add("B");
k1.add("C"); HashSet<String> k2 = new HashSet<>();
k2.add("D");
k2.add("A");
k2.add("E"); HashSet<String> k3 = new HashSet<>();
k3.add("F");
k3.add("B");
k3.add("G"); HashSet<String> k4 = new HashSet<>();
k4.add("B");
k4.add("C"); HashSet<String> k5 = new HashSet<>();
k5.add("G");
k5.add("H"); // 保存所有公交 以及 公交站台信息
HashMap<String, HashSet<String>> bus = new HashMap<>();
bus.put("K1", k1);
bus.put("K2", k2);
bus.put("K3", k3);
bus.put("K4", k4);
bus.put("K5", k5); // 保存所有站台信息
HashSet<String> allStation = new HashSet<>();
for (String k : bus.keySet()) {
allStation.addAll(bus.get(k));
} // 用于记录最终结果
List<String> result = new ArrayList<>(); // 站台非空时，记录经过 最多 站台的 公交
while(!allStation.isEmpty()) {
// 用于记录经过 最多站台 的公交
String maxKey = null;
// 遍历各公交
for (String k : bus.keySet()) {
// 获取公交经过的站台信息
HashSet<String> temp = bus.get(k);
// 取当前 公交经过的 所有站台 与 总站台 的交集，并将交集 赋给 当前公交，用于记录当前公交所经过的最多站台数量
temp.retainAll(allStation);
// 用于记录当前场合下，经过 最多站台 的公交（局部最优）
if (maxKey == null || temp.size() > bus.get(maxKey).size()) {
maxKey = k;
}
}
if (maxKey != null) {
// 记录当前经过 最多站台的 公交
result.add(maxKey);
// 从所有公交站台中 移除 已经可以被经过的 公交站台
allStation.removeAll(bus.get(maxKey));
}
} System.out.println("经过所有站台所需最少公交为：" + result);
}
} 【输出结果：】
经过所有站台所需最少公交为：[K1, K2, K3, K5]
3、动态规划（0/1 背包问题）
（1）动态规划
动态规划（Dynamic Programming）核心思想与 分治算法类似，都是将 大问题划分为若干个小问题求解，从子问题的解中得到原问题的答案。
但不同之处在于 分治法 适用于 子问题相互独立的 情况，而动态规划 适用于 子问题不相互独立的情况，即 动态规划求解 建立在 上一个子问题的解的基础上。可以采用填表的方式，逐步推算得到最优解。
【动态规划关注点：】
最优子结构：每个阶段的状态可以从之前某个阶段直接得到。
状态转移：如何从一个状态 转移 到另一个状态。
注：
动态规划是以 空间 换 时间，其将每个子问题的计算结果保存，需要时直接取出，减少了重复计算子问题的时间。
（2）0/1 背包问题
【问题描述：】
背包问题是 给定一个容量的背包，以及若干个 具有一定 价值 以及 容量的物品，
在 保证 背包的容量下，选择物品放入背包，使得背包价值 最大。
注：
背包问题可以分为：0/1 背包、完全背包。
0/1 背包指的是 同一物品只能存在一个在背包中。
完全背包指的是 有多个相同的物品可以放入背包中。 【0/1 背包分析：】
假设有 n 个物品，背包重量为 m。
使用一维数组 weight[i] 表示 第 i 个物品的 重量。
使用一维数组 value[i] 表示 第 i 个物品的 价值。
使用二维数组 maxValue 用于记录物品放入背包的结果，maxValue[i][j] 表示前 i 个物品能装入容量为 j 的背包的最大价值，则 maxValue[n][m] 即为背包所能存放的最大价值。 对于 第 i-1 个物品，装入容量为 j 的背包，则其装入背包总价值为 maxValue[i-1][j]，
对于 第 i 个物品，
若其重量大于背包重量，即 weight[i] > j，则该物品肯定不能放入背包。此时背包最大价值仍为上一次的最大值，即 maxValue[i][j] = maxValue[i-1][j]。
若其重量小于等于背包重量，即 weight[i] <= j，则该物品可以放入背包。将物品放入背包，并重新计算当前最大价值。
物品放入背包，去除 当前物品容量时 背包的最大价值 并加上当前物品价值，即可得到当前物品存入背包后的最大价值，即 maxValue[i][j] = maxValue[i-1][j - weight[i]] + value[i]
计算原有价值以及 新价值的最大值作为当前背包最大价值（状态转移），即 Math.max(maxValue[i-1][j], maxValue[i-1][j-weight[i]] + value[i]))
注：
由于每次都将子问题解记录，所以可以避免重复计算子问题解。 若想输出放入背包的物品，可以根据 maxValue[i][j] 、maxValue[i-1][j] 反推。
maxValue[i][j] 大于 maxValue[i-1][j] 时，第 i 个物品肯定进入背包。 【举例：】
现有 3 个物品，价值为 {1500, 3000, 2000}，重量为 {1, 4, 3}。背包容量为 4.
则使用 二维数组 记录各容量背包下物品存放最大价值如下表：
1 2 3 4
0 0 0 0 0
1 0 1500 1500 1500 1500
2 0 1500 1500 1500 3000
3 0 1500 1500 2000 3500
注：
行表示物品，列表示背包容量。行列组合起来表示 某背包容量下 物品存放的最大价值。
比如：
第一行，存放第一个物品，重量为 1，在背包容量为 1~4 的情况下,均能存放，则其最大价值为 1500.
第二行，存放第二个物品，重量为 4，在背包容量为 1~3 的情况下，不能存放，则其最大价值为 1500（只能存放第一个物品），
但其在背包容量为 4 时可以存放，此时最大价值为 3000，且去除了第一个物品，只存放第二个物品。
第三行，存放第三个物品，重量为 3，在背包容量为 1~2 的情况下，不能存放，则其最大价值为 1500，
而其在背包容量为 3 时可以存放，此时最大价值为 2000，只存放第三个物品。
在背包容量为 4 时也可以存放，此时最大价值为 3500，存放第三个物品 和 第一个物品。 【代码实现：】
package com.lyh.algorithm; import java.util.ArrayList;
import java.util.List; /**
* 0/1 背包问题
*/
public class Knapsack {
public static void main(String[] args) {
int[] value = new int[]{1500, 3000, 2000}; // 设置物品价值
int[] weight = new int[]{1, 4, 3}; // 设置物品容量
int m = 4; // 设置背包容量
int n = value.length; // 设置物品总数量
knapsack(value, weight, n, m);
} /**
* 0/1 背包
* @param value 物品价值
* @param weight 物品重量
* @param count 物品总数
* @param capacity 背包总容量
*/
public static void knapsack(int[] value, int[] weight, int count, int capacity) {
// 背包存放最大价值,maxValue[i][j] 表示第 i 个物品存放在 容量为 j 的背包中的最大价值
// 其中第一行、第一列均为 0，便于计算。
int[][] maxValue = new int[count + 1][capacity + 1];
// 依次求解各个容量背包下物品存放的最大价值
// i 表示第 i 个物品，j 表示 容量为 j 的背包
for (int i = 1; i < count + 1; i++) {
for (int j = 1; j < capacity + 1; j++) {
// 若背包容量小于当前物品，则当前物品肯定不能存进背包，直接赋值上一个求解值即可
// 由于 i 从 1 开始计数，所以访问第一个物品重量时为 weight[i - 1],访问第一个物品价值为 value[i -1]，保证从下标为 0 开始访问。
if (j < weight[i - 1]) {
maxValue[i][j] = maxValue[i - 1][j];
} else {
// 背包容量 大于等于当前物品，则当前物品可以存入背包，则重新计算最大价值
// 当前物品存入背包价值为： 去除 当前物品容量时 背包的最大价值 与 当前物品价值 之和
int currentValue = maxValue[i - 1][j - weight[i - 1]] + value[i - 1];
// 计算当前物品价值 与 之前价值 最大值，并记录
maxValue[i][j] = Math.max(currentValue, maxValue[i - 1][j]);
}
}
} /**
* 遍历输出各个容量下 背包存放物品的价值
*/
System.out.println("各容量背包下，存放物品的最大值如下： ");
for (int i = 0; i < count + 1; i++) {
for (int j = 0; j < capacity + 1; j++) {
System.out.print(maxValue[i][j] + " ");
}
System.out.println();
} System.out.println("容量为： " + capacity + " 的背包存放最大物品价值为： " + maxValue[count][capacity]); // 反推出 存入 背包的物品
int j = capacity; // 记录背包容量
List<Integer> list = new ArrayList<>(); // 记录物品下标
for (int i = count; i > 0; i--) {
// maxValue[i][j] 大于 maxValue[i - 1][j]，则第 i 个物品肯定进入背包了
if (maxValue[i][j] > maxValue[i - 1][j]) {
list.add(i - 1); // 记录物品下标
j -= weight[i - 1]; // 查找去除当前物品下标后的背包存储的物品
}
if (j == 0) {
break; // 背包中物品都已取出
}
}
System.out.println("存入背包的物品为： ");
for (int i = 0; i < list.size(); i++) {
System.out.println("第 " + (list.get(i) + 1) + " 个物品，价值为： " + value[list.get(i)] + " ，重量为： " + weight[list.get(i)]);
}
}
} 【输出结果：】
各容量背包下，存放物品的最大值如下：
0 0 0 0 0
0 1500 1500 1500 1500
0 1500 1500 1500 3000
0 1500 1500 2000 3500
容量为： 4 的背包存放最大物品价值为： 3500
存入背包的物品为：
第 3 个物品，价值为： 2000 ，重量为： 3
第 1 个物品，价值为： 1500 ，重量为： 1
Java 内功修炼 之 数据结构与算法（二）的更多相关文章
- Java 内功修炼 之 数据结构与算法（一）
一.基本认识 1.数据结构与算法的关系? (1)数据结构(data structure): 数据结构指的是 数据与数据 之间的结构关系.比如:数组.队列.哈希.树 等结构. (2)算法: 算法指的是 ...
- 编程内功修炼之数据结构—BTree（二）实现BTree插入、查询、删除操作
1 package edu.algorithms.btree; import java.util.ArrayList; import java.util.List; /** * BTree类 * * ...
- Java数据结构和算法(二)--队列
上一篇文章写了栈的相关知识,而本文会讲一下队列 队列是一种特殊的线性表,在尾部插入(入队Enqueue),从头部删除(出队Dequeue),和栈的特性相反,存取数据特点是:FIFO Java中queu ...
- 学习JavaScript数据结构与算法 (二)
学习JavaScript数据结构与算法 的笔记 包含第四章队列, 第五章链表 本人所有文章首发在博客园: http://www.cnblogs.com/zhangrunhao/ 04队列 实现基本队列 ...
- Android版数据结构与算法(二):基于数组的实现ArrayList源码彻底分析
版权声明:本文出自汪磊的博客,未经作者允许禁止转载. 本片我们分析基础数组的实现--ArrayList,不会分析整个集合的继承体系,这不是本系列文章重点. 源码分析都是基于"安卓版" ...
- Java内功修炼系列一反射
“JAVA反射机制是在运行状态中,对于任意一个类,都能够知道这个类的所有属性和方法:对于任意一个对象,都能够调用它的任意方法和属性:这种动态获取信息以及动态调用对象方法的功能称为java语言的反射机制 ...
- javascript 数据结构与算法---二叉数
二叉树,首先了解一些关于二叉数的概念(来自百度百科) 1. 二叉树(Binary tree)是树形结构的一个重要类型 2. 定义: 二叉树(binary tree)是指树中节点的度不大于2的有序树,它 ...
- 编程内功修炼之数据结构—BTree（一）
BTree,和二叉查找树和红黑树中一样,与关键字相联系的数据作为关键字存放在同一节点上. 一颗BTree树具有如下的特性:(根为root[T]) 1)每个节点x有以下域: (a)n[x],当前存储在节 ...
- 编程内功修炼之数据结构—BTree（三）总结
BTree必须通过各种编程约束,使得不脱离BTree的本身特性: 1)BTree关键字插入操作:插入过程中,如果节点关键字达到上限,添加分裂约束,从而控制每个节点的关键字数维持在 t-1~2*t-1内 ...
随机推荐
- tensorflow Mobilenet 导出模型的方法
python export_inference_graph.py --input_type image_tensor --pipeline_config_path ssd_mobilenet_v1_c ...
- golang Gin framework with websocket
概述 golang websocket 库 示例 后端 前端 结论 概述 对于 golang 的 web 开发, 之前写过 2 篇 blog, 分别介绍了: 在 Gin 框架下, 各类 http AP ...
- PS文字
点文本 直接单击鼠标可输点文字 输完后在离文字较远的地方出现白色箭头单击可结束输入,也可选择其他图层结束输入 再次修改文字可双击文字缩览图 出现黑色小箭头可以在输入到的情况下拖动文字,文字工具下按Ct ...
- TCP/IP的十个问题
一.TCP/IP模型 TCP/IP协议模型(Transmission Control Protocol/Internet Protocol),包含了一系列构成互联网基础的网络协议,是Internet的 ...
- apache自带的ab测试失败请求原因
只要出现 Failed requests 就会多出现一行要求失败的各原因的数据统计,分别有 Connect, Length, 与 Exception 三种,分别代表的意义为:Connect ...
- Python之包的相关
包的产生: 由于模块不断更新,越写越大,仅用单个py文件会使模块逻辑不够清晰,所以需要将模块的不同功能放入不同的py文件,然后将所有py文件放在一个目录内,这个目录就是包 包就是一个包含用__init ...
- Python中while循环初识
基本结构 while 条件: 循环体 基本原理: 1.先判断条件是否为True 2.如果是True进入循环体 3.执行到循环体的底部 4.继续判断条件,条件为True,再次进入 ...
- 想买保时捷的运维李先生学Java性能之 JIT即时编译器
前言 本文记录日常学习<深入理解Java虚拟机>,不知道为啥感觉看一遍也就过了,喜欢动动手理解理解,这样才有点感觉,静不下心来的时候,看书抄书也可以用这个办法. 一.什么是JIT(Just ...
- Github上的沙雕项目，玩100遍都不够
这段时间大家在家自我隔离.居家办公憋坏了吧.为了打发这种无聊的生活,我决定拿出我在github上珍藏多年的沙雕项目,让大家在无聊的时候可以打发时间. Github作为互联网上最大的开源社区,一直备受程 ...
- java安全编码指南之:线程安全规则
目录 简介 注意线程安全方法的重写 构造函数中this的溢出 不要在类初始化的时候使用后台线程 简介 如果我们在多线程中引入了共享变量,那么我们就需要考虑一下多线程下线程安全的问题了.那么我们在编写代 ...