Test 1022

T1 AERODROM (二分答案

TimeLimit: 1000MS

Memory Limit: 32768KB

\(N\)个登机口，办理登机业务，第\(i\)个窗口的单位办理时间为\(T_i\)，\(M\)个人办理登机业务，他们可以选择最佳的方案，不考虑换人和换窗口的时间，所有窗口是同时计时的，即同时开始办理业务，请输出所有人都登机的最少时间。

如样例\(1\)：

2个窗口，6个人，第一个窗口的单位时间是7,第二个是10, 一二个人分别在两个窗口办理，7秒时第三个人可在第一个窗口开始办理，10秒时，第四人开始在窗口二办理，时间14时，第五人一窗口。在时间20，窗口2可以使用，如果第六人在此办理，总时间将是30秒，如果等1秒在一窗口办理，则总时间是28秒。

输入：

第一行两个正整数 \(N (1 ≤ N ≤ 100 000)\),

窗口数,和\(M (1 ≤ M ≤ 1 000 000 000)\), 登机人数。

以下每行一个数\(T_i\)表示第\(i\)个窗口的单位办理时间 \((1 ≤ Ti ≤ 10^9)\).

输出 :

一个数，最少办理时间。

input

2 6
7
10

output

28

input

7 10
3
8
3
6
9
2
4

output

8

---

时间就是每个窗口时间的最大值，求最大值的最小值，用二分答案；

\(Code\)

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=100005,M=1000000005;
int n,m;
int a[N],mins=0x7fffffff;
ll l,r;
inline int read()
{
	int x=0,f=1;char st=getchar();
	while(st<'0'||st>'9'){if(st=='-') f=-1;st=getchar();}
	while(st>='0'&&st<='9') x=x*10+st-'0',st=getchar();
	return x*f;
}

inline bool check(ll mid)
{
	ll tmp=0;
	for(int i=1;i<=n;i++)
	{
		tmp+=mid/a[i];
		if(tmp>=m) return 1;
	}
	return 0;
}

int main()
{
	freopen("aerodrom.in","r",stdin);
	freopen("aerodrom.out","w",stdout);
	n=read();m=read();
	for(int i=1;i<=n;i++)
	{
		a[i]=read();
		mins=min(mins,a[i]);
	}
	r=(ll)mins*m;
	while(l<r)
	{
		ll mid=l+r>>1;
		if(check(mid)) r=mid;
		else l=mid+1;
	}
	printf("%lld",l);
	fclose(stdin);
	fclose(stdout);
	return 0;
}

---

T2 HERKABE (trie

TimeLimit: 1000MS

Memory Limit: 32768KB

给出\(N\)个由大写字母构成的名字，现在要求对名字排序，要求有相同前缀的单词要排在一起，问共有多少种排法。

输入：

第一行一个正整数 \(N (3 ≤ N ≤ 3000)\), 名字的个数。

以下N行，每行一个名字长度界于\(1\)到 \(3000\) 名字无重复且按任意顺序给出。.

输出：

一行一个正整数表示方案总数。由于数据大要求输出模\(1000 000 007\)的值.

input

3
IVO
JASNA
JOSIPA

output

4

input

5
MARICA
MARTA
MATO
MARA
MARTINA

output

24

input

4
A
AA
AAA
AAAA

output

8

---

这道题目有故意卡内存之嫌；

先理解题目；

第一个样例对我们没有太大帮助；

第二个样例；

最长的公共前缀是MART,所以MARTA，MARTINA必须排在一起；有\(2!\)种

把这两个看成一个整体\(x\),接下来的最长公共前缀是MAR,所以\(x\),MARICA，MARA必须放在一起；有\(3!\)种；

再把这些看成一个整体\(y\),接下来的最长公共前缀是MA，所以\(y\),MATO必须放在一起；有\(2!\)种；

总共有\(2！*2！*3！=24\)种；

发现，这不就是一颗\(trie\)树吗;

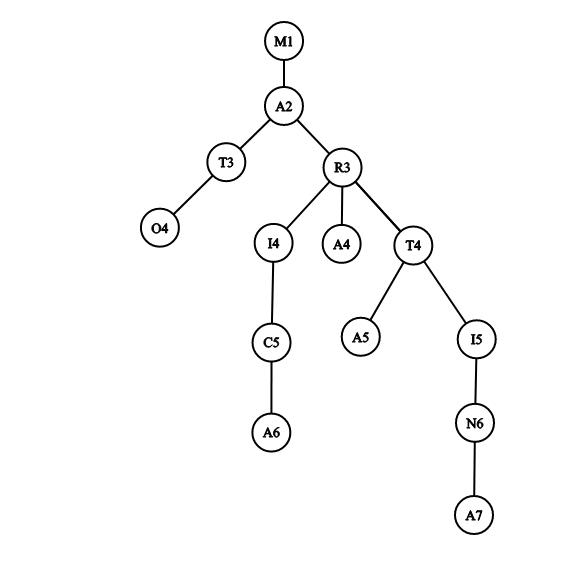
其实答案就是\(trie\)数中，每个节点的子节点个数的阶乘的乘积；

然后写棵\(trie\)就可以了

然后第三个样例过不了，当某个字符串是另一个字符串的前缀时，我们发现这一个字符串是没有结束符的，我们可以在每个字符串后面加一个\('Z'+1\)，这样就不会有任何两个字符串互为前缀了；

然后就会\(MLE\);

时间复杂度是\(O(n^2)\)

优化

• 用vector 代替字符集；
• 排序后模拟\(trie\)树；

这种办法比较好想，想用\(O(n^2logn)\)按字典序排序，有相同前缀的一定在一起；

我们一位一位搜，找下一位有多少种不同的字符(就是\(trie\)树中这个节点的子节点个数)，过程中统计子节点个数的阶乘，当只有一个子节点时返回；

与\(trie\)树时间复杂度一样，这部分是\(O(n^2)\);

\(Code\)

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=3005,mod=1000000007;
int n;
struct skr
{
	char s[N];
	int len;
	bool operator<(skr w)const
	{
		for(int i=0;i<max(len,w.len);i++)
			if(s[i]<w.s[i]) return 1;
			else if(s[i]>w.s[i]) return 0;
	}
}a[N];
ll ans=1,nm[N];
inline int read()
{
	int x=0,f=1;char st=getchar();
	while(st<'0'||st>'9'){if(st=='-') f=-1;st=getchar();}
	while(st>='0'&&st<='9') x=x*10+st-'0',st=getchar();
	return x*f;
}

inline void dfs(int x,int l,int r) //搜第x位，搜索区间是l~r
{
	if(l>=r) return ;
	int num=0;
	int L=l,R=l;
	for(int i=l;i<=r;i++)
	{
		if(a[i].s[x]==a[L].s[x]) R=i;
		else
		{
			num++;
			dfs(x+1,L,R);
			L=i;
		}
	}
	num++;
	if(L==r) R=r;
	dfs(x+1,L,R);
	ans=ans*nm[num]%mod;
}

int main()
{
	freopen("herkabe.in","r",stdin);
	freopen("herkabe.out","w",stdout);
	n=read();
	for(int i=1;i<=n;i++)
	{
		scanf("%s",a[i].s);
		a[i].len=strlen(a[i].s);
		a[i].s[a[i].len]='Z'+1;
		a[i].len++;
	}
	nm[0]=1;
	for(int i=1;i<=n;i++)
		nm[i]=nm[i-1]*i%mod;
	sort(a+1,a+1+n);
	dfs(0,1,n);
	printf("%lld",ans);
	fclose(stdin);
	fclose(stdout);
	return 0;
}

• 压缩\(trie\)树

实际上是压缩尾缀，将没有分叉的节点(单链)合成一个节点，这样建成的\(trie\)树，除了叶子结点，每个节点有最少\(2\)个子节点，最多有字符集大小个子节点。节点个数是字符串个数等级的，可以大规模压缩空间；

​ 比如这是一棵压缩了的\(trie\)树：

（图片来自网络

---

T2 HERKABE (扩展域并查集

TimeLimit: 1000MS

Memory Limit: 32768KB

给出一个数字\(N\)表示有\(N\)个\(32\)位无符号数\((0\sim 2^{32}-1)\)，我们可以进行如下两个操作

操作\(1\)表示把第\(K\)个数后\(M\)位转到最前面；

操作\(2\)表示把第\(K\)个数和第\(L\)个数进行\(XOR\)运算。

我们最初不知道这\(N\)个数的值，但我们知道每一个\(2\)操作后的结果，请推出每一个数最初的值。如果有多种解，输出字典序最小的。（如果第\(K-1\)个数一样，则第\(K\)个数小的则小）

输入 ：

第一行两个正整数: \(N (2 ≤ N ≤ 100 000)\), 变量的个数。和 \(E (1 ≤ E ≤ 100 000)\), 操作的个数。

接下来\(E\)行，按执行的顺序给出每一个操作和操作后的答案。 \((1 ≤ K, L ≤ N, 0 ≤ M < 32)\).

每次操作的答案大小\(0\) 到$ 2^{32}– 1$,二进制异或的值是按\(10\)进制给出的。

输出：

一行，\(N\)个值，表示变量最初的可能值。

如果找不到合适的方案，则输出\(-1\)。

input

3 3
2 1 2
1
2 1 3
2
2 2 3
3

output

0 1 2

input

4 6
2 4 2
3
2 4 1
6
1 3 1
2 3 1
2
1 2 2
2 2 3
7

output

5 0 14 3

input

5 6
2 4 2
10
2 5 3
2
2 2 3
1
2 1 4
3
1 3 1
2 3 4
2147483663

output

 15 6 7 12 5

---

我们先把\(n\)个数拆成\(n\)个二进制串；

从第二种个操作入手，如果得到的结果第\(i\)位是\(1\)，意味着第\(K\)个和第\(L\)个数的第\(i\)位是不一样的，否则是一样的；

那\(1\)操作呢，我们发现它只是把我们的二进制串移了个位置，可以记录一个\(r[i]\)表示第\(i\)个串被右移了多少位；

这样我们得到了很多约束条件，要求一种构造方法，使每个节点有一个合适的赋值（\(0/1\)）;

这就是\(2-SAT\)模型了，但这道题又会\(MLE\);

这类问题也可以用并查集扩展域来做，应为只有两种取值，我们视每个数的每一位为一个节点，每个节点有两个域,\(0\)域和\(1\)域；

如果两个点相同，则把他们的，\(0\)域相连，\(1\)域相连；

代表其中一个节点选\(0(或1)\)，另一个必须选\(0(或1)\);

若不同，则\(1\)域与\(0\)域相连，\(0\)域与\(1\)域相连；

如果有一个节点的\(0\)域与\(1\)域相连了，则输出\(-1\);

确保了有合法构造方案之后，我们可以用贪心得到字典序最小的构造方案；

从第一个数的最高位开始；

优先选\(0\)，如果其\(0\)域的根被取了与它所在域合适的值，当前节点就取\(0\);

\(1\)域同样；

如果两个域都没有合适的值，当前节点优先选\(0\)，并应当把其\(0\)域根节点的取值赋成这个根节点所在域的值，相当于把这个集合的节点都赋了值；

\(Code\)

#include<bits/stdc++.h>
#define c n*32
#define ll long long
using namespace std;
const int N=100005;

int n,e,opt;
char ans[N][35];//卡内存
int r[N];
int fa[N*32*2],f1,f2;
ll sq[35],ra;

inline int read()
{
	int x=0,f=1;char st=getchar();
	while(st<'0'||st>'9'){if(st=='-') f=-1;st=getchar();}
	while(st>='0'&&st<='9') x=x*10+st-'0',st=getchar();
	return x*f;
}

inline int get(int x)
{
	return fa[x]==x?x:fa[x]=get(fa[x]);
}

int main()
{
	freopen("procesor.in","r",stdin);
	freopen("procesor.out","w",stdout);

	n=read();e=read();
	memset(fa,-1,sizeof fa);
	for(int i=0;i<=n*32*2;i++)
		fa[i]=i;
	for(int i=1;i<=e;i++)
	{
		opt=read();
		if(opt==1)
		{
			int x=read(),y=read();
			r[x]=(r[x]+y)%32;
		}
		else
		{
			int x=read(),y=read(),z;
			scanf("%lld",&z);
			for(int j=0;j<32;j++)
				if((z>>j)&1)
				{
					int x1=(j+r[x])%32,x2=(j+r[y])%32;
					f1=get((x-1)*32+x1),f2=get((y-1)*32+x2+c);
					if(f1!=f2)
						fa[f1]=f2;
					f1=get((x-1)*32+x1+c),f2=get((y-1)*32+x2);
					if(f1!=f2)
						fa[f1]=f2;
				}
				else
				{
					int x1=(j+r[x])%32,x2=(j+r[y])%32;
					f1=get((x-1)*32+x1),f2=get((y-1)*32+x2);
					if(f1!=f2)
						fa[f1]=f2;
					f1=get((x-1)*32+x1+c),f2=get((y-1)*32+x2+c);
					if(f1!=f2)
						fa[f1]=f2;
				}
		}
	}
	for(int i=0;i<32*n;i++)
	{
		f1=get(i),f2=get(i+c);
		if(f1==f2)
		{
			printf("-1");
			fclose(stdin);
			fclose(stdout);
			return 0;
		}
	}
	for(int j=1;j<=n;j++)
		for(int i=0;i<32;i++)
			ans[j][i]=2;//初始
	for(int j=1;j<=n;j++)
		for(int i=31;i>=0;i--)
		{
			bool fl1=0,fl2=0;
			f1=get((j-1)*32+i);//0
			f2=get((j-1)*32+i+c);//1
			if(f1>=c) f1-=c,fl1=1;
			if(f2>=c) f2-=c,fl2=1;
			if(ans[(f1)/32+1][f1%32]==(fl1==1))
			{
				ans[j][i]=0;
			}
			else
			{
				if(ans[(f2)/32+1][f2%32]==(fl2==1))
					ans[j][i]=1;
				else
				{
					ans[j][i]=0;
						ans[(f1)/32+1][f1%32]=fl1;
				}
			}
		}
	sq[0]=1;
	for(int i=1;i<=32;i++)
		sq[i]=sq[i-1]*2;
	for(int j=1;j<=n;j++)
	{
		ra=0;
		for(int i=0;i<32;i++)
		{
			ra=ra+sq[i]*ans[j][i];
		}
		printf("%lld ",ra);
	}

	fclose(stdin);
	fclose(stdout);
	return 0;
}