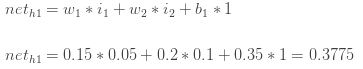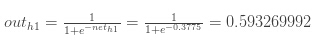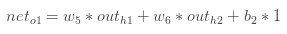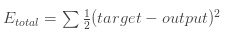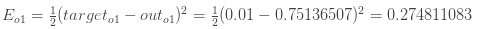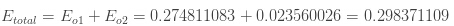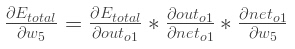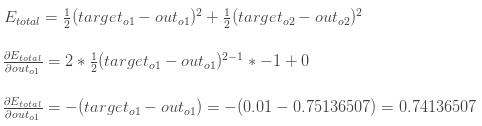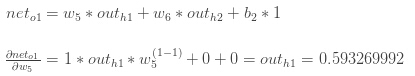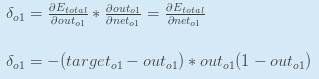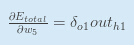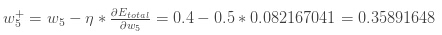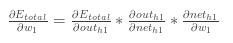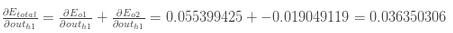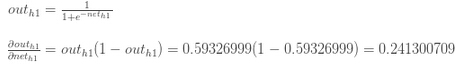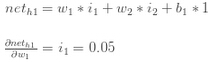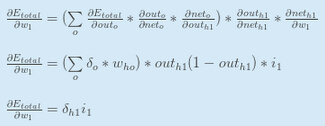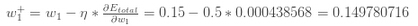CNN反向传播更新权值

背景

反向传播(Backpropagation)是训练神经网络最通用的方法之一，网上有许多文章尝试解释反向传播是如何工作的，但是很少有包括真实数字的例子，这篇博文尝试通过离散的数据解释它是怎样工作的。

Python实现的反向传播

你能使用Python来实现反向传播，我曾经在this Github repo上实现了反向传播算法。

反向传播的可视化

显示神经网络学习时相互作用的可视化，检查我的Neural Network visualization。

另外的资源

如果你发现这个教程对你有用并且想继续学习神经网络以及它的应用，我强烈建议你看Adrian Rosebrock优秀的教程Getting Started with Deep Learning and Python。

概述

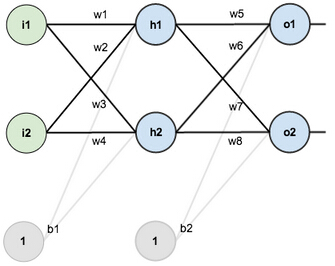
对于这个教程，我们将使用2个输入神经元、2个隐含层神经元以及2个输出层神经元组成一个神经网络，另外，隐含层和输出层神经元各包含一个偏差。

这是基本结构：

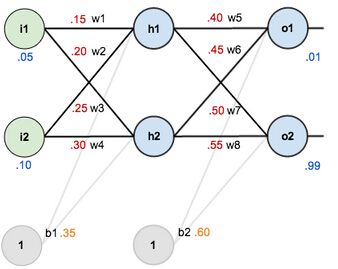
目的让神经网络工作，我们对权重、偏差和训练的输入/输出设置一个初始值：

反向传播的目的是优化权重，以便于让神经网络学习怎样正确的把任意的输入映射到输出中。

这篇教程的剩余部分我们将要和单一的训练集工作：输入0.05和0.10，我们想要神经网络输出0.01和0.99。

前向反馈

为了开始，当前给定权重和偏差以及输入值0.05和0.10，神经网络预测结果是什么，我们需要把输入值向前传给网络。

我们知道全部的输入值传到每个隐含层神经元中，使用激活函数挤压全部的输入值(在这里，我们使用logistic函数)，对输出层神经元重复这一过程。

计算h1" role="presentation" style="position: relative;">h1h1的输入：

然后我们利用logistic函数把neth1" role="presentation" style="position: relative;">neth1neth1挤压到h1" role="presentation" style="position: relative;">h1h1的输出：

对h2" role="presentation" style="position: relative;">h2h2进行相同的操作：

outh2=0.596884378" role="presentation" style="position: relative;">outh2=0.596884378outh2=0.596884378

对输出层神经元重复操作，使用隐含层神经元的输出作为输出层神经元的输入。

这是o1" role="presentation" style="position: relative;">o1o1的输出：

对o2" role="presentation" style="position: relative;">o2o2进行相同操作：

outo2=0.772928465" role="presentation" style="position: relative;">outo2=0.772928465outo2=0.772928465

计算整体误差

利用平方和误差，我们能计算每个输出层神经元的误差：

例如，目标输出o1" role="presentation" style="position: relative;">o1o1是0.01，但是神经网络输出是0.75136507，因此误差是：

对o2" role="presentation" style="position: relative;">o2o2重复这个过程：

Eo2=0.023560026" role="presentation" style="position: relative;">Eo2=0.023560026Eo2=0.023560026

神经网络整体误差：

反向传播

反向传播的目的是更新网络中每个权重，以便他们真实的输出值是接近目标输出，从而最小化输出层神经元的误差。

输出层

考虑w5" role="presentation" style="position: relative;">w5w5，我们想要知道w5" role="presentation" style="position: relative;">w5w5怎样影响整体误差，即αEtotalαw5" role="presentation" style="position: relative;">αEtotalαw5αEtotalαw5

应用链式规则：

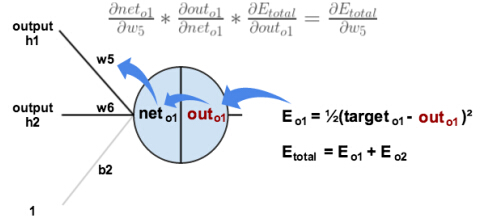
可视化我们正在做的：

我们需要理解这个公式的每一步。

首先，output怎样改变整体误差？

下一步，net input怎样改变o1" role="presentation" style="position: relative;">o1o1输出？

logistic函数的偏导数是输出乘以1减输出：

最后，w5" role="presentation" style="position: relative;">w5w5怎样改变o1" role="presentation" style="position: relative;">o1o1的net input？

把它们结合起来：

你常常能看到delta rule的结合形式：



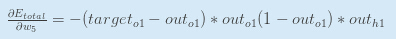
我们利用αEtotalαouto1" role="presentation" style="position: relative;">αEtotalαouto1αEtotalαouto1和αouto1αneto1" role="presentation" style="position: relative;">αouto1αneto1αouto1αneto1来重写αEtotalαneto1" role="presentation" style="position: relative;">αEtotalαneto1αEtotalαneto1，我们使用这个重新上面的表达式：

因此：

为了减少误差，我们从当前权重减去这个值(乘以一个学习率，设置成0.5)：

我们能重复这个过程得到新的权重w6" role="presentation" style="position: relative;">w6w6，w7" role="presentation" style="position: relative;">w7w7和w8" role="presentation" style="position: relative;">w8w8：

当我们继续下面的反向传输算法时，我们使用初始权重，而不是更新过的权重。

隐含层

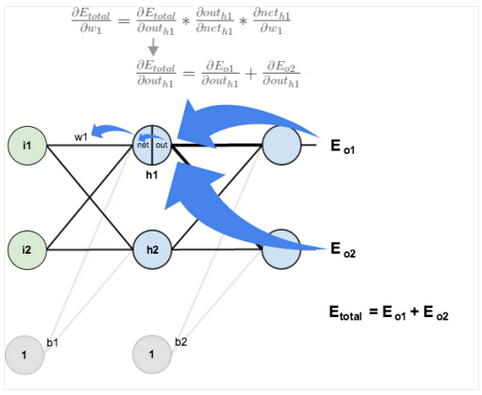
下一步，我们将继续向后计算w1" role="presentation" style="position: relative;">w1w1，w2" role="presentation" style="position: relative;">w2w2，w3" role="presentation" style="position: relative;">w3w3和w4" role="presentation" style="position: relative;">w4w4新值，这是我们需要理解的：

可视化：

我们将要对隐含层神经元使用相似的过程，但是稍微不同的是，每个隐含层神经元的输出贡献到多个输出层神经元中。我们知道outh1" role="presentation" style="position: relative;">outh1outh1影响outo1" role="presentation" style="position: relative;">outo1outo1和outo2" role="presentation" style="position: relative;">outo2outo2，因此αEtotalαouth1" role="presentation" style="position: relative;">αEtotalαouth1αEtotalαouth1需要考虑两个输出层神经元的影响：

αEtotalαouth1=αEo1αouth1+αEo2αouth1" role="presentation" style="position: relative;">αEtotalαouth1=αEo1αouth1+αEo2αouth1αEtotalαouth1=αEo1αouth1+αEo2αouth1

先计算αEo1αouth1" role="presentation" style="position: relative;">αEo1αouth1αEo1αouth1:

αEo1αouth1=αEo1αneto1∗αneto1αouth1" role="presentation" style="position: relative;">αEo1αouth1=αEo1αneto1∗αneto1αouth1αEo1αouth1=αEo1αneto1∗αneto1αouth1

使用稍早前计算的值来计算αEo1αneto1" role="presentation" style="position: relative;">αEo1αneto1αEo1αneto1：

αEo1αneto1=αEo1αouto1∗αouto1αneto1=0.74136507∗0.186815602" role="presentation" style="position: relative;">αEo1αneto1=αEo1αouto1∗αouto1αneto1=0.74136507∗0.186815602αEo1αneto1=αEo1αouto1∗αouto1αneto1=0.74136507∗0.186815602

αneto1αouth1" role="presentation" style="position: relative;">αneto1αouth1αneto1αouth1等于w5" role="presentation" style="position: relative;">w5w5:

neto1=w5∗outh1+w6∗outh2+b2∗1" role="presentation" style="position: relative;">neto1=w5∗outh1+w6∗outh2+b2∗1neto1=w5∗outh1+w6∗outh2+b2∗1

αneto1αouth1=w5=0.40" role="presentation" style="position: relative;">αneto1αouth1=w5=0.40αneto1αouth1=w5=0.40

合在一起：

αEo1αouth1=αEo1αneto1∗αneto1αouth1=0.138498562∗0.40=0.055399425" role="presentation" style="position: relative;">αEo1αouth1=αEo1αneto1∗αneto1αouth1=0.138498562∗0.40=0.055399425αEo1αouth1=αEo1αneto1∗αneto1αouth1=0.138498562∗0.40=0.055399425

对αEo2αouto1" role="presentation" style="position: relative;">αEo2αouto1αEo2αouto1做相同的处理：

αEo2αouth1=−0.019049119" role="presentation" style="position: relative;">αEo2αouth1=−0.019049119αEo2αouth1=−0.019049119

因此：

现在我们有αEtotalαouth1" role="presentation" style="position: relative;">αEtotalαouth1αEtotalαouth1，我们还需要计算αouth1αneth1" role="presentation" style="position: relative;">αouth1αneth1αouth1αneth1，然后对每个权重计算αneth1αw" role="presentation" style="position: relative;">αneth1αwαneth1αw：

我们计算h1" role="presentation" style="position: relative;">h1h1对w1" role="presentation" style="position: relative;">w1w1的偏导数：

把它们结合起来：

你也可以如下写：

现在我们能更新w1" role="presentation" style="position: relative;">w1w1：

对w2" role="presentation" style="position: relative;">w2w2，w3" role="presentation" style="position: relative;">w3w3和w4" role="presentation" style="position: relative;">w4w4重复上面过程：

最后，我们更新所有权重，当我们把输入0.05和0.1向前反馈，神经网络的误差为0.298371109，在一次反向传播后，整体误差降到0.291027924，它看似不多，但是重复10000次之后，误差大幅下降到0.000035085，在这之后，我们把输入0.05和0.1向前反馈，那么输出的2个神经元生成0.015912196(vs 目标0.01)和0.984065734(vs 目标0.99)。

原文链接：A Step by Step Backpropagation Example

转https://blog.csdn.net/shaomingliang499/article/details/50587300