三维动画形变算法（Laplacian-Based Deformation）

　　网格上顶点的Laplace坐标（均匀权重）定义为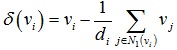：，其中d_i为顶点v_i的1环邻域顶点数。

　　网格Laplace坐标可以用矩阵形式表示：△=LV，其中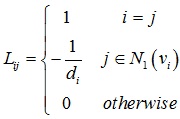，那么根据网格的Laplace坐标通过求解稀疏线性方程组可以得到网格的顶点坐标。

　　基于网格Laplace形变算法的思想：网格上顶点的Laplace坐标作为网格的细节特征，其在网格形变前后的局部坐标系内不发生变化。Laplace形变问题可以用如下数学优化形式表达，那么问题的关键是如何得到网格形变后的Laplace坐标，或者说是每个顶点Laplace坐标的变换T_i。

　　文章[Lipman et al. 2004]形变算法主要包括以下步骤：

　　1.在初始网格顶点上建立局部坐标系，先利用原始Laplace坐标将网格进行形变；

　　2.在形变后的网格顶点上建立局部坐标系，根据形变前后Laplace坐标在局部坐标系内不变，估计形变后网格顶点的Laplace坐标，如下：

δ(v_j)=αn_j+βu_ji+γ(n_j×u_ji)

δ(v_j’)=αn_j’+βu_ji’+γ(n_j’×u_ji’)

其中：n_j和n_j’为形变前后顶点v_j的法向，u_ji和u_ji’为形变前后边ji在顶点v_j切平面内的投影方向，δ(v_j)和δ(v_j’)为形变前后顶点v_j的Laplace坐标。

　　3.根据编辑后的Laplace坐标求解形变后网格的顶点坐标。

　　步骤2和步骤3可以进行迭代。

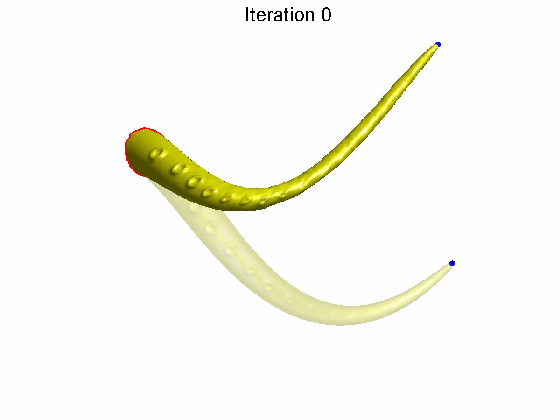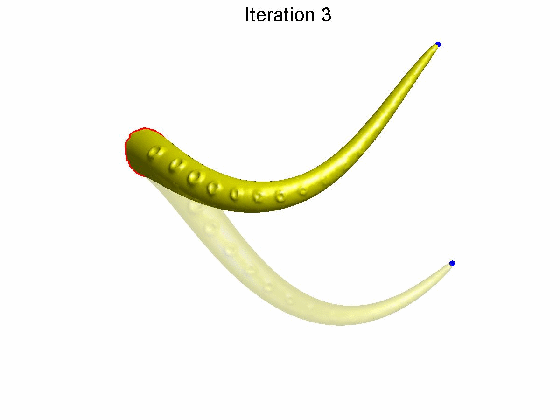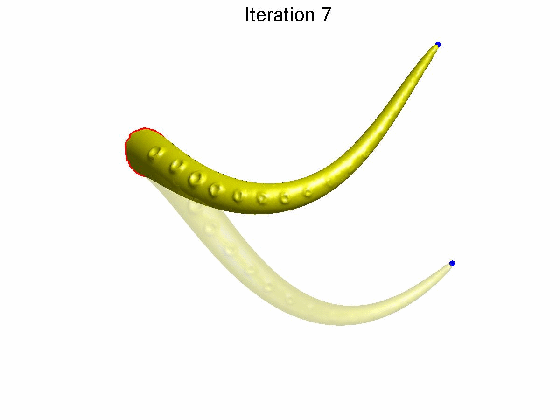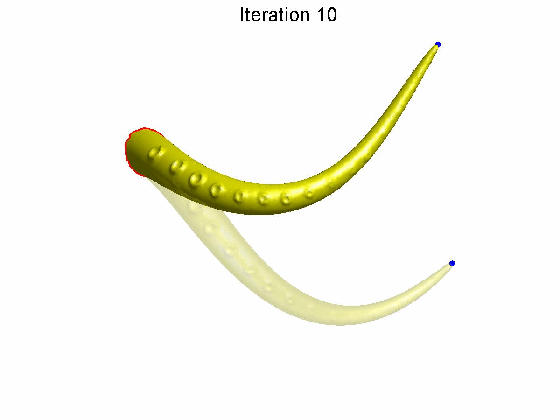
　　算法效果：拖动蓝色控制点后，发现随着算法迭代次数的增加，网格表面细节特征逐渐恢复。

　　文章[Sorkine et al. 2004]形变算法是将优化表达式中T_i表示成v_i’相关的形式，这样就可以直接求解得到形变后网格顶点坐标v_i’，不需要迭代求解，具体过程如下：

T_i在小角度情况下可以近似为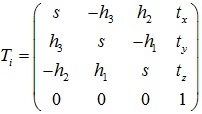：，将T_i表示v_i’线性相关的形式：

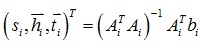
其中：。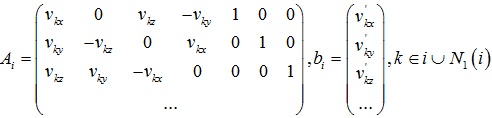

　　这样T_i就表示成了v_i’线性相关的形式，然后根据优化表达式通过最小二乘法即可求得v_i’。

　　算法效果：蓝色控制点从下向上拖拽时的网格形变效果。

　　前文介绍的Possion形变和Laplace形变是基于网格表面的形变，在大尺度网格形变时，算法不保证体图细节。文章[Zhou et al. 05]提出了基于体图的Laplace形变算法，对于输入网格M，构造两种体图：填充网格内部的图g_in用来防止大尺度形变时不自然的体积变化；覆盖网格外侧的图g_out用来防止局部自交。

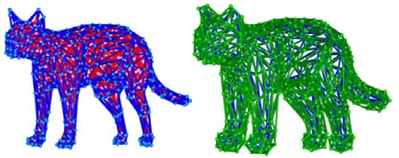
蓝色为输入网格M；红色为填充网格内部的图g_in；绿色为覆盖网格外侧的图g_out

　　为了平衡保持网格表面几何细节和保持体图几何细节两个目标，优化函数修改为以下形式：

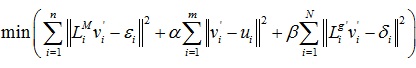
其中，图g的前n个点就是网格M的点。L^M是网格的离散Laplace算子；g’是去掉M中的边之后的g的子图；对网格M中的点，ε_i(1≤i≤n)是形变后网格的Laplace坐标；对子图g’中的点，δ_i(1≤i≤N)是形变后体图的Laplace坐标。形变能量分为三个部分，分别刻画保持表面几何细节、满足用户指定约束和保持体图细节的程度。

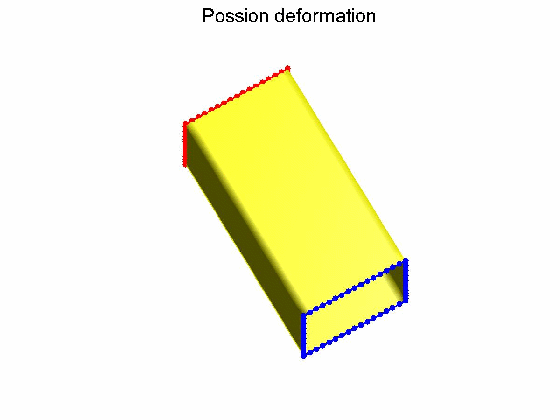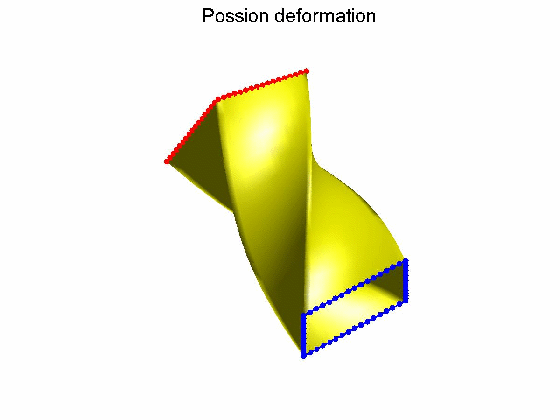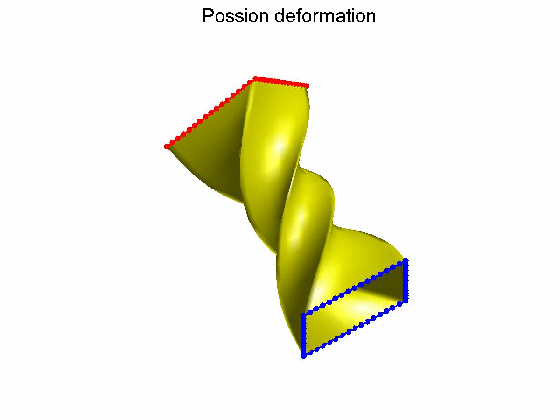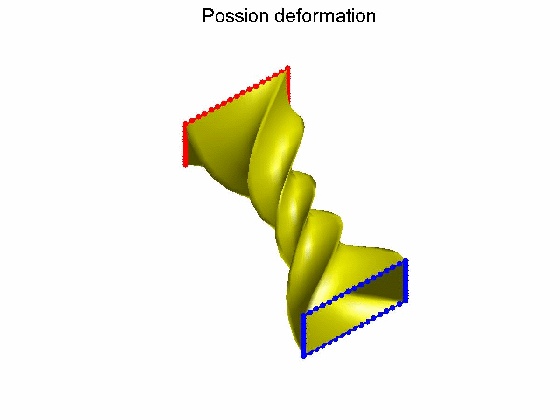
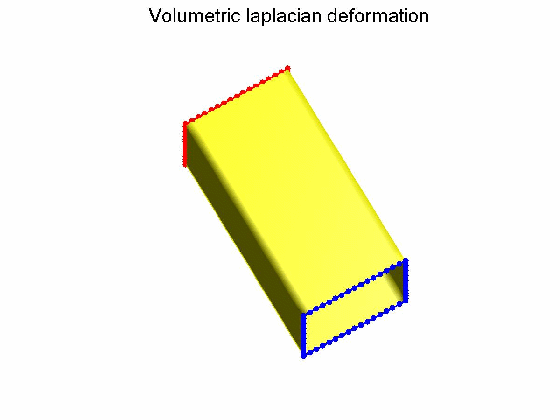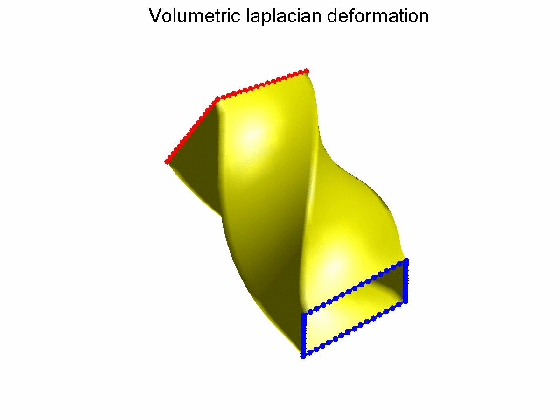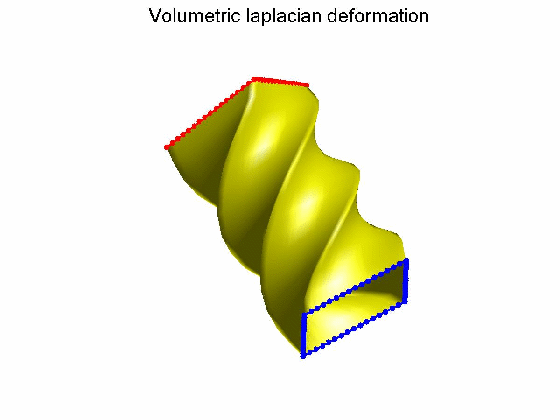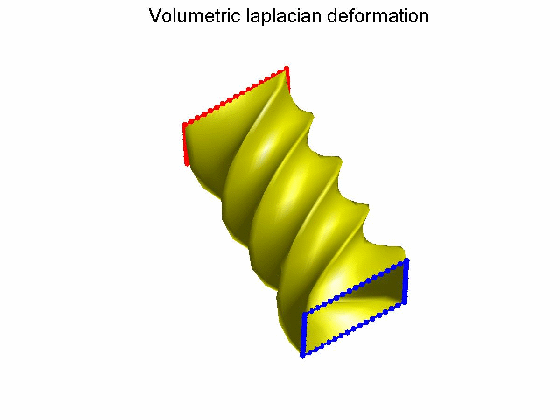
　　算法效果：Possion形变不保持体图细节，Volumetric laplacian形变保持体图细节。

本文为原创，转载请注明出处：http://www.cnblogs.com/shushen。

参考文献：

[1] Y. Lipman, O. Sorkine, D. Cohen-Or, D. Levin, C. Rossl, and H.-P. Seidel. "Differential Coordinates for Interactive Mesh Editing." In Proc. of Shape Modeling International, pp.181-90. Washington, DC: IEEE Computer Society, 2004.

[2] O. Sorkine, D. Cohen-Or, Y. Lipman, M. Alexa, C. Rossl, and H.-P. Seidel. "Laplacian Surface Editing." In Proc. of Eurographics Symposium on Geometry Processing, pp. 179-88. Aire-la-Ville, Switzerland: Eurographics Association, 2004.

[3] K. Zhou, J. Huang, J. Snyder, X. Liu, H. Bao, B. Guo, and H.-Y.Shum. "Large Mesh Deformation Using the Volumetric Graph Laplacian." ACM Transactions on Graphics (Proc. SIGGRAPH) 24:3 (2005), 496-503.

[4] 黄劲. 大尺度几何形变理论与方法[D]. 浙江大学, 2007.