『嗨威说』算法设计与分析 - PTA 数字三角形 / 最大子段和 / 编辑距离问题（第三章上机实践报告）

本文索引目录：

一、PTA实验报告题1 ： 数字三角形

　　1.1　　实践题目

　　1.2　　问题描述

　　1.3　　算法描述

　　1.4　　算法时间及空间复杂度分析

二、PTA实验报告题2 ： 最大子段和

　　2.1　　实践题目

　　2.2　　问题描述

　　2.3　　算法描述

　　2.4　　算法时间及空间复杂度分析

三、PTA实验报告题3 ： 编辑距离问题

　　3.1　　实践题目

　　3.2　　问题描述

　　3.3　　算法描述

　　3.4　　算法时间及空间复杂度分析

四、实验心得体会（实践收获及疑惑）

一、PTA实验报告题1 ： 数字三角形

　　1.1　　实践题目：

　　1.2　　问题描述：

　　　　　题意是，题干给你一个三角形（实际上就是半个矩形即下三角形模式或上三角形模式），要求你从顶部计算出到底部最佳的路线，使得经过的数字总和最大。

　　1.3　　算法描述：

这道题很明显需要用到动态规划的方法，存在重叠子问题，因此我们需要找出这道题的动态转移方程。

我们通过模拟可以发现，样例最佳的行走路径是：

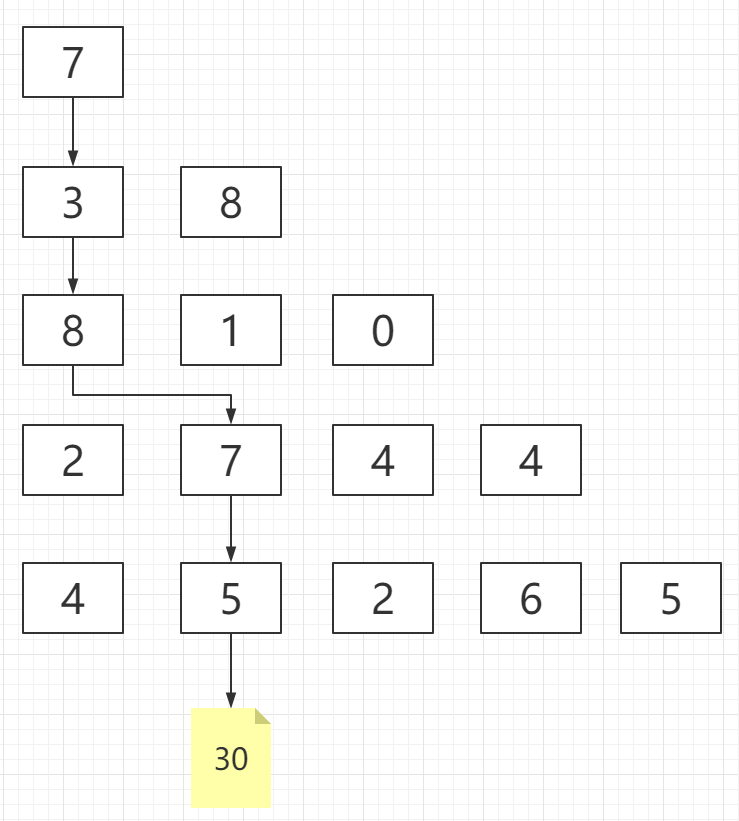
很明显发现，我们并不能通过贪心算法来做这道题，只能用动态规划找出最佳路径。

首先我们需要建立dp数组，定义dp数组的含义为：截至当前位置已走过的数的总和，我们先初始化dp数组。

要确认当前位置，也就需要定义成二维数组，第一个指定为行，第二个指定为具体列。

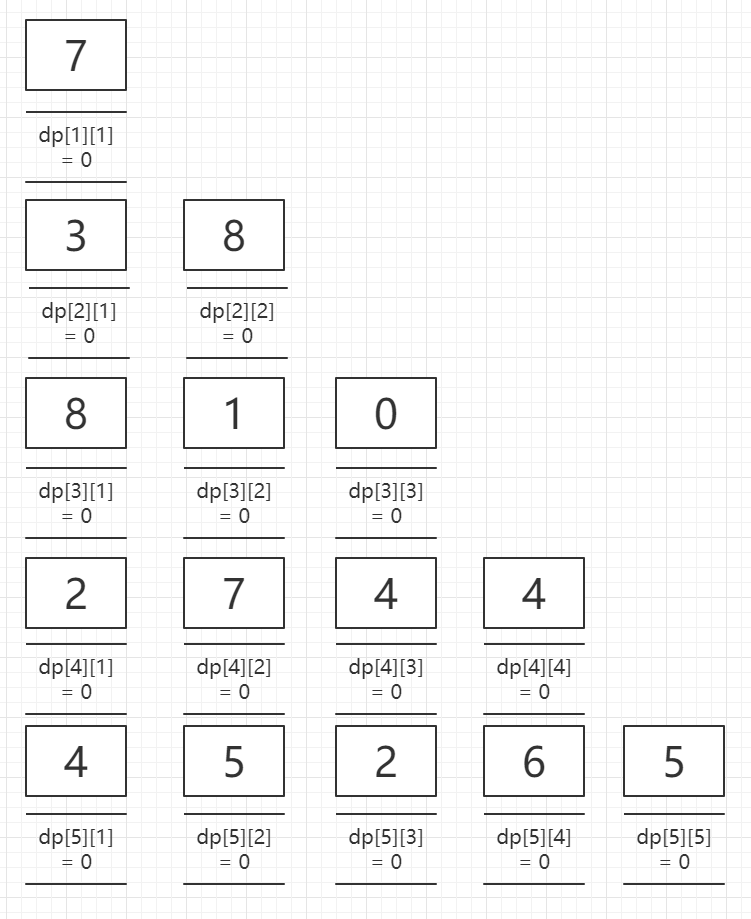
第二步，我们需要确定动态方程，很明显我们知道：

方程为：dp[i][j] = temp[i][j] + max(dp[i+1][j],dp[i+1][j+1])

以最后两列为例，模拟动规过程：

可以很明显的发现，当下面两格相比，取出最大值，加上自己本身，就是当前的dp值，依照这个思路

我们可以把整个dp过程模拟完成：

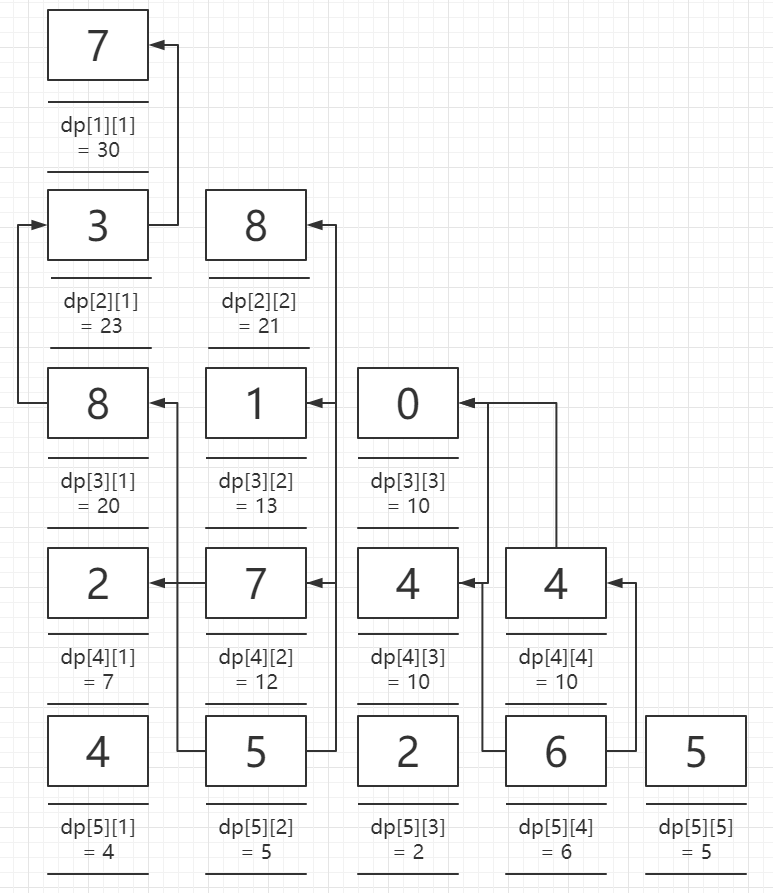
到此模拟完成，我们可以很清楚的看到，我们最终想要的答案，就在最顶层，dp[1][1]中，我们只需要固定输出这个值即可得到答案。

第三步，确认我们的填表顺序，从以上的分析角度可以知道，dp方程中当前dp依赖于当前位置的下一行同列以及下一行同列+1的位置，所以需要从下往上填表，分析完毕，按着这个思路敲出代码即可，

完整代码展示如下：

#include<bits/stdc++.h>
using namespace std;
int n,temp[][],ans = ;
int main()
{
    /* input */
    cin>>n;
    for(int i = ;i<=n;i++)
        for(int j = ;j<=i;j++)
            cin>>temp[i][j];

    /* 动规转移方程： dp[i][j] = temp[i][j] + max(dp[i+1][j],dp[i+1][j+1]);*/

    /* down to up */
    for(int i = n;i>;i--)
        for(int j = ;j<=i;j++)
            temp[i][j] = temp[i][j] + max(temp[i+][j],temp[i+][j+]);

    /* answer */
    cout<<temp[][];
 } 

　　1.4　　算法时间及空间复杂度分析：

　　　整体算法上看，动态规划是不计算重复子问题，并优化计算过程，防止计算重复，经过分析可知，我们需要O（n^2）时间初始化dp数组，需要O（1/2 * n^2）的时间进行填表，最后输出，总的来看时间复杂度为O（n^2）。

　　　动态规划需要用到辅助空间二维数组进行填表，表的大小根据问题规模确定，因此空间复杂度是O（n^2）。

二、PTA实验报告题2 ： 最大子段和

　　2.1　　实践题目：

　　2.2　　问题描述：

　　　　第二题是动态规划的小小压缩版本，题意是说给一段序列，求怎么取一小段，使得加和数最大，也即最大子段和问题。

　　2.3　　算法描述：

　　　　首先，分析题目选择相应算法，虽然这章都是在学动态规划，但是在平时拿到题目的时候，我们是不知道这是动态规划的，所以需要分析问题，一般这种求最值问题，常常先考虑贪心能否使用，可以发现这道题是可以使用贪心算法的，所以我也使用贪心算法写了一次，但是呢鉴于题目要求需要O（n）的时间复杂度，因此优先考虑动态规划啦。

　　　  第二，初始化dp数组，定义dp数组dp[i]为从1到i中最大的子段和。

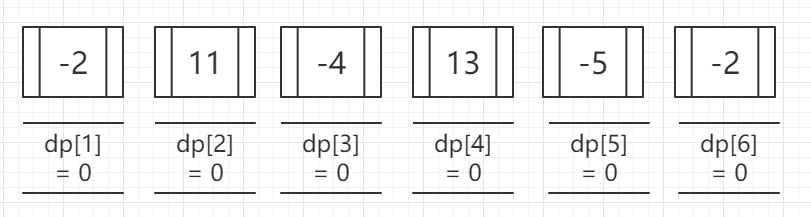
　　　   第三，动态规划转移方程，明显可以知道：dp[ i ] = max( dp[ i-1 ] , k ) ; k 为从0-i的加和大于0的子段，一旦小于0就从当前位置重新计段长。

　　　　模拟过程如下：

　　因此我们就可以很愉快的写出代码啦。AC代码如下：

#include<bits/stdc++.h>
using namespace std;
int n,temp[],dp[],flag = ,k;
int main()
{
    /* input */
    cin>>n;
    for(int i = ;i<=n;i++)
    {
        cin>>temp[i];
        if(temp[i] >=) flag = ;
    }

    /*    dp[i]:1-i中最大子段和
        k: k从0到i加和大于0的子段，遇到子段小于0的扔掉重新开始计长度*/
    for(int i = ;i<=n;i++)
    {
        if(k>) k += temp[i];
        else k=temp[i];
        dp[i] = max(dp[i-], k);
    }

    /* answer */
    if(flag == ) cout<<;
    else cout<<dp[n];
    return ;
}

　　2.4　　算法时间及空间复杂度分析：

　　　　算法复杂度跟题目要求一致，时间复杂度为O(n)。

　　　　空间复杂度需要一个一维数组dp，因此空间复杂度也是O（n）

三、PTA实验报告题3 ： 编辑距离问题

　　3.1　　实践题目：

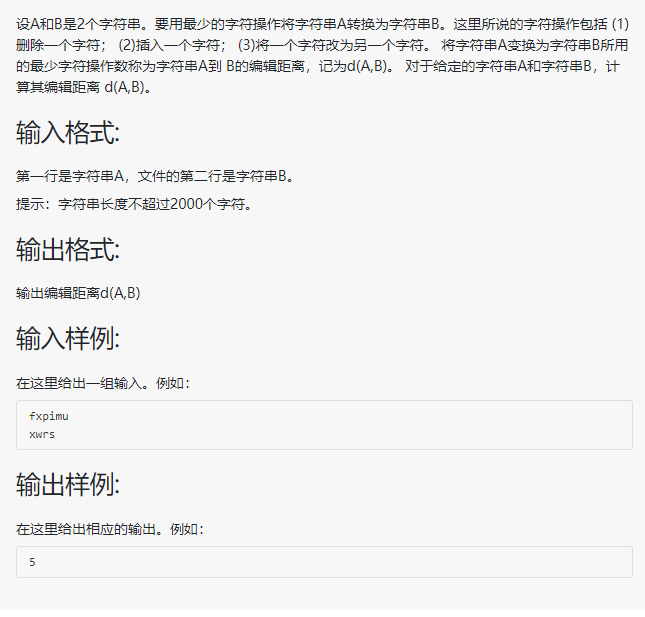
　　3.2　　问题描述：

　　　　该题目为：题目意思是给定两端英文序列，要求将A序列变成B序列，可以通过对A进行删除、插入、更换任意字符，得到B序列，要求以最少步骤为准。

　　3.3　　算法描述：

　　　　这道题我和三木在写的时候第一次没有写出来，三木想到一个绝佳的数学公式，用最大长度字符串长减去LCS即为所求，但是答案WA在了第三点，后来发现存在特例无法解决，所以课后我又换了一种方式，这里我讲解的还不是很好，在一个博客我看到一个非常完整很棒的讲解，贴出来给大家看看吧：

　　https://blog.csdn.net/weixin_42681158/article/details/89411572

　　我的AC代码如下：

#include<bits/stdc++.h>
using namespace std;
int dp[][];
char a[];
char b[];
int minval(int a,int b,int c){
    int temp = max(a,b);
    return max(temp,c);
}
int LCS(char *a,char *b)
{
    memset(dp,,sizeof(dp));
    int lena=strlen(a);
    int lenb=strlen(b);
    for(int i=;i<=lena;i++)
    {
        for(int j=;j<=lenb;j++)
        {
            if(a[i-]==b[j-])
                dp[i][j]=minval(dp[i-][j],dp[i][j-],dp[i-][j-]+);
            else
                dp[i][j]=minval(dp[i-][j],dp[i][j-],dp[i-][j-]);
        }
    }
    return dp[lena][lenb];
}

int main()
{
    cin>>a;
    getchar();
    cin>>b;
    int maxss =max(strlen(a),strlen(b));

    cout<<maxss-LCS(a,b);

    return ;
}

　　3.4　　算法时间及空间复杂度分析：

　　　　由分析易知，时间复杂度和空间复杂度均为O（n^2）

四、实验心得体会（实践收获及疑惑）：

　　经过第一次实践合作之后，第二次的实践合作愈发顺利，虽然第三题有一小点WA了，不过还是很合作默契的哈哈。（主要是三木太强了）

简单通过书本和博客总结了一下动态规划的一些基本特点如下：

===动态规划问题的特点：

（1）最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。

（2）重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）

===动规解题的一般思路：

　　动态规划所处理的问题是一个多阶段决策问题，一般由初始状态开始，通过对中间阶段决策的选择，达到结束状态。这些决策形成了一个决策序列，同时确定了完成整个过程的一条活动路线(通常是求最优的活动路线)。

　　动态规划的设计都有着一定的模式，一般要经历以下几个步骤。

　　　　初始状态→│决策１│→│决策２│→…→│决策ｎ│→结束状态

　 （1）划分阶段：按照问题的时间或空间特征，把问题分为若干个阶段。在划分阶段时，注意划分后的阶段一定要是有序的或者是可排序的，否则问题就无法求解。

　 （2）确定状态和状态变量：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然，状态的选择要满足无后效性。

　 （3）确定决策并写出状态转移方程：因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策，状态转移方程也就可写出。但事实上常常是反过来做，根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。

　 （4）寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件。

如有错误不当之处，烦请指正。