算法-一步步教你如何用c语言实现堆排序（非递归）

看了左神的堆排序，觉得思路很清晰，比常见的递归的堆排序要更容易理解，所以自己整理了一下笔记，带大家一步步实现堆排序算法

首先介绍什么是大根堆：每一个子树的最大值都是子树的头结点，即根结点是所有结点的最大值

堆排序是基于数组和二叉树思想实现的（二叉树是脑补结构，实际是数组）

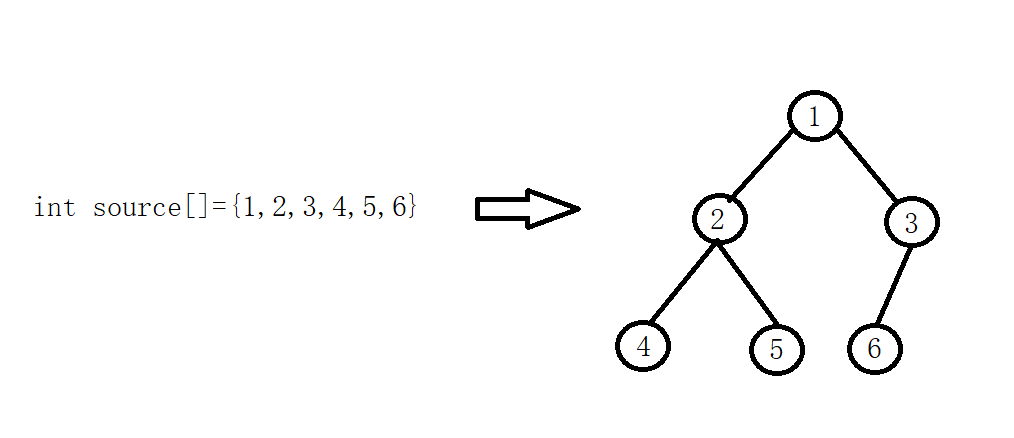
堆排序过程

1、数组建成大根堆，首先，遍历所有结点，当前结点index和父结点（index-1）/ 2 比较 （当前数组的下标是index，此结点的父结点的下标就是（index-1）/ 2  ），如果比父结点大，交换，变成父结点的位置再和上一层的父结点比较，直到满足大根堆条件

int swap(int source[], int a, int b)
{
    int temp = source[a];
    source[a] = source[b];
    source[b] = temp;
}
int heapsort(int source[], int len)
{
    for (int i = ; i <len; i++)
    {
        heapInsert(source, i);
    }
}
int heapInsert(int source[], int index)
{
    while (source[index] > source[(index - ) / ])
    {
        swap(source, index, (index - ) / );
        index = (index - ) / ;
    }
}

2、让根结点和最后一个结点交换位置，也就是数组的第一个数和最后一个数交换位置，接下来最后一个数不用考虑了，比如一个数组有5个数，定义一个变量size=5，大根堆的根结点放到最后一个数后，--size

int size = len;
swap(source, , --size);

3、让交换后的头结点经历一个向下的调整，让结点和自己的两个孩子比较，如果孩子的值比头结点大，交换，交换到孩子结点位置，继续和下面的两个孩子比较，直到满足大根堆条件

int heapify(int source[], int index, int size)//index表示要和它两个孩子比较的结点
{
    int left = index *  + ;  //找到index左孩子结点的数组下标
    while (left < size)
    {
        int largest = left +  < size && source[left + ] > source[left] ? source[left + ] : source[left];//如果有右孩子且右孩子比左孩子大，令largest=右孩子的值，也就是把两个孩子中最大的一个数赋给largest
        if (source[index] < source[largest])
        {
            swap(source, index, largest);
            index = largest;
            left = index *  + ;
        }
        else break;
    }

}

4、重复第2步，第3步，直到size = 0 ，整个数组排序过程结束

while (size > )
    {
        swap(source, , --size);
        heapify(source, , size);
    }

源代码如下

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int swap(int source[], int a, int b)
{
    int temp = source[a];
    source[a] = source[b];
    source[b] = temp;
}
int heapsort(int source[], int len)
{
    for (int i = ; i < len; i++)
    {
        heapInsert(source, i);
    }
    int size = len;
    while (size > )
    {
        swap(source, , --size);
        heapify(source, , size);
    }
}
int heapInsert(int source[], int index)
{
    while (source[index] > source[(index - ) / ])
    {
        swap(source, index, (index - ) / );
        index = (index - ) / ;
    }
}
int heapify(int source[], int index, int size)//index表示要和它两个孩子比较的结点
{
    int left = index *  + ;  //找到index左孩子结点的数组下标
    while (left < size)
    {
        int largest = left +  < size && source[left + ] > source[left] ? left +  : left;//如果有右孩子且右孩子比左孩子大，令largest=右孩子的值，也就是把两个孩子中最大的一个数赋给largest
        if (source[index] < source[largest])
        {
            swap(source, index, largest);
            index = largest;
            left = index *  + ;
        }
        else break;
    }

}
int main()
{
    int source[] = { ,,,,,,,,,,,,,,,,, };
    int len;
    len = sizeof(source) / sizeof(int);
    heapsort(source, len);
    for (int i = ; i < len; i++)
    {
        printf("%d ", source[i]);
    }

}

输出结果

以上就是堆排序的所有细节，这个版本很优良，堆排序的额外空间复杂度是O(1)，如果用递归的话，递归有递归栈，额外空间复杂度不就上去了吗，设计成这种迭代的可以省空间，时间复杂度为O（n log n）

转载请注明出处、作者  谢谢