Dijkstra算法依据项目改进版，输出路径

package dijkstra;

import java.util.ArrayList;

public class Dijkstra {

    private static int N = ;
    /*private static int[][] Graph = {
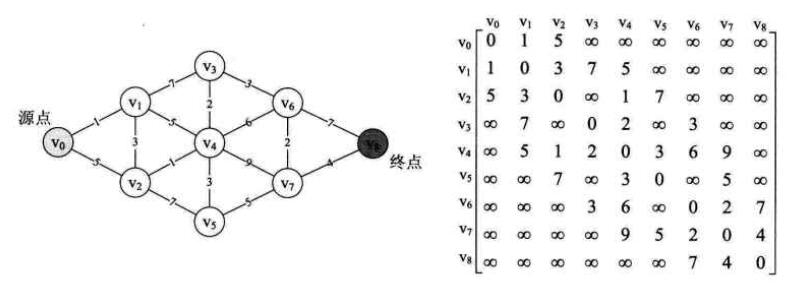
            { 0, 1, 5, N, N, N, N, N, N },
            { 1, 0, 3, 7, 5, N, N, N, N },
            { 5, 3, 0, N, 1, 7, N, N, N },
            { N, 7, N, 0, 2, N, 3, N, N },
            { N, 5, 1, 2, 0, 3, 6, 9, N },
            { N, N, 7, N, 3, 0, N, 5, N },
            { N, N, N, 3, 6, N, 0, 2, 7 },
            { N, N, N, N, 9, 5, 2, 0, 4 },
            { N, N, N, N, N, N, 7, 4, 0 } };*/

    private static int[][] Graph = {
            { , , , N, N, , N, N, N },
            { , , N, N, N, N, , N, N },
            { , N, , , , N, N, N, N },
            { N, N, , , N, N, N, N, N },
            { N, N, , N, , N, N, , N },
            { , N, N, N, N, , N, N, N },
            { N, , N, N, N, N, , , N },
            { N, N, N, N, , N, , ,  },
            { N, N, N, N, N, N, N, ,  } };
    public static void main(String[] args) {
        dijkstra(, Graph,);
    }

    /**
     * Dijkstra最短路径。
     * 即图中"节点vs"到其它各个节点的最短路径。
     * @param vs 起始节点
     * @param Graph 图
     * @param ds 目的终点
     * 输入vs,Graph,ds输出选出的路径
     * 每次选出一个最优节点加入最短路径数组中
     */
    public static void dijkstra(int vs, int[][] Graph,int ds) {
        int NUM = Graph[].length;
        // 前驱节点数组
        int[] prenode = new int[NUM];
        // 最短距离数组
        int[] mindist = new int[NUM];
        // 该节点是否已经找到最短路径
        boolean[] find = new boolean[NUM];

        int vnear = ;

        for (int i = ; i < mindist.length; i++) {
            prenode[i] = i;
            mindist[i] = Graph[vs][i];
            find[i] = false;
        }

        find[vs] = true;

        for (int v = ; v < Graph.length; v++) {

            // 每次循环求得距离vs最近的节点vnear和最短距离min
            int min = N;
            for (int j = ; j < Graph.length; j++) {
                if (!find[j] && mindist[j] < min) {
                    min = mindist[j];
                    vnear = j;
                }
            }
            find[vnear] = true;

            // 根据vnear修正vs到其他所有节点的前驱节点及距离
            for (int k = ; k < Graph.length; k++) {
                if (!find[k] && (min + Graph[vnear][k]) < mindist[k]) {
                    prenode[k] = vnear;
                    mindist[k] = min + Graph[vnear][k];
                }
            }
        }

        for (int i = ; i < NUM; i++) {
            System.out.println("v" + vs + "...v" + prenode[i] + "->v" + i + ", s=" + mindist[i]);
        }

        int before=ds;
        int b=;
        String q=null;
        ArrayList<String> array=new ArrayList<String>();//Java数组动态增加容量,采用ArrayList类数组，它可以在需要时自动扩容；
        array.add(String.valueOf(ds));//保存经过的路径节点
        while(true) {
            b=prenode[before];
            if(b==before) {
                  break;
            }
            before=b;
            if(before==vs) {
                q=String.valueOf(before);//int型强转为String类型
                array.add(q);
                break;
            }
            else {
                q=String.valueOf(before);
                array.add(q);
            }

        }
        array.add(String.valueOf(vs));
        System.out.println(array);//输出找到的路径经过的点
    }
}