opencv —— moments 矩的计算（空间矩/几何矩、中心距、归一化中心距、Hu矩）

计算矩的目的

从一幅图像计算出来的矩集，不仅可以描述图像形状的全局特征，而且可以提供大量关于该图像不同的几何特征信息，如大小，位置、方向和形状等。这种描述能力广泛应用于各种图像处理、计算机视觉和机器人技术领域的目标识别与方位估计中。同时矩函数在图像分析中也有着广泛的应用，如模式识别、目标分类、目标识别与方位估计、图像的编码与重构等。

矩的计算：moments 函数

moments 函数可以很方便的计算出多边形区域的最高三阶空间矩，中心矩和归一化中心矩。

Moments moments(InputArray array, bool binnaryImage = false);

• array，一幅 8 位、单通道图像，或一个二维浮点数组(Point of Point2f)。
• binnaryImage，是否为二值图像。默认为 false。若此值为 true，则所有非零像素均为 1，需注意的是，此参数仅对图像使用。
• 返回值为 Moments 类型对象（矩）

几种常见矩：空间矩/几何矩、中心距、归一化中心距、Hu矩

空间矩/几何矩

空间矩的实质为面积或者质量。可以通过一阶矩计算质心/重心。

空间矩计算公式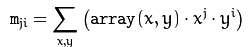：  其中（i+j）等于几就叫几阶矩。

重心计算公式（中心 centers）：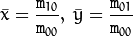

中心距

中心矩体现的是图像强度的最大和最小方向（中心矩可以构建图像的协方差矩阵），其只具有平移不变性，所以用中心矩做匹配效果不会很好。

中心距计算公式：

归一化中心矩

归一化后具有尺度不变性。

归一化中心距计算公式：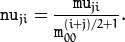

Hu矩

Hu矩具有尺度、旋转、平移不变性，可以用来做匹配。

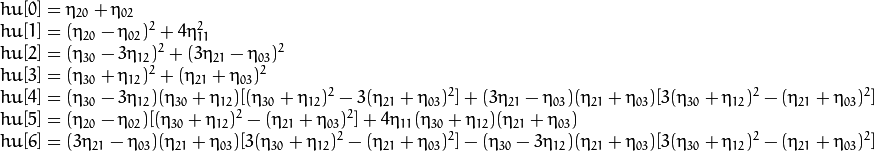
借鉴博客：https://www.cnblogs.com/fcfc940503/p/11319251.html

https://blog.csdn.net/kuweicai/article/details/79027388

https://blog.csdn.net/qq_30815237/article/details/86925736