BP神经网络 详解模板

%原始数据输入
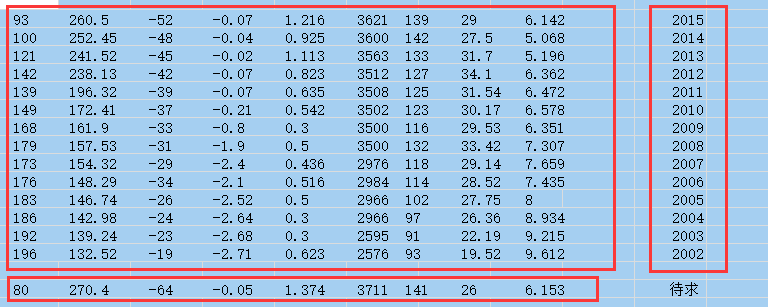
P=[     260.5     -     -0.07    1.216                6.142
       252.45    -     -0.04    0.925          27.5    5.068
       241.52    -     -0.02    1.113          31.7    5.196
       238.13    -     -0.07    0.823          34.1    6.362
       196.32    -     -0.07    0.635          31.54   6.472
       172.41    -     -0.21    0.542          30.17   6.578
       161.9     -     -0.8     0.3            29.53   6.351
       157.53    -     -1.9     0.5            33.42   7.307
       154.32    -     -2.4     0.436          29.14   7.659
       148.29    -     -2.1     0.516          28.52   7.435
       146.74    -     -2.52    0.5            27.75
       142.98    -     -2.64    0.3             26.36   8.934
       139.24    -     -2.68    0.3             22.19   9.215
       132.52    -     -2.71    0.623           19.52   9.612 ]
P=P'    % 保证输入的P是每行对应一个指标
T=[  %期望输出矩阵T

]
T=T'    % 神经网络输出结果为一行
[p1,minp,maxp,t1,mint,maxt]=premnmx(P,T);  %将数据归一化
net=newff(minmax(P),[,,],{'tansig','tansig','purelin'},'trainlm');  %创建网络
net.trainParam.epochs = ;  %训练次数设置
net.trainParam.goal=0.0000001;  %训练所要达到的精度
[net,tr]=train(net,p1,t1);      %训练网络

a=[; 270.4;-;-0.05;1.374;;;;6.153];    %输入数据
a=premnmx(a);    %归一化
b=sim(net,a);    %放入到网络输出数据
c=postmnmx(b,mint,maxt);    % 将得到的数据反归一化得到预测数据
c    建好m文件，运行完事

https://blog.csdn.net/kebu12345678/article/details/80867288  神经网络工具箱使用