MLE
独立同分布的采样x1,x2,…,xn,θ为模型参数,f为我们所使用的模型。参数为θ的模型f产生上述采样可表示为
f(x1,x2,…,xn|θ)=πf(xi|θ)
已知的为x1,x2,…,xn,未知为θ,故似然定义为:L(θ|x1,x2,…,xn)=f(x1,x2,…,xn|θ)=πf(xi|θ)
常用的是两边取对数,得到公式如下:
lnL(θ|x1,x2,…,xn)=Σlnf(xi|θ)
其中lnL(θ|x1,x2,…,xn)称为对数似然,
而
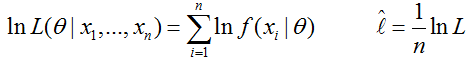
称为平均对数似然。而我们平时所称的最大似然为最大的对数平均似然,即:
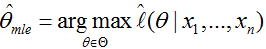
MLE的更多相关文章
- 萌新笔记——Cardinality Estimation算法学习(二)(Linear Counting算法、最大似然估计(MLE))
在上篇,我了解了基数的基本概念,现在进入Linear Counting算法的学习. 理解颇浅,还请大神指点! http://blog.codinglabs.org/articles/algorithm ...
- 最大似然估计 (MLE) 最大后验概率(MAP)
1) 最大似然估计 MLE 给定一堆数据,假如我们知道它是从某一种分布中随机取出来的,可是我们并不知道这个分布具体的参,即"模型已定,参数未知". 例如,我们知道这个分布是正态分布 ...
- 最大似然估计(MLE)与最小二乘估计(LSE)的区别
最大似然估计与最小二乘估计的区别 标签(空格分隔): 概率论与数理统计 最小二乘估计 对于最小二乘估计来说,最合理的参数估计量应该使得模型能最好地拟合样本数据,也就是估计值与观测值之差的平方和最小. ...
- 最大似然估计(MLE)和最大后验概率(MAP)
最大似然估计: 最大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”.简单而言,假设我们要统计全国人口的身高,首先假设这个身高服从服从正态分布,但是该分布的均值与方差未知 ...
- MLE MAP EM
1.最大似然估计 (MLE): 什么是最大似然估计? 问题:给定一组观察数据还有一个参数待定的模型,如何来估计这个未知参数呢? 观察数据(x1,y1)......(xn,yn) 待定模型 ...
- python sklearn PCA源码阅读:参数n_components的设置(设为‘mle’出错的原因)
在介绍n_components参数之前,首先贴一篇PCA参数详解的文章:http://www.cnblogs.com/akrusher/articles/6442549.html. 按照文章中对于n_ ...
- 参数估计:最大似然估计MLE
http://blog.csdn.net/pipisorry/article/details/51461997 最大似然估计MLE 顾名思义,当然是要找到一个参数,使得L最大,为什么要使得它最大呢,因 ...
- 频率学派与贝叶斯学派(先验分布与后验分布,MLE和MAP)
频率学派(古典学派)和贝叶斯学派是数理统计领域的两大流派. 这两大流派对世界的认知有本质的不同:频率学派认为世界是确定的,有一个本体,这个本体的真值是不变的,我们的目标就是要找到这个真值或真值所在的范 ...
- 详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解
转载声明:本文为转载文章,发表于nebulaf91的csdn博客.欢迎转载,但请务必保留本信息,注明文章出处. 原文作者: nebulaf91 原文原始地址:http://blog.csdn.net/ ...
- 补充资料——自己实现极大似然估计(最大似然估计)MLE
这篇文章给了我一个启发,我们可以自己用已知分布的密度函数进行组合,然后构建一个新的密度函数啦,然后用极大似然估计MLE进行估计. 代码和结果演示 代码: #取出MASS包这中的数据 data(geys ...
随机推荐
- ArcGIS for qml -添加自由文本
源码:https://github.com/sueRimn/ArcGIS-for-qml-demos 实现地图上鼠标点击后添加自由文本功能 作者: 狐狸家的鱼 Github: 八至 版权声明:如需转载 ...
- Macbook外接显示器模糊解决方法
解决方法(此方法经本人测试失败) 下载这个http://www.elias.cn/uploads/Mac/patch-edid.zip.如果链接失效可以使用https://gist.github.co ...
- 跟我一起学习vue2(熟悉vue.js)[一]
由于有angularjs的基础,所以我第一步是在官网:https://cn.vuejs.org/ 上面看了三遍他的理论知识,还有实例. 现在做完了第二步,就是在菜鸟教程:http://www.runo ...
- struts2 防止表单的重复提交
防止表单重复提交(拦截器) 1.回顾之前的解决办法: 2.Struts2中的解决办法: 2.1.使用重定向 <result type="redirect">/succe ...
- Day019--Python--反射
1. issubclass, type, isinstance issubclass 判断XXX类是否是XXX类的子类 type 给出XXX的数据类型. 给出创建这个对象的类 isinstance 判 ...
- TestNg 7.依赖测试
我本个测试方法执行的时候,依赖于其他的方法.用到关键字dependsOnmethods(依赖于那个方法)也有依赖于哪个组(dependsOnGroups). 看以下的一段代码: package com ...
- postman charles设置代理
1.首先现在证书 2.确保手机和电脑是同一网络,ifconfig查看电脑ip 3.设置手机->配置代理-手动-服务器(电脑的ip)-端口8888 4.设置charles代理 5.重新启动char ...
- VMware for mac inside error solutions
Terminal 下执行 sudo xattr -r -d com.apple.quarantine /Applications/VMware\ Fusion.app 之后就能正常打开镜像安装虚拟机了 ...
- mysql 将一张表的数据更新到另外一张表中
update 更新表 set 字段 = (select 参考数据 from 参考表 where 参考表.id = 更新表.id); update table_2 m set m.column = ...
- oracle 12C版本的下载安装
首先 去官网下载自己需要的oracle对应的操作系统的版本 接受协议后可下载 1 下载解压好后 进入主目录 进行安装 在配置安全更新中把我希望通过My Oracle Support接收安全更新前面的 ...
