计算机图形学（第2版 于万波 于硕 编著）第45页的Bresenham算法有错误

计算机图形学（第2版 于万波 于硕 编著）第45页的Bresenham算法有错误：

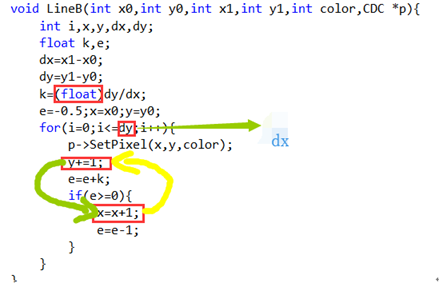
书上本来要写的是以x为阶越步长的方法，但是他写的是用一部分y为阶越步长的方法（其实也写的不对），最后以x为阶越步长的方法总结。

分析书上的算法得：

l  K初始值<=0  画出的是 x=0;

l  0<K初始值<1  画出的是 1/k的直线;

l  K初始值>=1  画出的是 y=x;

以下黑色的线是使用MoveTo，Lineto画出的，红色的是书上的程序画出的，蓝色的线是我修改后的直线（有除法），紫色的是修改后（无除法的）。

绿色的线是验证0<K初始值<1时1/k的直线（使用MoveTo，Lineto画出）

  

(500,-500),(0,0) k=-1        (0,0),(500,500) k=1        (0,0),(400,100) k=1/4

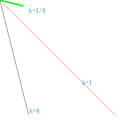
(0,0),(100,400) k=4

修改后得：（主要展示0<=k<=1）

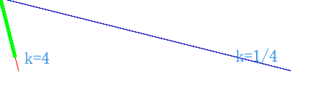
(0,0),(400,100) k=1/4(有乘法)

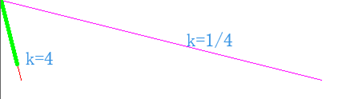
(0,0),(400,100) k=1/4(无乘法)

无乘法程序：