numpy学习之前的必要数学知识:线性代数

行列式

主要内容

1.行列式的定义及性质

2.行列式的展开公式

一.行列式的定义

1.排列和逆序

排列:由n个数1,2,…,n组成的一个有序数组称为一个n级排列,n级排列共有n!个

逆序:在一个排列中,如果一个大的数排在了一个小的数前面,就称这两个数构成了一个逆序

逆序数:在一个排列i1,i2,…,in中,逆序的总数称为该排列的逆序数,记为τ(i1i2…in)

如τ(32514)=5

2.行列式的定义

注：对于行列式的定义把握以下两点

1、 n阶行列式每一项是取自不同行，不同列的n个元素的乘积，共有n！项

2、 当行下标顺排时，每一项的正负号由列下标j1j2…jn的逆序数决定τ(j1j2…jn)

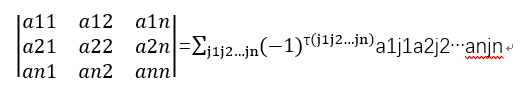
二.行列式的性质

性质1:行列互换,其值不变

性质2:两行(列)互换,行列式的值变号

性质3:两行(列)相同,行行列式的值为0

性质3:某行(列)有公因子k,则可把k提到行列式外

特别地:

1.某行(列)全为0,行列式的值为0

2.某行(列)元素对应成比例,行列式的值为0

性质4:某行(列)是两个元素之和,则可拆成两个行列式之和

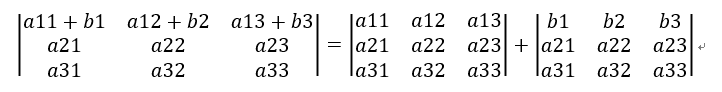
性质5:某行(列)元素的k倍加到外一行(列)对应元素上,行列式的值不变

三.行列式的展开公式

1.余子式

在行列式中,去掉元素aij所在地i行,第j列元素,由剩余的元素按照原来的位置与顺序组成的n-1阶行列式称为元素aij的余子式记为Mij

2.代数余子式称

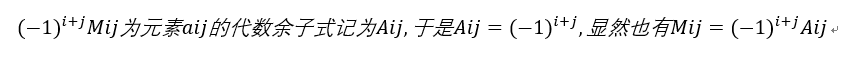
3.行列式按行(列)展开公式

行列式的值等于它的任一行(列)元素与其对应的代数余子式乘积之和

四.几个重要的行列式

1.上(下)三角行列式

2.关于副对角线行列式

3.两个特殊的拉普拉斯展开式

4.范德蒙行列式

计算数值型行列式

基本思想:利用行列式的性质恒等变形,以期望出现尽可能多的0元素,再使用展开式公式,另外也需要灵活应用上面几个重要的展开式

矩阵及其运算

1.矩阵的基本运算

2.幂,转置,伴随,逆

3.初等变换与初等矩阵

4.秩

一.矩阵的定义

由m n个数,排成的m行n列的表格

若m=n,则称为n阶方阵

若A与B,都是m n的矩阵,则称A与B是同型矩阵

若A与B是同型矩阵且对应元素aij=bij,则A=B

特殊的几个矩阵

1.零矩阵,每个元素都是0的矩阵,记为O

2.行向量,只有一行的矩阵称为行矩阵,也叫行向量

3.列向量,只有一列的矩阵称为行矩阵,也叫列向量

4.单位阵,主对角元素均为1,其余元素全为0的n阶方阵

5.数量阵,主对角元素均为k,其余元素全为0的n阶方阵

6.对角阵,主对角以外的元素全为0

7.上(下)三角阵,主对角以下(以上)元素全为0

二.矩阵的基本运算

1.加法运算,同型且对应运算相加

2.数乘运算,数k乘每一个元素

3.乘法运算,A的列等于B的行,且对应元素相乘再相加

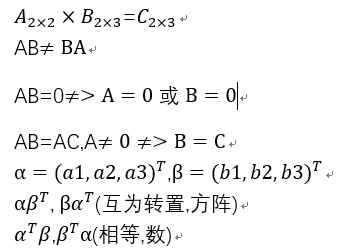
4.方阵的幂

5.转置的运算

6.方阵的行列式

三.伴随矩阵

1.定义

后续更新中.....