用python turtle实现汉诺塔的移动

1.汉诺塔

汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

2.算法介绍

当盘子的个数为n时，移动的次数应等于2^n – 1

后来一位美国学者发现一种出人意料的简单方法，只要轮流进行两步操作就可以了。首先把三根柱子按顺序排成品字型，把所有的圆盘按从大到小的顺序放在柱子A上，根据圆盘的数量确定柱子的排放顺序：若n为偶数，按顺时针方向依次摆放 A B C；

若n为奇数，按顺时针方向依次摆放 A C B。

⑴按顺时针方向把圆盘1从现在的柱子移动到下一根柱子，即当n为偶数时，若圆盘1在柱子A，则把它移动到B；若圆盘1在柱子B，则把它移动到C；若圆盘1在柱子C，则把它移动到A。

⑵接着，把另外两根柱子上可以移动的圆盘移动到新的柱子上。即把非空柱子上的圆盘移动到空柱子上，当两根柱子都非空时，移动较小的圆盘。这一步没有明确规定移动哪个圆盘，你可能以为会有多种可能性，其实不然，可实施的行动是唯一的。

⑶反复进行⑴⑵操作，最后就能按规定完成汉诺塔的移动。

所以结果非常简单，就是按照移动规则向一个方向移动金片：

如3阶汉诺塔的移动：A→C,A→B,C→B,A→C,B→A,B→C,A→C

 

3.过程进行

用python进行汉诺塔的计算：

其代码为：

def hanoi(n, a, b, c):
    if n == :
        print(a, '-->', c)
    else:
        hanoi(n - , a, c, b)
        print(a, '-->', c)
        hanoi(n - , b, a, c)
# 调用
hanoi(, 'A', 'B', 'C')

其结果为：

但是为了更好地看出汉诺塔的移动过程，我利用了python中的turtle进行绘制

代码如下：

def creat_plates(n):#制造n个盘子
    plates=[turtle.Turtle() for i in range(n)]
    for i in range(n):
        plates[i].up()
        plates[i].hideturtle()
        plates[i].shape("square")
        plates[i].shapesize(,-i)
        plates[i].goto(-,-+*i)
        plates[i].showturtle()
    return plates

def pole_stack():#制造poles的栈
    poles=[Stack() for i in range()]
    return poles

def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
    mov=poles[fp].peek()
    plates[mov].goto((fp-)*,)
    plates[mov].goto((tp-)*,)
    l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
    plates[mov].goto((tp-)*,-+*l)

def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
    if height >= :
        moveTower(plates,poles,height-,fromPole,withPole,toPole)
        moveDisk(plates,poles,fromPole,toPole)
        poles[toPole].push(poles[fromPole].pop())
        moveTower(plates,poles,height-,withPole,toPole,fromPole)

myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
    poles[].push(i)
moveTower(plates,poles,n,,,)
myscreen.exitonclick()

输入5结果显示如下：

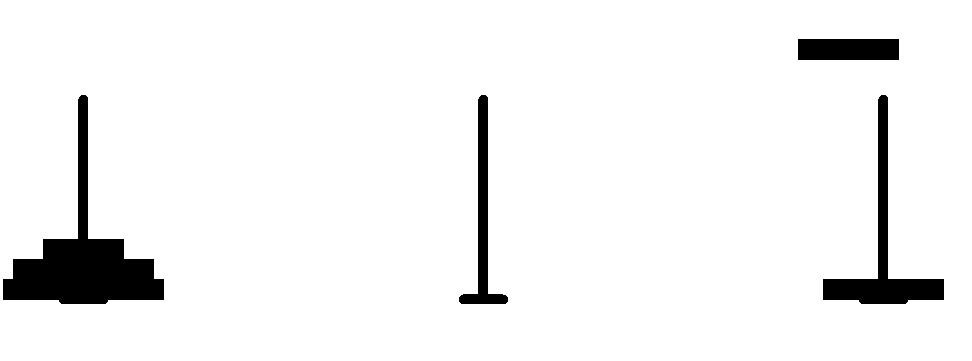
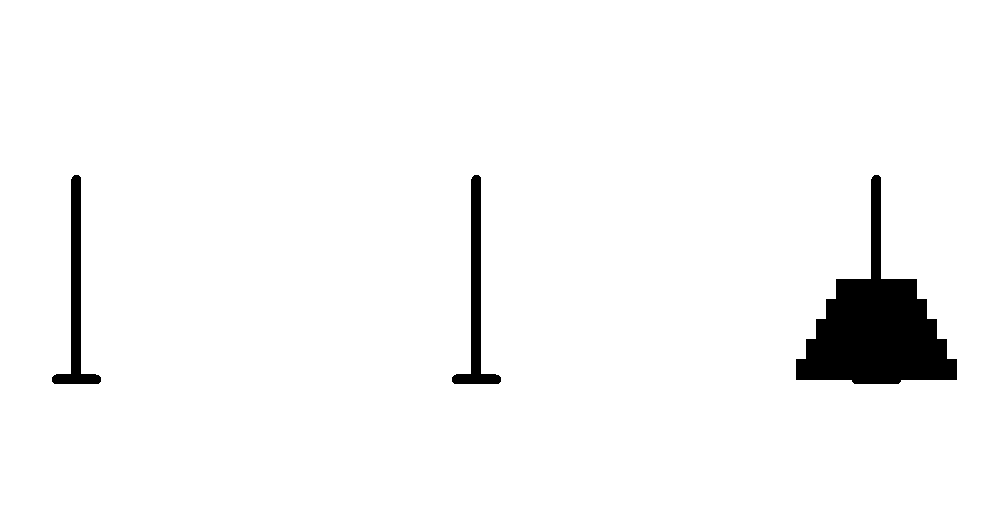
由于不能显示移动图，只能用几张图来显示