洛谷P1224 向量内积

什么毒瘤......

题意：给定n个d维向量，定义向量a和b的内积为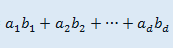

求是否存在两个向量使得它们的内积为k的倍数，并给出任一种方案。k <= 3。

解：很容易想到一个暴力是n²d的。显然我们不能n²枚举，所以要一次性把一个向量跟多个向量判断。

先思考k = 2的情况，显然每个位置和内积非0即1，这启发我们使用二进制。

假如把一个内积看成一个B进制数或者一个多项式，变量是B，我们就能发现，如果两个向量的内积为x，那么这个多项式的值也是x。

这种情况只要B取一个奇数就行了。理由是内积每一项非0即1，而进制为奇数的话，每一项的xⁱ % 2 = 1，奇偶性不变。所以最后加起来和直接加起来的奇偶性相同。

k = 3的时候只要进制为3a + 1就行了。所以最终我们选择7进制。

然后有个很严峻的问题：我们要找一个运算使之与按位乘相对应。先想到了转成指标加法，经过一番推倒之后发现不可行。然后陷入江局......

正解：再观察一波内积式子，您就会发现这个其实是矩阵乘法中的一个位置的计算式......反正我是没发现。

那么令A = n × d的矩阵，B = A * A^T，则B_i,j就是i和j的内积。

然后我们只需检验B和全1矩阵(对角线不一定是1)是否相同即可。这有一个经典算法：随机向量法。

随机出来的向量哪一位不同，就表明在全1矩阵的哪一列中存在差异。枚举跟这个向量匹配的向量即可。

k = 3的时候，我们把B中每一个元素都取平方，这样1和2都会变成1。

那么怎么把B中的每个元素取平方呢？

把B中某个元素的式子化开，会有：

然后就做完了......

 #include <cstdio>
 #include <algorithm>
 #include <ctime>
 #include <iostream>
 
 const int N = ;
 
 int a[N][], now[N], C[N], D[N], E[N], MO, F[N];
 int n, d;
 
 inline bool check(int i, int j) {
     int ans = ;
     for(int k = ; k <= d; k++) {
         (ans += a[i][k] * a[j][k]) %= MO;
     }
     return ans;
 }
 
 inline void solve1() {
     int T = , f = -;
     while((T--) && (f == -)) {
         int Sum = ;
         for(int i = ; i <= n; i++) {
             C[i] = rand() & ;
             Sum += C[i];
         }
         //mul(1, n, d, C, a, D);
         for(int i = ; i <= d; i++) {
             D[i] = ;
             for(int j = ; j <= n; j++) {
                 D[i] += C[j] * a[j][i];
                 D[i] &= ;
             }
         }
         //mul(1, d, n, D, aT, E);
         for(int i = ; i <= n; i++) {
             E[i] = ;
             for(int j = ; j <= d; j++) {
                 E[i] += D[j] * a[i][j];
                 E[i] &= ;
             }
         }
         //mul_one(1, n, n, C, F);
         for(int i = ; i <= n; i++) {
             F[i] = ((Sum - C[i]) + C[i] * now[i]) & ;
             if(E[i] != F[i]) {
                 f = i;
                 break;
             }
         }
     }
     if(f == -) {
         printf("%d %d\n", f, f);
         return;
     }
     for(int i = ; i <= n; i++) {
         if(i == f) {
             continue;
         }
         if(!check(i, f)) {
             printf("%d %d\n", std::min(i, f), std::max(i, f));
             return;
         }
     }
     return;
 }
 
 inline void solve2() {
     int T = , f = -;
     while((T--) && (f == -)) {
         int Sum = ;
         for(int i = ; i <= n; i++) {
             C[i] = rand() % MO;
             Sum += C[i];
         }
         //mul(1, n, d, C, a, D);
         for(int i = ; i <= d; i++) {
             for(int ii = ; ii <= d; ii++) {
                 int pos = (i - ) * d + ii;
                 D[pos] = ;
                 for(int j = ; j <= n; j++) {
                     D[pos] += C[j] * a[j][i] * a[j][ii];
                     D[pos] %= MO;
                 }
             }
         }
         //mul(1, d, n, D, aT, E);
         for(int i = ; i <= n; i++) {
             E[i] = ;
             for(int j = ; j <= d; j++) {
                 for(int jj = ; jj <= d; jj++) {
                     int pos = (j - ) * d + jj;
                     E[i] += D[pos] * a[i][j] * a[i][jj];
                     E[i] %= MO;
                 }
             }
         }
         //mul_one(1, n, n, C, F);
         for(int i = ; i <= n; i++) {
             F[i] = ((Sum - C[i]) + C[i] * now[i]) % MO;
             if(E[i] != F[i]) {
                 f = i;
                 break;
             }
         }
     }
     if(f == -) {
         printf("%d %d\n", f, f);
         return;
     }
     for(int i = ; i <= n; i++) {
         if(i == f) {
             continue;
         }
         if(!check(i, f)) {
             printf("%d %d\n", std::min(i, f), std::max(i, f));
             break;
         }
     }
     return;
 }
 
 int main() {
     srand(time());
     int k, x;
     scanf("%d%d%d", &n, &d, &k);
     MO = k;
     bool f = (k == );
     for(int i = ; i <= n; i++) {
         now[i] = ;
         for(int j = ; j <= d; j++) {
             scanf("%d", &x);
             a[i][j] = x % k;
             now[i] += a[i][j] * a[i][j];
         }
         now[i] %= k;
     }
 
     f ? solve1() : solve2();
     return ;
 }

AC代码

题解里还有一种神奇的解法，使用了乘法分配率，每次把一个向量和它上面所有向量的乘积加起来跟(i-1) % MO判断。

分配一下，就是把上面向量的每一维都做前缀和，然后相乘。

这样做其实有一点问题，就是可能有乘积为0的检测不出来。不过上面那种方法也彼此彼此了。