【数模】day06-数理统计I

数理统计。

以样本推断总体，进而用总体研究问题。

分两部分学习，第一部分是基础统计、参数估计、假设检验以及bootstrap方法。

1. 基础统计

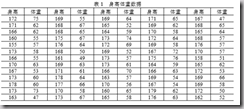
假设有如下数据：

要做频数表、直方图、折线图、饼状图等等，首先要做的是如何把这些数据在matlab中表示。

先把数据写入一个纯文本数据文件 data.txt 中， 格式如上表，有 20 行、10 列，数据列之间用空格键或 Tab 键分割，该数据文件 data.txt 存放在 matlab\work 子目录下，在 Matlab 中用 load 命令读入数据，具体作法是：

load data.txt

这样在内存中建立了一个变量 data，它是一个包含有 10 20× 个数据的矩阵。 为了得到我们需要的 100 个身高和体重各为一列的矩阵，应做如下的改变：

high=data(:,1:2:9);high=high(:)

weight=data(:,2:2:10);weight=weight(:)

接着做频数以及直方图：

求频数用 hist 命令实现，其用法是：

[N,X] = hist(Y,M)

得到数组（行、列均可）Y 的频数表。它将区间[min(Y),max(Y)]等分为 M 份（缺省时 M 设定为 10），N 返回 M 个小区间的频数，X 返回 M 个小区间的中点。

命令 hist(Y,M) 画出数组 Y 的直方图。

Matlab 中 moment(x,order)返回 x 的 order 阶中心矩，order 为中心矩的阶数。 skewness(x)返回 x 的偏度，kurtosis(x)返回峰度。

Matlab 统计工具箱中有 27 种概率分布，这里只对上面所述 4 种分布列出命令的字 符：

norm  正态分布；

chi2   卡方分布；

t      t分布

f    F 分布

工具箱对每一种分布都提供 5 类函数，其命令的字符是：

pdf 概率密度；

cdf 分布函数；

inv 分布函数的反函数；

stat 均值与方差；

rnd 随机数生成：符合该分布的随机数

当需要一种分布的某一类函数时，将以上所列的分布命令字符与函数命令字符接起 来，并输入自变量（可以是标量、数组或矩阵）和参数就行了，如：

p=normpdf(x,mu,sigma)  均值 mu、标准差 sigma 的正态分布在 x 的密度函数 (mu=0，sigma=1 时可缺省)。

p=tcdf(x,n)  t分布（自由度 n）在 x 的分布函数。

x=chi2inv(p,n)  卡方分布（自由度 n）使分布函数 F(x)=p 的 x(即 p 分位数)。

[m,v]=fstat(n1,n2)  F 分布（自由度 n1,n2）的均值 m 和方差 v。

几个分布的密度函数图形就可以用这些命令作出，如：

x=-6:0.01:6;y=normpdf(x);z=normpdf(x,0,2);

plot(x,y,x,z),gtext('N(0,1)'),gtext('N(0,2^2)')

2. 参数估计

常见的是点估计和区间估计。

点估计有矩估计（基于大数定律）和最大似然估计（基于贝叶斯公式）。

区间估计常见的是利用α分位点借助常见分布、利用bootstrap区间估计等。

这些理论是数理统计一课的讲授重点。

☆参数估计的 Matlab 实现

对于正态总体：[mu,sigma,muci,sigmaci]=normfit(x,alpha)

其中 x 为样本（数组或矩阵），alpha 为显著性水平 α （alpha 缺省时设定为 0.05），返 回总体均值 μ 和标准差 σ 的点估计 mu 和 sigma，及总体均值 μ 和标准差 σ 的区间估计 muci 和 sigmaci。当 x 为矩阵时，x 的每一列作为一个样本。

Matlab 统计工具箱中还提供了一些具有特定分布总体的区间估计的命令，如 expfit，poissfit，gamfit。

3. 假设检验

对于假设的检验，通常检验分为下面几种：

检验参数（双边、左边、右边）。

检验分布。（分布拟合检验）

检验两个变量是否是同一分布。（秩和检验）

参数检验：

对于正态总体：

在 Matlab 中Z 检验法由函数 ztest 来实现，命令为

[h,p,ci]=ztest(x,mu,sigma,alpha,tail)

在 Matlab 中t检验法由函数 ttest 来实现，命令为

[h,p,ci]=ttest(x,mu,alpha,tail)

还可以用t检验法检验具有相同方差的 2 个正态总体均值差的假设。在 Matlab 中 由函数 ttest2 实现，命令为：

[h,p,ci]=ttest2(x,y,alpha,tail)

与上面的 ttest 相比，不同处只在于输入的是两个样本 x,y（长度不一定相同）， 而不是一个样本和它的总体均值；tail 的用法与 ttest 相似

分布拟合检验