Tarjan求强连通分量，缩点，割点

Tarjan算法是由美国著名计算机专家发明的，其主要特点就是可以求强连通分量和缩点·割点。

而强联通分量便是在一个图中如果有一个子图，且这个子图中所有的点都可以相互到达，这个子图便是一个强连通分量，并且很显然，这个强连通分量里的任何点组成的集合都可以相互到达，为了方便，我们不叫它们为强连通分量，而割点就是如果把这个点去掉，图就不会联通，同理割边就是把这个边去掉图就不会联通。

---

首先是用tarjan求强连通分量：

其中最重要的两个数组便是dfn和low，分别表示被搜索到的时间戳和在栈中最早的点的次序号。（也可以认为在搜索树中最小的子树根）就像是这个子树的父节点的时间戳，如果它的节点最小这样的话我们就要维护使它成为这个子树的父节点（因为父节点的他的时间戳肯定比他的子树小）。

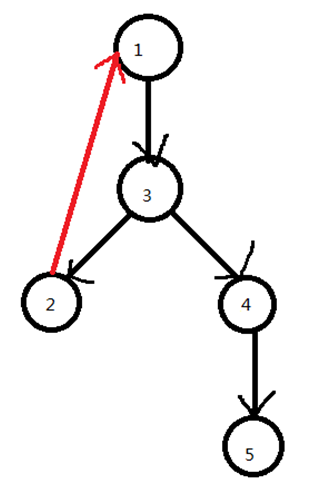
我们将某个图进行一下dfs遍历一下，发现每条边都指向dfn比自己大的边，但是2——1这条边除外，因为就这一个边是一条回边，并且2没有其他的出边,再次搜索到1时dfn[1]==low[1]，那此时1,2,3都在栈中比1相等或靠上的位置，那把1以上的位置的所有点都弹出并记录成一个强连通分量。

我们知道dfn肯定是不变的，但是low可能会改变，当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。(就是这个子树都回溯完了，并且并没有以u为起点的出边了，且他是这个子树中的根节点)所以栈中u以上的点根据深搜性质所有点都是他的子树，那包括他以上的所有点都是一个强连通分量。

由定义可以得出

Low(u)=Min
{
   本身，
   Low(v),//我们将v以u为起点的一条边的终点。如果v这个点并没有搜索过，那我们先把v这个点tarjan一下,然后根据定义更新一下low值.（1）
   DFN(v)//如果v这个点搜索过且这个点在栈中，说明u到v有一条由子节点指向某个祖先的边（2）
 }

有一个对上面三行的解释：

当出现第一种情况时，说明再将v点深搜一遍之后，u的low值是u的low值和v的low值的最小值。

为什么呢，因为v可能会回去，也可能继续向下搜索没有被访问过的点（即dfn还没有确定的点），根据定义，low值一定是最早的点，所以就需要更新。

当出现第二种情况时，说明low[v]还在栈中，且并没有更新，v点的时间戳比现在的时间戳要小，因此也需要进行更新。

上伪代码：

void tarjan(int u)//当前节点
{
    dfn[u]=low[u]=++cnt;//该节点本身是一个强联通分量
    节点入栈;
    vis[u]=true;//当前节点已入栈
    for(遍历该节点所有出边)
    {
        int v=当前边的终点;
        if (!dfn[v])
        {
            tarjan(v);//深度优先遍历
            low[u]=min(low[u],low[v]);
        }
        else low[u]=min(dfn[v],low[u]);
    }
    if (low[u]==dfn[u])
    {
        while(栈顶!=v)
        {
            染色;
            出栈;
        }
    }
    染色;
    出栈;
}

题目（牛的舞会）

这个题是一个裸的求强连通分量的个数的题。

首先我们先建好图，建好图之后我们就可以用Tarjan算法来求强连通分量了，我们先明确好几个变量和他们的用途，最重要的就是dfn和low数组了，结构体e数组是邻接表，point是总的强连通分量的个数，stack是强连通分量的栈，vis是判断是否在栈中，top是栈顶。主函数就不讲了，主要看tarjan函数，首先我们先把每一个点的

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;
],n,m,dfn[],low[],tot,point,cnt,top,stack[],vis[];
struct cym
{
    int from,to,next;
}e[];
void add(int f,int t)
{
    e[++cnt].from=f;
    e[cnt].to=t;
    e[cnt].next=lin[f];
    lin[f]=cnt;
}
void tarjan(int u)
{
    low[u]=dfn[u]=++tot;
    stack[++top]=u;
    vis[u]=;
    for(int i=lin[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(vis[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u])
    {
        ;
        point++;
        ;
        while(v!=u)
        {
            total++;
            v=stack[top--];
            vis[v]=;
        }
        )
        point--;
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    ;i<=m;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v);
    }
    ;i<=n;i++)
        if(!dfn[i])
        tarjan(i);
    printf("%d",point);
    ;
}

会了强联通分量之后还能干什么呢，就可以缩点了，因为一个强联通分量里的点都可以相互到达，所以他们相当于一个点，在DP或搜索的时候，如果题目让你求一个最大值，那我们就可以缩点，因为不走白不走。该怎么缩点呢，我们要把每一个强联通分量里的所有点都染上同一种颜色，然后把每一个强联通分量都变成一个新点，然后建一个新图，然后就由原来的图变成了一个新图。

还可以求割点