1283: 骨牌铺方格（zzuli）

Problem Description

在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数.
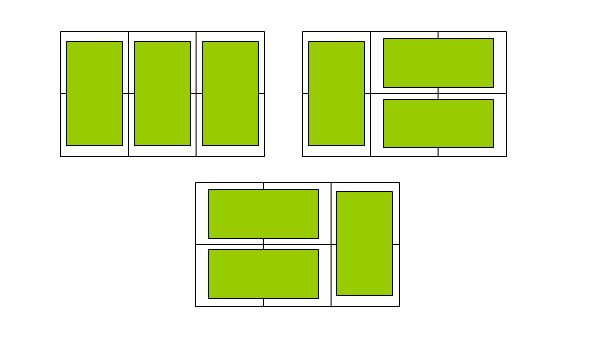
例如n=3时,为2× 3方格，骨牌的铺放方案有三种,如下图：

Input

输入数据由多行组成，每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0<n<=50)。

Output

对于每个测试实例，请输出铺放方案的总数，每个实例的输出占一行。

Sample Input

1 3 2

Sample Output

1 3 2

Author

lcy

Source

递推求解专题练习（For Beginner）

呀，这题的价值蛮不错的，虽然是在看到大佬的题解的情况下写出来的，不过好歹代码是自己写的；

大佬的原话：

只要简单的推断即可~

   假设用arr[i]表示2*i的方格一共有组成的方法数，我们知道arr[1]=1;arr[2]=2;

   现在假设我们已经知道了arr[i-1]和arr[i-2],求arr[i],所谓arr[i],不过是在2*（i-1）的格子后边加上一格2*1的方格罢了，骨牌在这一格上横着放，竖着放，如果前面i-1块已经铺好，则第i块只有一种铺法，就是竖着放，如果要横着放，也只有一种铺法，不过要求前面i-2块已经铺好！

 因此arr[i]=arr[i-1]+arr[i-2];链接：https://blog.csdn.net/enjoying_science/article/details/38535383

 #include<cstdio>
 #include<algorithm>
 #include<map>
 using namespace std;
 int main()
 {
     int n;
     long long s[];
     s[] = , s[] = ;
     for (int i = ; i <= ; i++)
     {
         s[i] = s[i - ] + s[i - ];
     }
     while (~scanf("%d", &n))
     {
         printf("%ld\n", s[n]);
     }
     return ;
 }