用cart（分类回归树）作为弱分类器实现adaboost

在之前的决策树到集成学习里我们说了决策树和集成学习的基本概念（用了adaboost昨晚集成学习的例子），其后我们分别学习了决策树分类原理和adaboost原理和实现，

上两篇我们学习了cart（决策分类树），决策分类树也是决策树的一种，也是很强大的分类器，但是cart的深度太深，我们可以指定cart的深度使得cart变成强一点的弱分类器。

在决策树到集成学习我们提到，单棵复杂的决策树可以达到100%，而简单的集成学习只能有85%的正确率，下面我们尝试用强一点的弱分类器来看下集成学习的效果有没有提升。

首先我们要得到可以指定深度得到一棵cart（到达深度后直接多数表决，返回生成的cart）

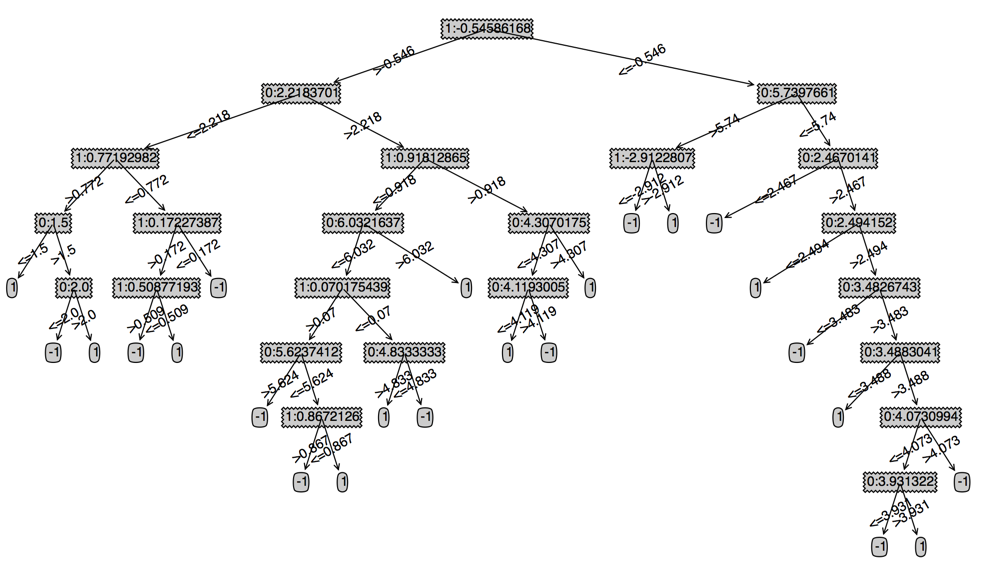
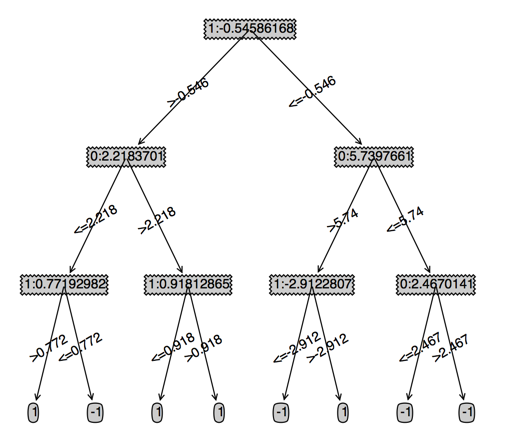
上两篇我们只是学习了cart的原理和实现，我们这里还需要实现如果用cart做预测，为了方便做预测，我们保存cart的时候，节点不在用特征的名称（例如这里的x，y），而是统一改成特征的下标，从0开始，并且节点加上了当前分支的阀值，例如下面的cart（当然，我们可以在最后画图的时候在特征名称转换过来）

下图左边是原始的cart，右边是指定深度的cart

我们重新回顾一下adaboost的整体流程：

1. 对数据集找到最优的弱分类器
2. 用最优的分类器预测，记录预测结果，并相应修改样本的权重
3. 重复上面两个步骤直到错误率为零或者到达最大的迭代次数

如何结合cart和adaboost呢？

cart采用的是gini系数来选择二分特征，而adaboost是通过改变样本的权重来实现弱分类器的迭代，如何将adaboost的改变样本权重的思想融合到cart中去呢？

尝试采用重复样本的方法提高样本的权重

下面直接看实现的代码吧，我觉得我的注释应该够详细了

# cart_adaboost.py
# coding:utf8
from itertools import *
import operator,time,math
import matplotlib.pyplot as plt
def calGini(dataSet):#计算一个数据集的gini系数
    numEntries = len(dataSet)
    labelCounts={}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    gini=1
    for label in labelCounts.keys():
        prop=float(labelCounts[label])/numEntries
        gini -=prop*prop
    return gini

def splitDataSet(dataSet, axis, value,threshold):#根据特征、特征值和方向划分数据集
    retDataSet = []
    if threshold == 'lt':
        for featVec in dataSet:
            if featVec[axis] <= value:
                retDataSet.append(featVec)
    else:
        for featVec in dataSet:
            if featVec[axis] > value:
                retDataSet.append(featVec)

    return retDataSet
# 由于是连续值，如果还是两两组合的话，肯定爆炸
# 并且连续值根本不需要组合，只需要给定值，就可以从这个分开两份
# 返回最好的特征以及特征值
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1
    bestGiniGain = 1.0; bestFeature = -1;bsetValue=""
    for i in range(numFeatures):        #遍历特征
        featList = [example[i] for example in dataSet]#得到特征列
        uniqueVals = list(set(featList))       #从特征列获取该特征的特征值的set集合
        uniqueVals.sort()
        for value in uniqueVals:# 遍历所有的特征值
            GiniGain = 0.0
            # 左增益
            left_subDataSet = splitDataSet(dataSet, i, value,'lt')
            left_prob = len(left_subDataSet)/float(len(dataSet))
            GiniGain += left_prob * calGini(left_subDataSet)
            # 右增益
            right_subDataSet = splitDataSet(dataSet, i, value,'gt')
            right_prob = len(right_subDataSet)/float(len(dataSet))
            GiniGain += right_prob * calGini(right_subDataSet)
            # print GiniGain
            if (GiniGain < bestGiniGain):      #比较是否是最好的结果
                bestGiniGain = GiniGain      #记录最好的结果和最好的特征
                bestFeature = i
                bsetValue=value
    return bestFeature,bsetValue                  

def majorityCnt(classList):#多数表决
    classCount={}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

# 这里用做生成弱分类器的cart
def createTree(dataSet,depth=3):#生成一棵指定深度的cart
    classList = [example[-1] for example in dataSet]
    if depth==0:#如果到达指定深度，直接多数表决
        return majorityCnt(classList)
    if classList.count(classList[0]) == len(classList):
        return classList[0]#所有的类别都一样，就不用再划分了
    if len(dataSet) == 1: #如果没有继续可以划分的特征，就多数表决决定分支的类别
        return majorityCnt(classList)
    bestFeat,bsetValue = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel=str(bestFeat)+":"+str(bsetValue)#用最优特征+阀值作为节点，方便后期预测
    if bestFeat==-1:
        return majorityCnt(classList)
    myTree = {bestFeatLabel:{}}
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = list(set(featValues))
    # print bsetValue
    myTree[bestFeatLabel]['<='+str(round(float(bsetValue),3))] = createTree(splitDataSet(dataSet, bestFeat, bsetValue,'lt'),depth-1)
    myTree[bestFeatLabel]['>'+str(round(float(bsetValue),3))] = createTree(splitDataSet(dataSet, bestFeat, bsetValue,'gt'),depth-1)
    return myTree  

def translateTree(tree,labels):
    if type(tree) is not dict:
        return tree
    root=tree.keys()[0]
    feature,threshold=root.split(":")#取出根节点，得到最优特征和阀值
    feature=int(feature)
    myTree={labels[feature]:{}}
    for key in tree[root].keys():
        myTree[labels[feature]][key]=translateTree(tree[root][key], labels)
    return myTree
def predict(tree,sample):
    if type(tree) is not dict:
        return tree
    root=tree.keys()[0]
    feature,threshold=root.split(":")#取出根节点，得到最优特征和阀值
    feature=int(feature)
    threshold=float(threshold)
    if sample[feature]>threshold:#递归预测
        return predict(tree[root]['>'+str(round(float(threshold),3))], sample)
    else:
        return predict(tree[root]['<='+str(round(float(threshold),3))], sample)

#用cart对数据集做预测，
def cartClassify(dataMatrix,tree):
    errorList=ones((shape(dataMatrix)[0],1))# 返回预测对或者错，而不是返回预测的结果(对为0，错为1，方便计算预测错误的个数)
    predictResult=[]#记录预测的结果
    classList = [example[-1] for example in dataSet]
    for i in range(len(dataMatrix)):
        res=predict(tree,dataMatrix[i])
        errorList[i]=res!=classList[i]
        predictResult.append([int(res)] )
        # print predict(tree,dataMatrix[i]),classList[i]
    return errorList,predictResult

#记录弱分类器，主要调整样本的个数来达到调整样本权重的目的，训练弱分类器由createTree函数生成
def weekCartClass(dataSet,weiths,depth=3):
    min_weights = weiths.min()#记录最小权重
    newDataSet=[]
    for i in range(len(dataSet)):#最小权重样本数为1，权重大的样本对应重复math.ceil(float(array(weiths.T)[0][i]/min_weights))次
        newDataSet.extend([dataSet[i]]*int(math.ceil(float(array(weiths.T)[0][i]/min_weights))))
    bestWeekClass={}
    dataMatrix=mat(dataSet);
    m,n = shape(dataMatrix)
    bestClasEst = mat(zeros((m,1)))
    weekCartTree = createTree(newDataSet,depth)
    errorList,predictResult=cartClassify(dataSet, weekCartTree)
    weightedError = weiths.T*errorList#记录分错的权重之和
    bestWeekClass['cart']=weekCartTree
    return bestWeekClass,predictResult,weightedError

def CartAdaboostTrain(dataSet,num=1,depth=3):
    weekCartClassList=[]
    classList = mat([int(example[-1]) for example in dataSet])
    m=len(dataSet)
    weiths=mat(ones((m,1))/m) #初始化所有样本的权重为1/m
    finallyPredictResult = mat(zeros((m,1)))
    for i in range(num):
        bestWeekClass,bestPredictValue,error=weekCartClass(dataSet,weiths,depth)#得到当前最优的弱分类器
        alpha = float(0.5*log((1.0-error)/max(error,1e-16)))#根据error计算alpha
        bestWeekClass['alpha'] = alpha
        expon = multiply(-1*alpha*mat(classList).T,bestPredictValue)
        weiths = multiply(weiths,exp(expon))
        weiths = weiths/weiths.sum()
        finallyPredictResult += alpha*mat(bestPredictValue)
        nowPredictError = multiply(sign(finallyPredictResult) != mat(classList).T,ones((m,1)))
        errorRate = nowPredictError.sum()/m
        print "total error: ",errorRate
        bestWeekClass['error_rate']=errorRate
        weekCartClassList.append(bestWeekClass)
        if errorRate == 0.0: break
    return weekCartClassList, finallyPredictResult

from treePlotter import createPlot
import numpy as np
from numpy import *
filename="sample"
dataSet=[];labels=[];
with open(filename) as f:
    for line in f:
        fields=line.strip("\n").split("\t")
        t=[float(item) for item in fields[0:-1]]
        t.append(int(fields[-1]))
        dataSet.append(t)
labels=['x','y']
weekCartClass, finallyPredictResult=CartAdaboostTrain(dataSet,10,4)
print finallyPredictResult.T

下面我们看下实验的结果

由于完整的cart有8层，所以CartAdaboostTrain(dataSet,10,8)，只需要一颗cart就可以100%的正确率

cart深度改为7，需要三棵cart

total error: 0.01
total error: 0.01
total error: 0.0

cart改为6，也是三棵cart，但是我们可以发现只有一棵cart的时候正确率是98%

total error:  0.02
total error:  0.02
total error:  0.0

cart改为5，同样也是三棵cart，但是我们可以发现只有一棵cart的时候正确率是95%

total error:  0.05
total error:  0.07
total error:  0.0

cart改为4，这个时候需要5棵cart，同时我们可以发现只有一棵cart的时候正确率只有90%

total error:  0.1
total error:  0.1
total error:  0.06
total error:  0.05
total error:  0.0

cart改为3，居然发现10棵cart还不行，居然需要12棵cart了，一开始的正确也只有89%

total error:  0.11
total error:  0.11
total error:  0.11
total error:  0.06
total error:  0.1
total error:  0.06
total error:  0.03
total error:  0.04
total error:  0.01
total error:  0.02
total error:  0.04
total error:  0.0

cart改为2时，cart的棵数到到了53棵才能达到100%的正确性,一开始的正确也只有86%

而cart改为1成为决策树墩的时候，用了200棵cart才达到95%的正确率

到这里我们可以说成功了实现了使用指定深度的cart作为弱分类器的可以调整cart深度和迭代次数的adaboost算法。

最后我们看下cart深度为3时，每棵cart的权重alpha值以及每个样本最后被预测的值，可以发现最后的预测值不是直接的-1和1，而是差异很大的一些值，这也算是集成学习和单纯决策树的一个区别吧

1.05 0.43 0.54 0.6 0.57 0.68 0.57 0.71 0.66 0.33 0.59 0.53

[-4.22, -2.86, -4.22, -4.22, -4.22, -4.22, -3.97, -6.19, -6.19, -6.19, -5.1, -5.1, -5.1, -3.97, -3.97, -2.6, -1.46, -2.6, -2.82, -2.6, -2.0, -2.0, -2.0, -2.0, -2.0, -3.04, -2.75, -0.95, -2.75, -2.86, -2.86, -4.17, -2.86, -4.22, -4.22, -1.16, -0.98, -1.03, -2.82, -3.97, -2.0, -1.53, -0.85, -1.98, -1.16, -0.85, -0.85, -1.63, -0.99, -1.53, 4.25, 3.92, 2.89, 2.89, 2.64, 3.95, 3.95, 4.98, 4.47, 4.47, 4.47, 4.8, 4.47, 6.19, 6.19, 6.19, 5.1, 6.19, 1.45, 2.43, 4.8, 3.38, 1.45, 5.34, 4.15, 4.47, 1.58, 4.25, 2.56, 3.62, 3.62, 2.56, 4.98, 0.38, 0.51, 4.12, 2.64, 2.43, 4.47, 4.47, 4.47, 2.81, 0.38, 0.51, 1.45, 2.43, 3.83, 2.58, 4.17, -0.77]