Java实现构造无向图的欧拉回路（ The Necklace）

中文翻译：

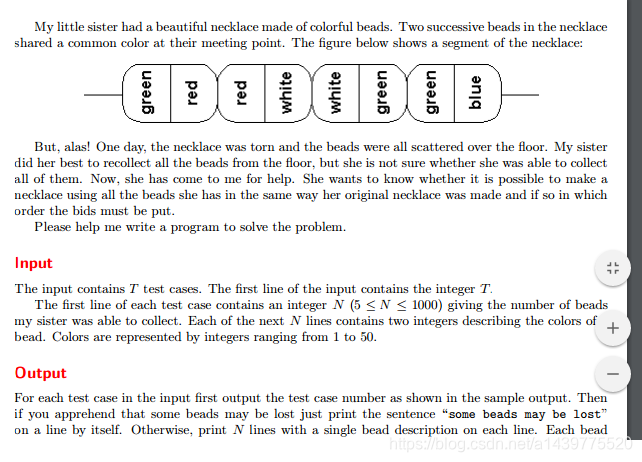
但是，唉！一天，项链被撕破了，珠子散落在屋檐上。我姐姐尽力把地板上的珠子都捡起来了。但她不确定自己是否能收集到所有的照片。现在，她来找我帮忙。她想知道是否有可能让克劳斯使用她在里面的所有珠子，请帮助我写一个程序来解决这个问题。输入这个输入包含t’测试用例。输入的第一行包含整数。bead的数目每个测试用例的第一行包含一个整数n（5<n 1000），因为我妹妹可以收集。接下来的n行中的每一行都包含两个描述珠子颜色的整数。颜色由从1到50的整数表示，对于输入中的每个测试用例，首先输出示例输出中显示的测试用例编号。如果你觉得有些珠子可能会丢失，那就打印出来，这些珠子本身可能会丢失。否则，在每行上打印n行，并使用单珠说明。每个珠在一条线上。否则，在每行上打印n行，并使用单珠说明。每个beadDescription由两个整数组成，给出其两端的颜色。对于1<i<n1，第二行整数i必须与linn上的第一个整数相同，并且必须等于第1行上的第一个整数。由于有许多解决方案，因此其中任何一个都是可接受的，在两个连续的测试用例之间打印一个空白行s25le22356522233示例输出

package com.liuzhen.practice;

import java.util.ArrayList;
import java.util.Scanner;

public class Main {
    public static int MAX = 1000;
    public static int start, count;
    public static int num = 0;
    public static int[] id = new int[MAX];
    public static int[] degree = new int[MAX];  //用于计算给定图每个顶点的度
    public static boolean[] used = new boolean[MAX];   //用于判断图中相应边是否被遍历
    public static String[] path = new String[MAX];
    public static ArrayList<String> result = new ArrayList<String>();                      

    static class edge {
        public int a;  //边的起点
        public int b;  //边的终点
        public int num;  //边的编号

        public edge(int a, int b, int num) {
            this.a = a;
            this.b = b;
            this.num = num;
        }

        public String getAB() {
            return a + " "+ b;
        }
    }
    //寻找顶点a的根节点
    public int find(int[] id, int a) {
        int root = a;
        while(id[root] >= 0) {
            root = id[root];
        }
        int i;
        int k = a;
        while(k != root) {
            i = id[k];
            id[k] = root;
            k = i;
        }
        return root;
    }
    //合并顶点a和顶点b所在的树
    public void union(int[] id, int a, int b) {
        int rootA = find(id, a);
        int rootB = find(id, b);
        if(rootA == rootB)
            return;
        int rootNum = id[rootA] + id[rootB];
        if(id[rootA] < id[rootB]) {
            id[rootB] = rootA;
            id[rootA] = rootNum;
        } else{
            id[rootA] = rootB;
            id[rootB] = rootNum;
        }
        return;
    }

    public void init() {
        count = 0;
        for(int i = 0;i < 51;i++) {
            id[i] = -1;   //初始化所有顶点所在树的根节点编号为-1
            degree[i] = 0;
        }
        for(int i = 0;i < MAX;i++) {
            used[i] = false;
            path[i] = "";
        }
        return;
    }

    public boolean judge(ArrayList<edge>[] map) {
        int root = find(id, start);
        for(int i = 0;i < map.length;i++) {
            for(int j = 0;j < map[i].size();j++) {
                if(root != find(id, map[i].get(j).b))
                    return false;
            }
        }
        for(int i = 0;i < degree.length;i++) {
            if(degree[i] % 2 != 0)
                return false;
        }
        return true;
    }

    public void dfs(ArrayList<edge>[] map, int start) {
        for(int i = 0;i < map[start].size();i++) {
            if(!used[map[start].get(i).num]) {
                used[map[start].get(i).num] = true;
                path[count++] = map[start].get(i).getAB();
                dfs(map, map[start].get(i).b);
            }
        }
    }

    public static void main(String[] args) {
        Main test = new Main();
        Scanner in = new Scanner(System.in);
        int t = in.nextInt();       //总共要输入的图的数目
        while(t > 0) {
            t--;
            @SuppressWarnings("unchecked")
            ArrayList<edge>[] map = new ArrayList[51];
            for(int i = 0;i < 51;i++)
                map[i] = new ArrayList<edge>();
            int k = in.nextInt();   //一次输入图的边数目
            test.init();
            for(int i = 0;i < k;i++) {
                int a = in.nextInt();
                int b = in.nextInt();
                map[a].add(new edge(a, b, num));
                map[b].add(new edge(b, a, num++));
                degree[a]++;
                degree[b]++;
                test.union(id, a, b);
                start = a;
            }
            String temp = "";
            if(test.judge(map)) {
                test.dfs(map, start);
                for(int i = 0;i < k;i++) {
                    temp = temp + path[i] + "\n";
                }
            } else {
                temp = "some beads may be lost";
            }
            result.add(temp);
        }
        for(int i = 0;i < result.size();i++) {
            System.out.println("Case #"+(i+1));
            System.out.println(result.get(i)+"\n");
        }
    }
}

运行结果：

5
2
3
4
5
6
2 1
2
4
1
4
Case #1
some beads may be lost

Case #2
1
3
4
2
2