数据结构——KMP（串）

KMP一个非常经典的字符串模式匹配算法，虽然网上有很多kmp算法的博客，但是为了更好的理解kmp我还是自己写了一遍（这个kmp的字符串存储是基于堆的（heap），和老师说的定长存储略有不同，字符串索引从0开始）

　　先来说说 KMP 的历史吧。

一、背景　　

　　KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度度O(m+n)。KMP也可以处理最重复长子串问题，最长子串问题……这里挂一道最简单的题leetcode的 实现 strStr()，大家看完可以去试一试。

补充说明：

　　强调两个概念：真前缀 ，真后缀　　

如图所示，所谓的真前缀，就是在指在除了自身之外的全部字符串的头部顺序组合；而"真后缀"，就是指在除自身之外的一个字符串的全部尾串的顺序组合 。与后缀、前缀不同：

　　　　　　　　　　　　真前/后缀不包含自身字符！！！

其实就类似于离散数学中集合里子集与真子集的概念。

二、朴素字符串匹配算法

　　其实就是我们最开始的时候写的字符串匹配，就是两个字符串逐一匹配。不作详细介绍，代码如下

/**
 * @brief  朴素字符串匹配
 * @note
 * @param  MainString:  主串
 * @param  Pattern:     模式串
 * @retval
 */
int SimpleStringMatch(char* MainString, char* Pattern)
{
    int i = ;
    int j = ;
    int PatternLen = strlen(Pattern);
    int MainStringLen = strlen(MainString);

    while (i < MainStringLen && j < PatternLen)
    {
        if (S[i] == Pattern[j])
        {
            i++;
            j++;
        }
        else
        {
            i = i - j + ;
            j = ;
        }
    }
    if (j == PatternLen)
    {
        return i - j;
    }
    return -;
}

　　很显然暴力匹配的时间复杂度为O（m*n）。m，n 分别取决于MainString和Pattern的长度，很显然这种时间复杂度还很高的。这个算法一旦匹配失败就主串索引 +1 ，模式串索引重置，当主串为 ABCDEABCDEF 模式串为 ABCDEF 。啊，完美体现了暴力匹配的缺点——逐一匹配（管你之前比没比过）。当你 A ！= F 时，我们人肯定会从第二个A处继续查找，让余下的部分和模式串继续进行匹配。如果计算机这样执行，那么算法的时间复杂度就从O（m*n）降到了O（m+n）从乘数级算法瞬间降到了无限接近常数级的算法，神优化啊（再次膜拜大神）。但是计算机不会啊，他只会勤勤恳恳的执行我们所写的代码，因此它就会从第一个B处开始比较，但是事实上从 B ~ E 的所有匹配都是无用功，为了解决这个问题 KMP应运而生。

三、KMP字符串模式匹配算法

　　3.1 算法流程：

　　（1）

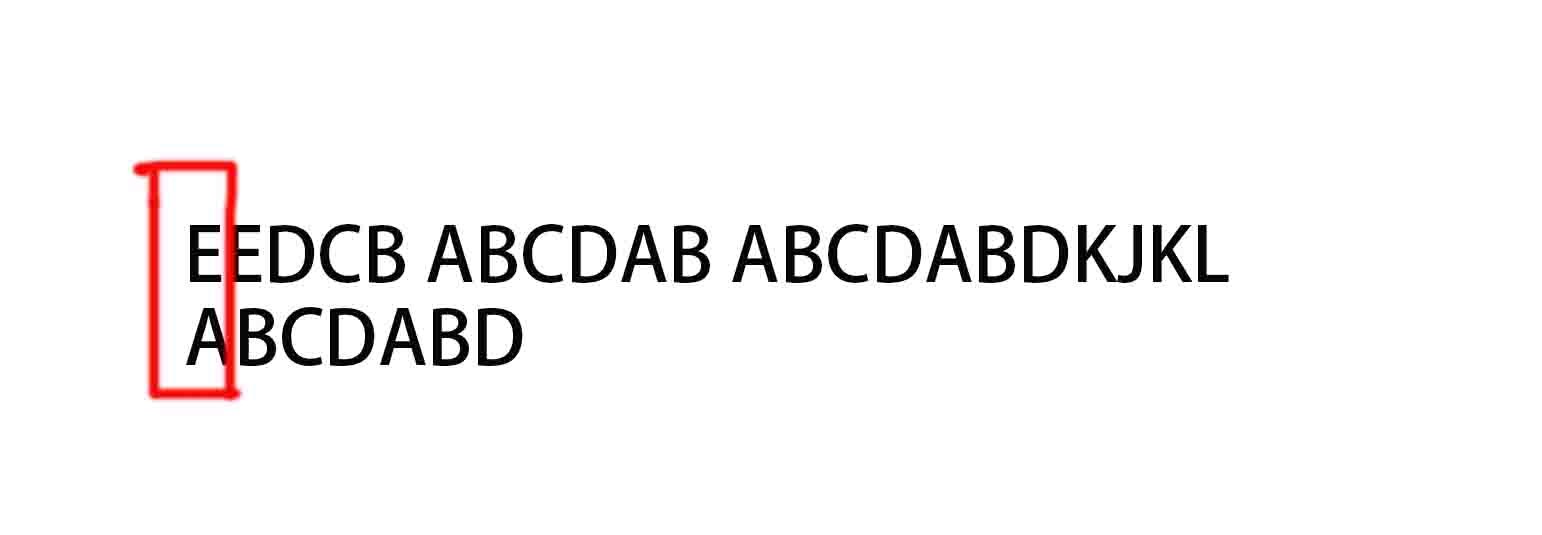
第一步 主串"E……" 与 模式串 "ABCDABD" 的第一个字符进行比较。‘E！= ’A，模式串索引不变，主串索引+1

　　（2）

E与A仍然不匹配，继续后移知道第一个匹配的位置

（3）

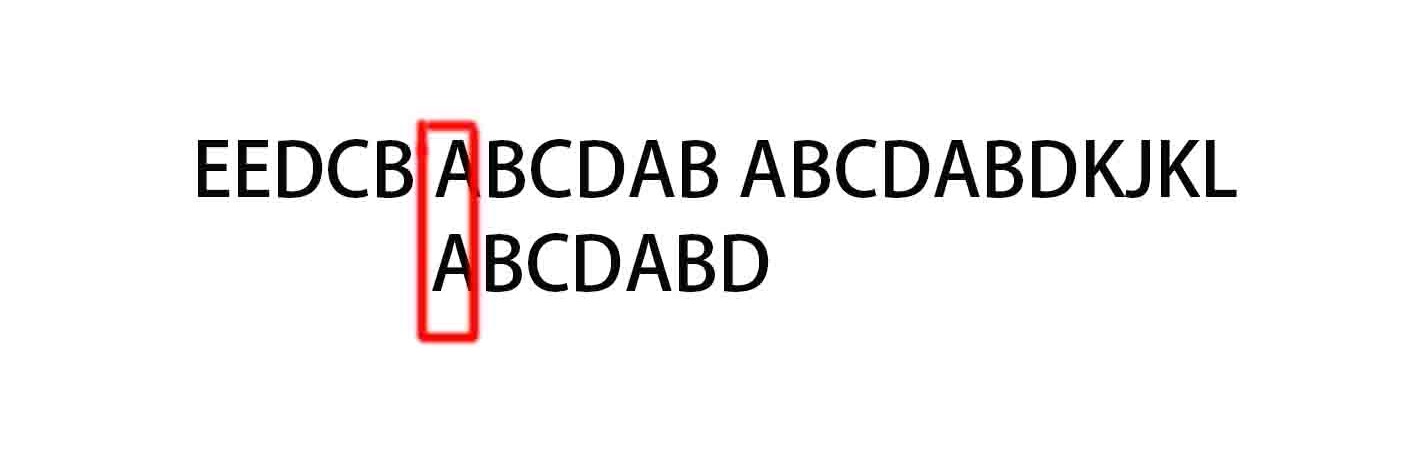
抵达第一处相同点

（4）

第二处相同点，继续

（5）

嗯！，不匹配了，怎么办呢。

（6）

第一反应肯定是把模式串整体后移一位然后重新一位位的比较，这样子是没有问题，但是这就不是kmp了，没有利用已完成的匹配信息。

（7）

当我们发现D和空格不匹配的时候，我们已经知道了前面6个字符为ABCDAB（主串）。KMP就是充分利用了这个信息。将模式串继续后移，没有将其移回比较过的位置。

（8）

计算机不比我们大脑，这种的事情对它来说已经很困难了，肯定要给它写个专门的算法了。KMP的索引的转跳依赖的是next[] 数组。如图，我们先用，先对KMP有一个完整的理解再来进行实现。理解才是关键。

i	0	1	2	3	4	5	6	7
模式串	A	B	C	D	A	B	D	'\0'
next[i]	-1	0	0	0	0	1·	2	0

（9）

如图，D与空格不匹配，D之前的字符已经完成匹配，为已知信息。根据转跳数组可知，不匹配出D的next值为2，因此接下来从模式串所引为2的位置进行匹配。

（10）

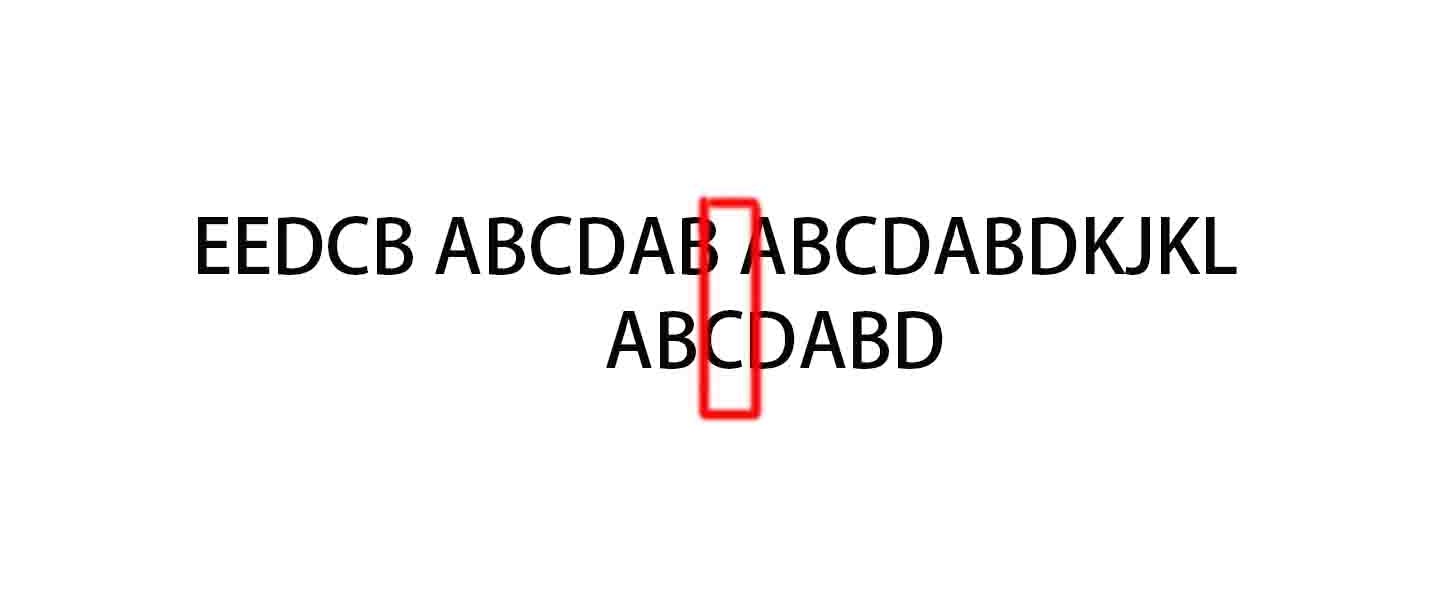
同样的，C与空格不匹配，C处的next为0，所以下一个从索引为0的位置进行匹配。

（11）

A与空格比较不匹配，此处next值为-1，表示模式串的索引为1字符就不匹配，那么直接往后移一位。

（12）

一位位的比较直到完全匹配。

其实KMP的比较算法和朴素匹配的方法是一样的，KMP之所以快是快在索引的转跳上。接着我们就来说一下next数组是u如何实现的。

　　

　　3.2 next数组实现：

next数组的求解基于 "真前缀" 和 "真后缀" ，即next[i]等于P[0]...P[i - 1]最长的相同真前后缀的长度。（忘记的赶紧上去看看，要不然会一直懵的）。

i	0	1	2	3	4	5	6	7
模式串	A	B	C	D	A	B	D	'\0'
next[i]	-1	0	0	0	0	1·	2	0

1. i = 0，对于模式串的首字符，我们统一为next[0] = -1；
2. i = 1，前面的字符串为A，其最长相同真前后缀长度为0，即next[1] = 0；
3. i = 2，前面的字符串为AB，其最长相同真前后缀长度为0，即next[2] = 0；
4. i = 3，前面的字符串为ABC，其最长相同真前后缀长度为0，即next[3] = 0；
5. i = 4，前面的字符串为ABCD，其最长相同真前后缀长度为0，即next[4] = 0；
6. i = 5，前面的字符串为ABCDA，其最长相同真前后缀为字符A，即next[5] = 1；
7. i = 6，前面的字符串为ABCDAB，其最长相同真前后缀为字符AB，即next[6] = 2；
8. i = 7，前面的字符串为ABCDABD，其最长相同真前后缀长度为0，即next[7] = 0。

那么，这个数组是如何实现不匹配自动跳转的呢？

　　举个栗子：前置字符串

　　　　假如 i = 6 时不匹配，其前置字符串为 “ABCDAB”，仔细观察，首尾都有 “AB”，这意味着主串和模式串刚刚比较完 “AB”。那，当进行下一次比较的时候，我们就可以直接用 i = 2 时的字符C进行下一次匹配。因为刚刚模式串后方的“AB”刚比较完，所以没有必要再进行。i =  6 时候字符D的其最长相同真前后缀为字符恰好也为“AB”，长度恰好等于索引，刚好能转跳到C。

但是现在有一个问题，看表中 i = 5 时，匹配失败， next数组值为1，这不符KMP的理念啊。理论上，我们应该把 i = 2 处的字符拿过来匹配，如果拿 i = 1 处的字符那就会产生一次多余的比较。这个问题的遗留并不是算法问题，而是算法没有优化，KMP未优化的算法是用也是有特定作用的。两种算法应用场景不同，各有所长。（最后会说明优化算法的）。

下面是代码实现：

/**
 * @brief  next[]
 * @note   未优化KMP，j == -1 不可删除
 * @param  Pattern: 模式串
 * @param  next[]:  转跳数组
 * @retval None
 */
void GetNext(char* Pattern, int next[])
{
    int Pattern_len = strlen(Pattern);
    int i = ; // Pattern 的下标
    int j = -;
    next[] = -;

    while (i < Pattern_len - )
    {
        if (j == - || Pattern[i] == Pattern[j])
        {
            i++;
            j++;
            next[i] = j;//匹配就递推
        }
        else
        {
            j = next[j];//不匹配就转跳到上一个匹配的位置
        }
    }
}

有没有看懂的，我觉得肯定有。有我也得分析一下这个算法干了什么。

其实，这个代码最难理解的就在于 if……else……

　　先上张图（感谢大佬给我的图）

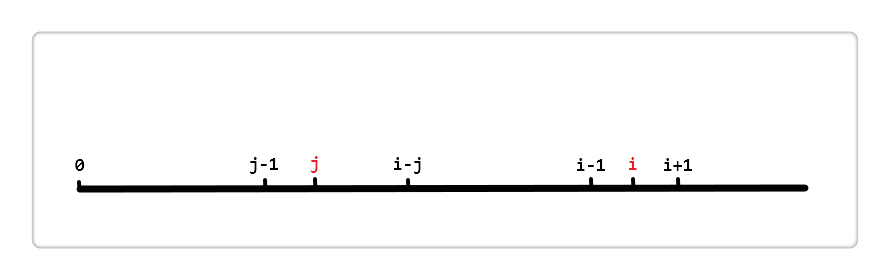
现在我假设 i 和 j 的位置如上，由前面代码中的 next[i] = j 得， i 的最长相同真前后缀分别是 [0, j-1] 和 [i-j, i-1]，即这两段内容相同

走流程：

if (j == - || Pattern[i] == Pattern[j])
{
　　i++;
   j++;
   next[i] = j;
}
else
{
　　j = next[j];
}       

next[j] 表 [0，j - 1] 区间中最长相同真前后缀的长度。如图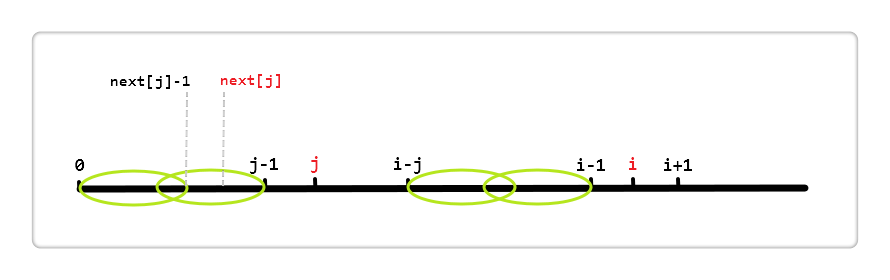

左侧两个椭圆来表示这个最长相同真前后缀，即这两个椭圆代表的区段内容相同；同理，右侧也有相同的两个椭圆。所以else语句就是利用第一个椭圆和第四个椭圆内容相同来加快得到[0, i - 1]区段的相同真前后缀的长度。说到在透彻一些就是 j = next[j]，这句语句减少了无用的比较。

有没有想过，为什么next的第一个值为-1呢？

　　第一，

　　　　程序刚运行时，j是被初始为-1，直接进行 Pattern[i] == Pattern[j] 判断无疑会边界溢出；

　　第二，

　　　　else语句中j = next[j]，j 是不断后退的，若 j 在后退中被赋值为 -1（也就是 j = next[0]），在 Pattern[i] == Pattern[j] 判断也会边界溢出。

　　综上，其意义就是为了特殊边界判断，而且 j 一开始被赋值为-1，比较方便给第二项赋值。

四、KMP样例实现

　　最好自己实现一遍！！！

 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>

 int KMP(char* MainString, char* Pattern);
 void GetNext(char* Pattern, int next[]);

 int main()
 {
     printf("%d\n",KMP("ljhgfdsa asdfghjkl\0", "dfghj\0"));
 }

 int KMP(char* MainString, char* Pattern)
 {
     int next[] = {};
     GetNext(Pattern, next);

     int i = ;
     int j = ;
     int s_len = strlen(MainString);
     int PatternLen = strlen(Pattern);

     while (i < s_len && j < PatternLen)
     {
         if (j == - || MainString[i] == Pattern[j])
         {
             i++;
             j++;
         }
         else
         {
             j = next[j];
         }
     }

     if (j == PatternLen)
     {
         return i - j;
     }

     return -;
 }

 void GetNext(char* Pattern, int next[])
 {
     int PatternLen = strlen(Pattern);
     int i = ;
     int j = -;
     next[] = -;

     while (i < PatternLen - )
     {
         if (j == - || Pattern[i] == Pattern[j])
         {
             i++;
             j++;
             next[i] = j;
         }
         else
         {
            j = next[j];
         }
     }
 }

KMP

五、KMP优化

　　还记得上面的那个问题吗？KMP不够完美的问题，其实只需要判断一下他们是不是相等的字符，然后进行处理即可。

　　处理方式：获取前一个字符的最长字串。

自己先试试

void GetNextval(char *Pattern, int nextval[])
{
    int p_len = strlen(Pattern);
    int i = ;
    int j = -;
    nextval[] = -;

    while (i < p_len - )
    {
        if (j == - || Pattern[i] == Pattern[j])
        {
            i++;
            j++;

            //优化
            if (Pattern[i] != Pattern[j])
            {
                nextval[i] = j;
            }
            else
            {
                nextval[i] = nextval[j];    \\一样的时候最长字串来源于前一个
            }
        }
        else
        {
            j = nextval[j];
        }
    }
}

getnext优化

KMP算法（未优化版）： next数组表示最长的相同真前后缀的长度，我们不仅可以利用next来解决模式串的匹配问题，也可以用来解决类似字符串重复问题等等，这类问题大家可以在各大OJ找到。

KMP算法（优化版）： 根据代码很容易知道（名称也改为了nextval），优化后的next仅仅表示相同真前后缀的长度，但不一定是最长（称其为“最优相同真前后缀”更为恰当）。此时我们利用优化后的next可以在模式串匹配问题中以更快的速度得到我们的答案（相较于未优化版），但是上述所说的字符串重复问题，优化版本则束手无策。