Tukey法
Tukey法
在介绍Tukey方法前,首先了解学生化极差分布。
在概率论和统计学中,学生化极差分布是极差的抽样分布。该分布是一种连续型概率分布,用于在样本量较小且总体标准差未知的情况下估计正态分布总体的极差。
假设要比较的组数为k,那么在零假设成立的条件下,下面的随机变量服从学生化极差分布。
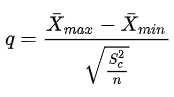



Tukey法的更多相关文章
- Bonferroni校正法
Bonferroni校正:如果在同一数据集上同时检验n个独立的假设,那么用于每一假设的统计显著水平,应为仅检验一个假设时的显著水平的1/n http://baike.baidu.com/view/12 ...
- SAS学习笔记26 方差分析
对于多于两组(k>2)样本均数的比较,t检验不再适用,方差分析(analysis of variance, ANOVA)则是解决上述问题的重要分析方法.方差分析由R.A.Fisher(1923) ...
- 《构建之法》阅读有疑 与 个人Week1作业
<构建之法>阅读有疑 在用将近五节课的时间将邹欣老师的书<构建之法——现代软件工程>第二版大致看完.虽然全书是以轻松的口吻与”移山公司”员工的一些趣味谈话来传输一些理念和思想的 ...
- SAGE|DNA微阵列|RNA-seq|lncRNA|scripture|tophat|cufflinks|NONCODE|MA|LOWESS|qualitile归一化|permutation test|SAM|FDR|The Bonferroni|Tukey's|BH|FWER|Holm's step-down|q-value|
生物信息学-基因表达分析 为了丰富中心法则,研究人员使用不断更新的技术研究lncRNA的方方面面,其中技术主要是生物学上的微阵列芯片技术和表达数据分析方法,方方面面是指lncRNA的位置特征. Bac ...
- SE_Work1_阅读构建之法&项目管理实践
项目 内容 课程:北航-2020-春-软件工程 博客园班级博客 要求:阅读<构建之法>并回答问题 个人博客作业 我在这个课程的目标是 提升团队管理及合作能力,开发一项满意的工程项目 这个作 ...
- [C#] 软硬结合第二篇——酷我音乐盒的逆天玩法
1.灵感来源: LZ是纯宅男,一天从早上8:00起一直要呆在电脑旁到晚上12:00左右吧~平时也没人来闲聊几句,刷空间暑假也没啥动态,听音乐吧...~有些确实不好听,于是就不得不打断手头的工作去点击下 ...
- 0-1背包问题蛮力法求解(c++版本)
// 0.1背包求解.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h" #include <iostream> #define ...
- 算法笔记_013:汉诺塔问题(Java递归法和非递归法)
目录 1 问题描述 2 解决方案 2.1 递归法 2.2 非递归法 1 问题描述 Simulate the movement of the Towers of Hanoi Puzzle; Bonus ...
- Matlab slice方法和包络法绘制三维立体图
前言:在地球物理勘探,流体空间分布等多种场景中,定位空间点P(x,y,x)的物理属性值Q,并绘制三维空间分布图,对我们洞察空间场景有十分重要的意义. 1. 三维立体图的基本要件: 全空间网格化 网格节 ...
随机推荐
- python数组定义
转自:https://blog.csdn.net/minsenwu/article/details/7872679 Python中没有数组的数据结构,但列表很像数组,如: a=[0,1,2],这时a[ ...
- JavaEE--JNDI(下,实现)
参考:https://blog.csdn.net/ouyida3/article/details/46699023 https://www.landui.com/help/show-6158.htm ...
- JZOJ-2019-11-5 B组
T1 给出一二维01矩阵\(f_{i,j}\), 定义点\((x_a, y_a), (x_b, y_b)\)的「距离」为\(max\{|x_a-x_b|, |y_a-y_b|\}\) 求出一矩阵\(w ...
- MySQL 插入 中文数据乱码解决
问题描述: 1.在命令行中进行插入,没有问题.但是显示存在部分乱码 2.在JDBC中插入成功.中文是直接以“??”形式显示. 通过Navicat客户端查看 与在网页中看到的一一致,说明读取没有问题,问 ...
- oracle 向表中插入BLOB类型数据
提示: 待插入图片必须保存到oracle主机路径上. 步骤: 1.SYSDBA权限用户创建图片所在目录 CREATE OR REPLACE DIRECTORY TEST_DIR AS 'C:\Pict ...
- import datetime
import datetimenow = datetime.datetime.now()print('当前时间:',now) 当前时间: 2019-11-21 11:11:58.093122
- tomcat8.5的安装、卸载、配置和部署
安装和卸载 下载 http://tomcat.apache.org/ 环境变量 1.点击此电脑 右键—>属性. 2.创建变量名为CATALINA_HOME,的值为所解压安装tomcat的本地目录 ...
- LeetCode No.166,167,168
No.166 FractionToDecimal 分数到小数 题目 给定两个整数,分别表示分数的分子 numerator 和分母 denominator,以字符串形式返回小数. 如果小数部分为循环小数 ...
- VCPU的解释
vCPU,顾名思义,是虚拟CPU. 创建虚拟机时,需要配置vCPU资源. 因此vCPU是虚拟机的部件. 因此脱离VM,谈论vCPU是没有意义的. 虚拟化管理系统如何调度vCPU,取决于系统内的虚拟机数 ...
- py02_04:三元运算法
a if a > b else c # a>b 成立,则为真,如果a>b为假,则返回c
