[Alg] 文本匹配-单模匹配-KMP

1. 暴力求解

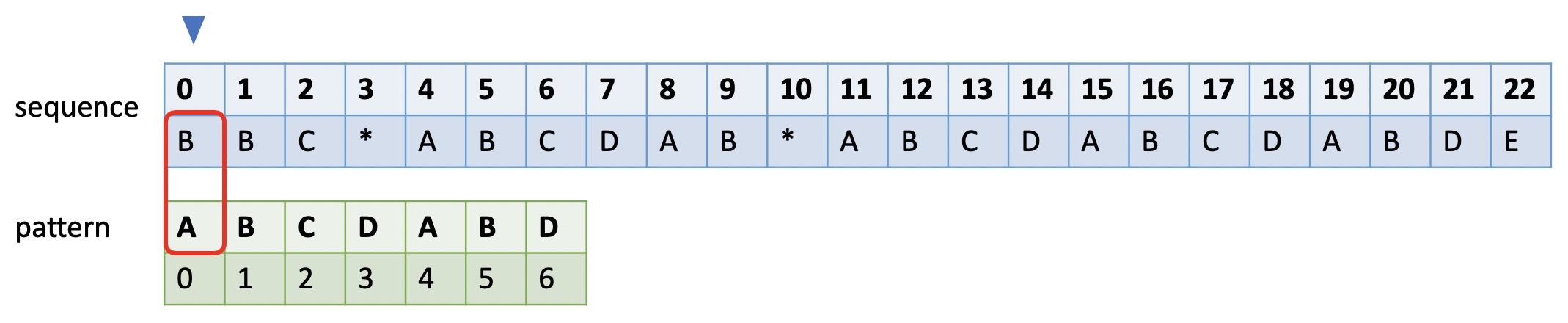
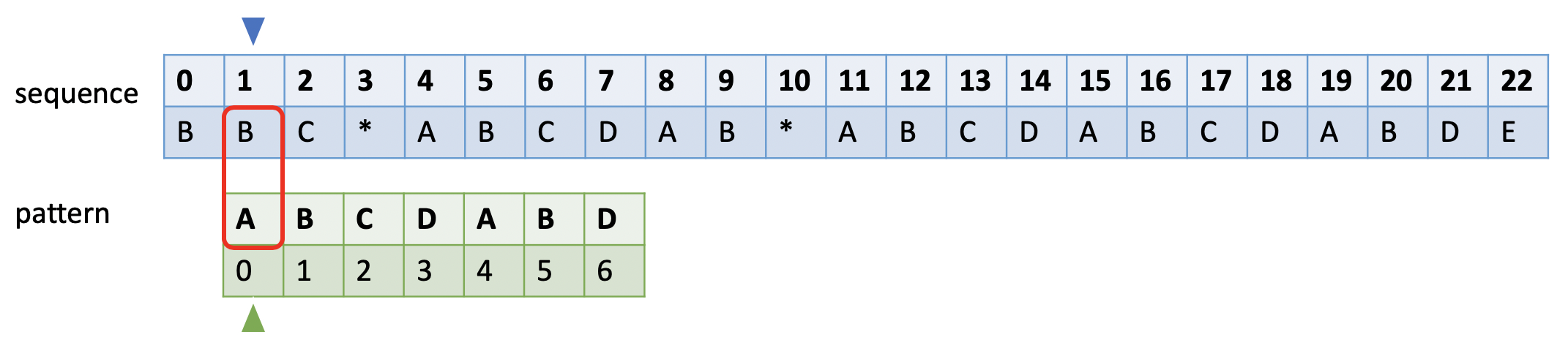
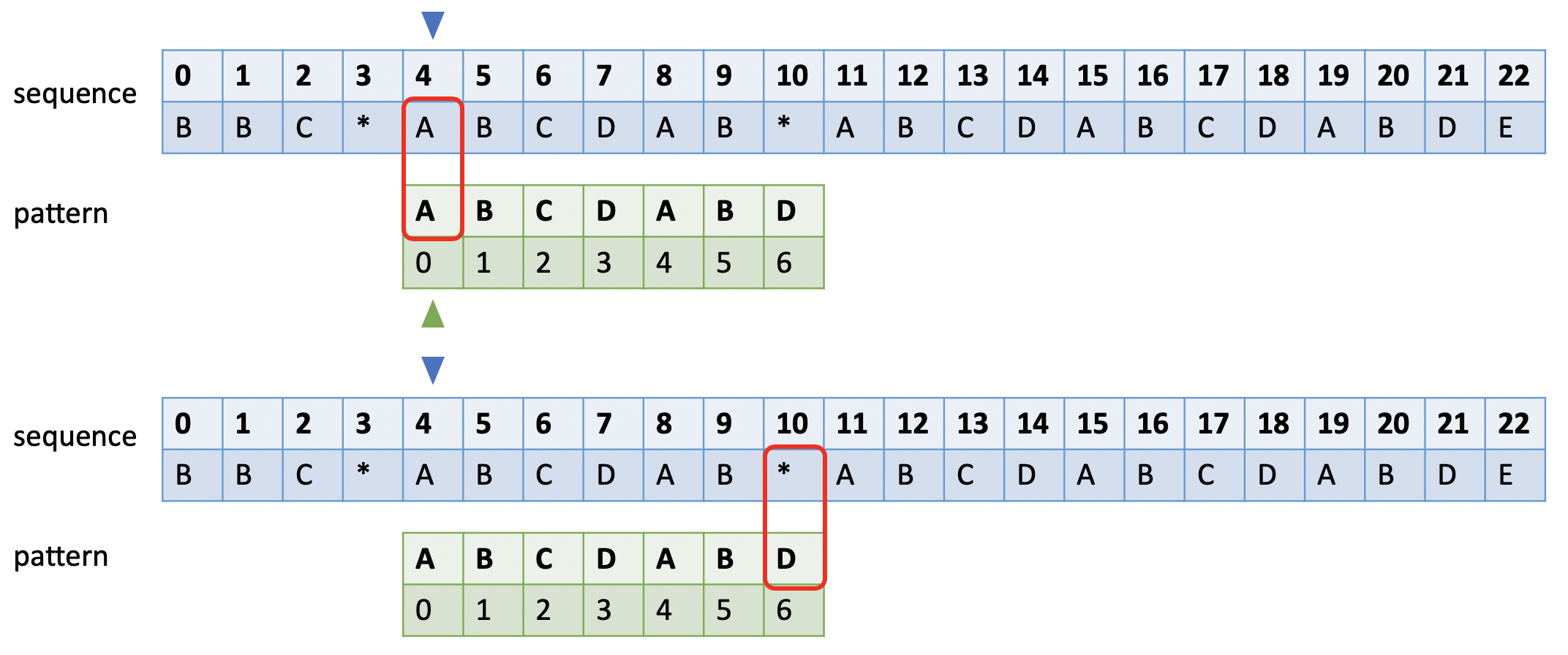
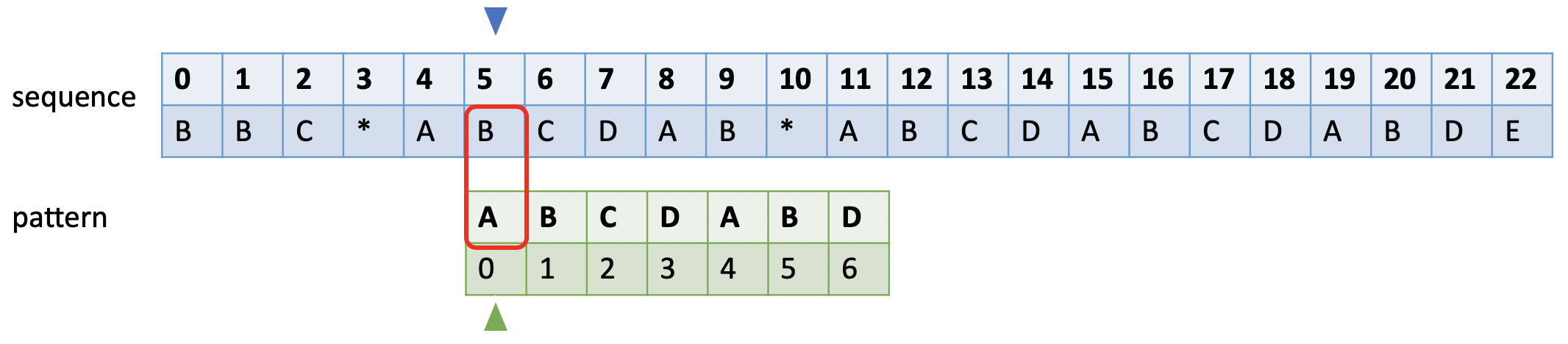
如下图所示。蓝色的小三角表示和sequence比较时的开始字符，绿色小三角表示失败后模式串比对的开始字符，红色框表示当前比较的字符对。

当和模式串发生不匹配时，蓝色小三角后移一位，绿色小三角移到模式串的第0位。

如果sequence长度为m, pattern长度为n，暴力求解的时间复杂度：O(m * n)

2. KMP算法

暴力求解中"当和模式串发生不匹配时，蓝色小三角后移一位，绿色小三角移到模式串的第0位。"能不能多移几位呢？

在发生不匹配之前，我们已经比较一些字符，这些字符内部有什么可以被我们利用的特征呢？

2.1 举个例子

2.1.1 例子1

上图中，pattern_1表示移动前的pattern，pattern_2表示发生了不匹配后用KMP算法移动后的pattern。

我们希望的效果是，既然sequence串到index_s = 10之前都已经和模式串p比较过了，尽量不要再回退回去(退到index_s = 4的下一位即index_s = 5)重新比较了，从index_s =10继续比较就好了。那对于模式串应该从index_p为多少开始比较，可以保证index_p之前的子串均与sequence中index_s 之前的子串匹配呢？

如上图所示，已经匹配过的子串是sub = "ABCDAB"。看pattern串，其前缀p_part1 = 后缀p_part2. 而pattern串的后缀 p_part2 = 当前匹配的sequence串的s_part.

$$ p\_part1 = p\_part2 = s\_part $$

那么把pattern串移动到和当前匹配的sequence串后缀对应的位置上，(如pattern_2所示)就一定可以保证 s_part = part_1，那么从 sequence的index_s = 10 和 pattern的 index_p = 2继续比较就可以了。

因此，无论在sequence的哪个位置发生了不匹配，都不用移动当前sequence的待比较index_s，也就是寻找下一个待比较的sequence字符和pattern字符时，和sequence是解耦的。

唯一有影响的就是已经匹配过的pattern子串。对于pattern串，在index_p位置与sequence发生了不匹配，而已经匹配过的pattern的子串有 p_part1 = p_part2，因此下一次只需要用

p_part1部分的下一个元素和index_s处元素比较就可以了。它们之前的子串一定是相同匹配的（如图sequence和pattern_2中，s_part = p_part2）。

OK，那么寻找已经匹配的子串的相同前缀后缀元素，之后让pattern移动后的前缀 和 移动前的后缀对应起来，它们一定匹配，那么继续向后比较就可以了。

2.1.2 例子2

但是有一个问题，如果已经匹配过的子串前缀后缀相同元素有多种可能的情况，应该怎么移动？

比如 sub = "AAABAAA"。

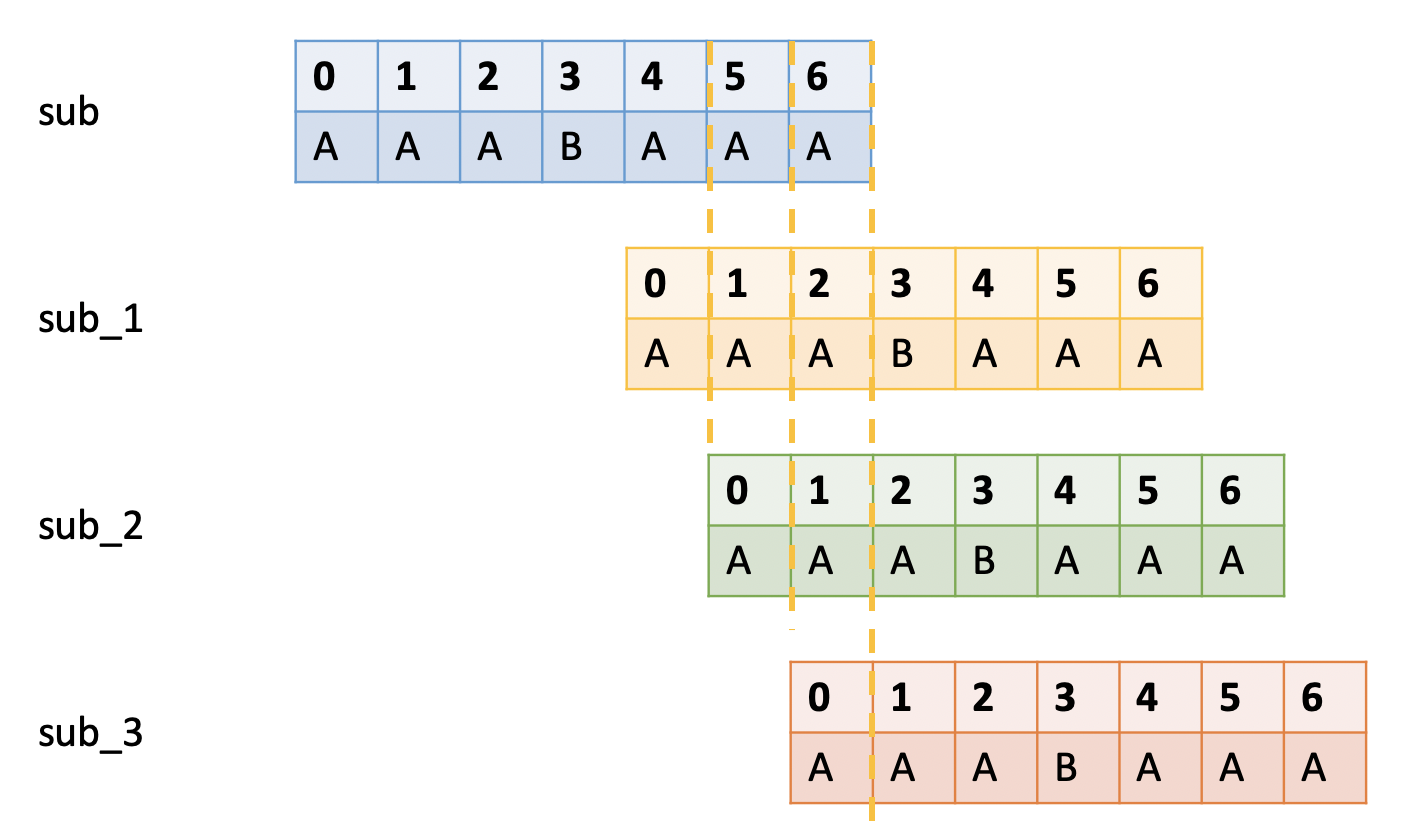
有3中可能的移动方式，匹配3位(sub_1)，2位(sub_2)还是1位后缀(sub_3)？

不难看出，应该匹配最长前缀后缀元素的sub_1。如果选择了sub_2或是sub_3，则可能出现漏查。

2.2 基本概念

以上例子可以抽象出来两个概念，一个是 前缀后缀的最长公共元素；一个是next数组。

前缀后缀的最长公共元素：已匹配过的子串的最长相同的 前缀和后缀的 元素。例子1，对于sub = "ABCDAB", 前缀后缀的最长公共元素就是"AB"。例子2，对于sub = "AAABAAA"， 前缀后缀的最长公共元素就是"AAA"。也就对应图中符号p_part1, p_part2.

next数组：由上面的例子可知，匹配失败后寻找下一个待匹配的元素对，可以和sequence解耦，只看pattern。在pattern的不同位置发生了不匹配，都可以通过pattern串本身的特征找到下一个待匹配的元素位置。那么可以用一个数组记录下，在pattern串各位发生了不匹配时候，下一个要比较的pattern的元素的位置。就是next数组。next[j] = k 代表p[j] 之前的模式串子串中，有长度为 k 的相同前缀和后缀，即前缀 [0 ~ (k - 1)] 与 后缀 [(j - k) ~ (j - 1)] 对应匹配。

2.3 next数组的建立

KMP算法的关键就是next数组的建立。

next数组初始化next[0] = -1，对于之后的值，可以通过递推的方法来求。已知next[0]...next[j]，求next[j + 1] = ?

这里记 next[j] = k，next[k] = k'。

next[j] = k 表示在pattern的 j 处发生了不匹配时，最长的相同前缀后缀元素长度为 k, 即前缀 [0 ~ (k - 1)] 长度为k的子串与 后缀 [(j - k) ~ (j - 1)] 长度为k的子串是匹配的。

求next[j + 1]，就要看在 j + 1 位置之前，最长的相同前缀后缀元素是多长，那么p[k] 和 p[j]是否相同就很关键。如果二者相同，则相比于next[j]，最长的相同前缀后缀元素长度就可以加一。如果不相同，那么就需要从 前缀子串 [0 ~ (k - 1)] 中再截一段更短前缀，使之与后缀匹配。

(1) 若 p[k] == p[j]，则next[j + 1] = next[j] + 1 = k + 1

由上图易知，前缀的最后一位从黄色正立小三角位置移动到红色正立小三角位置；后缀的最后一位从黄色倒立小三角位置移动到红色倒立小三角位置。

(2) 若 p[k] != p[j]，则递推 k' = next[k] 

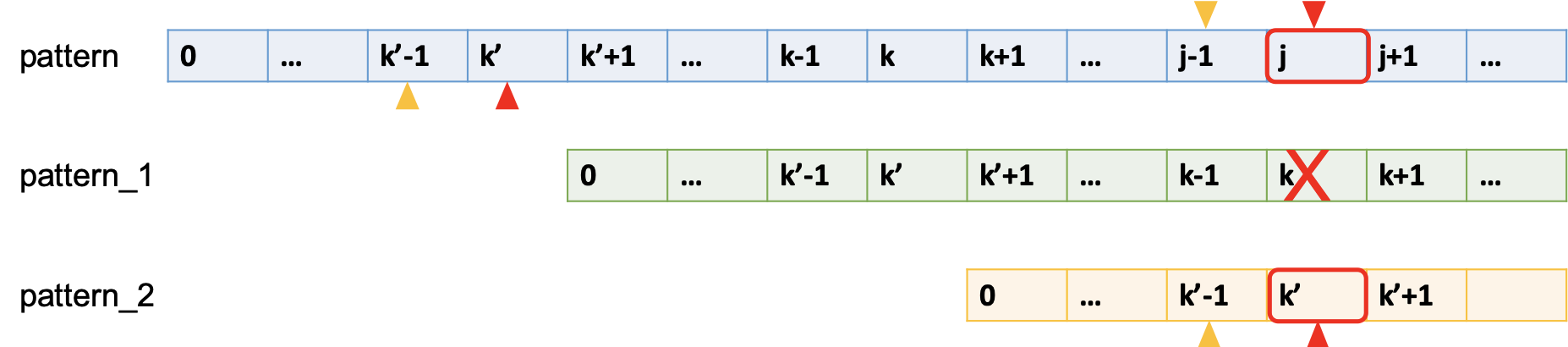
那么最长相同前缀后缀元素就在k处断掉了，所以，最长相同前缀不是pattern_1.

递推 k' = next[k] ，判断 p[k'] ?= p[j].

(如上图 pattern_2 黄色正立小三角及之前子串表示前缀part_1， pattern 倒立黄色小三角及之前长度为 k' + 1 子串表示后缀part_2，它们是对应匹配的。)

a) 若p[k'] == p[j]，则 next[j + 1] = k' + 1。

b) 若p[k'] != p[j]，返回(2), 继续递推 k'' = next[k']。

2.4 next数组的优化

以该图为例，还是求next[j + 1]。现在假设 p[k] == p[j]，是否就要设定 next[j + 1] = k + 1?

分析：next[j + 1]表示如果p[j + 1] != s[index_s]，那么就继续比较 p[next[j + 1]] 和 s[index_s]。但是，如果 p[next[j + 1]] = p[k + 1] = p[j + 1]，那必然和 s[index_s]不匹配。所以在最初建立next数组时候就要加入这个考虑，继续递推k = next[j]直到 p[j + 1] != p[k + 1]。

3. 代码实现

def getNEXT(p):
    len_p = len(p)
    NEXT = [-1] * len_p
    NEXT[0] = -1
    # k: indicator of prefix
    # j: indicator of suffix
    k = -1
    j = 0

    while j < len_p - 1:
        if k == -1 or p[k] == p[j]:
            k += 1
            j += 1
            while p[j] == p[k]:
                k = NEXT[k]
            if p[j] != p[k]:
                NEXT[j] = k
        else:
            k = NEXT[k]

    return NEXT

def KMPSearch(s, p, NEXT):
    i = 0
    j = 0
    len_s = len(s)
    len_p = len(p)
    while i < len_s and j < len_p:
        if j == -1 or s[i] == p[j]:
            i += 1
            j += 1
        else:
            j = NEXT[j]

    if j == len_p:
        return i - j
    else:
        return -1

s = "BBC ABCDAB ABCDABDABDE"
p = "ABCDABD"
NEXT = getNEXT(p)
ret = KMPSearch(s, p, NEXT)
print(ret)

参考链接：

1. 从头到尾彻底理解KMP：https://www.cnblogs.com/zhangtianq/p/5839909.html