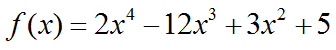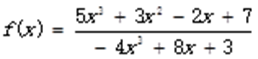MATLAB练习

第六章数据分析与多项式计算

1、max和min

1、分别求矩阵A中各列和各行元素中的最大值。max和min的用法一样
 % 【例6.1】分别求矩阵中各列和各行元素中的最大值。

A=[54,86,453,45;90,32,64,54;-23,12,71,18];
y1=max(A);   %求矩阵A中各列元素的最大值
y2=max(A,[],2)   %求矩阵A中各行元素的最大值

y2 =

   453
    90
    71

>> y1

y1 =

    90    86   453    54

    
2、求矩阵X、Y所有同一位置上的较大元素构成的新矩阵p。

>> X=[443,45,43;67,34,-43];
>> Y=[65,73,34;61,84,326];
>> p=max(X,Y);%两矩阵元素的同一位置比较，返回最大值
p =
   443    45    45
    67    45    45

3、将矩阵A的元素与常数x比较，返回较大的元素，构成同A阶数相同的矩阵，元素取

>> x=45;
>> p=max(A,x);
p =
   443    45    45
    67    45    45

2、求和sum(A)和sum(X,dim)、求积prod用发同sum

求矩阵A的每行元素之和和全部元素之和。
>> A=[9,10,11,12;100,200,300,400;50,60,50,60];
>> S=sum(A,2)   %求A每行元素的和
S =
          42
        1000
         220
>> p=sum(A)   %求A的全部元素之和
P =
   1262

3、求平均值和中值

求平均数格式：
M=mean(X);    X:向量或者矩阵 
M=mean(A,dim);  dim=1或2(行)
求中值格式：
M=median(X);    X:向量或者矩阵 
M=median(A,dim);  dim=1或2(列)
 
例如，求向量x = [-8，2，4，7，9]与y = [-8，2，4，7，9，15]的平均值和中值。

>> x=[-8,2,4,7,9];            % 奇数个元素
>> mx=[mean(x),median(x)]
mx =
    2.8000    4.0000
>> y=[-8,2,4,7,9,15];           % 偶数个元素
>> my=[mean(y), median(y)]
my =
    4.8333    5.5000

4、求累加和与累乘积

累加格式：
B = cumsum(X)；      X：向量或矩阵
B = cumsum(X,dim)：  dim：1或2(列)
累乘积用法同累加和
B = cumprod(X)；      X：向量或矩阵
B = cumprod(X,dim)：  dim：1或2(列)
列【例6.4】求S=1+（1+2）+(1+2+3)+…+(1+2+…+10)的值。

>> y=cumsum(1:10)
y =
     1     3     6    10    15    21    28    36    45    55
>> s=sum(y)
s =
   220

5、统计描述函数

1、标准差

调用格式
s = std(X , w, dim)   X矩阵或者行向量，w：用于指定标准差的计算方法；w=0或1  dim=1或2(求行元素标准差)
某次射击选拔比赛中小明与小华的10次射击成绩（单位：环）如表6.1所示，试比较两人的成绩。
小明：7,4,9,8,10,7,8,7,8,7
小华：7,6,10,5,9,8,10,9,5,6

>> hitmark=[7,4,9,8,10,7,8,7,8,7;7,6,10,5,9,8,10,9,5,6];
>> mean(hitmark,2)；    %按行求平均值，返回一个列向量
ans =
    7.5000
    7.5000
>> std(hitmark,[],2)；按行求标准差，返回一个列向量
ans =
    1.5811
    1.9579

　注意：标准差越小，成绩波动越小

2、方差

var函数的调用格式为
V = var(X, w, dim)    x：向量或者矩阵   w用于指定权重方案(为0:或为1)   dim=1(求各列方差)或2

考察一台机器的产品质量，判定机器工作是否正常。根据该行业通用法则：如果一个样本中的14个数据项的方差大于0.005，则该机器必须关闭待修。假设搜集的数据如表6.2所示，问此时的机器是否必须关闭？

>> samples=[3.43,3.45,3.43,3.48,3.52,3.50,3.39,3.48,3.41,3.38,3.49,3.45,3.51,3.50];
>>var_samples=var(samples);
var_samples =
    0.0021

3、相关系数

[R,P]=corrcoef(X,Y)：     %R：相关系数矩阵，p:p值矩阵      X和我Y：
矩阵返回相关系数矩阵和p值矩阵。如果得到的p值矩阵的非对角线元素小于显著性水平（即90%置信区间，默认为 0.05），则R中的相应相关性被视为显著
[R,P]=corrcoef(X)     
【例6.7】随机抽取15名健康成人，测定血液的凝血酶浓度及凝血时间，数据如表6.3所示。分析凝血酶浓度与凝血时间之间的相关性。

>> density=[1.1,1.2,1.0,0.9,1.2,1.1,0.9,0.6,1.0,0.9,1.1,0.9,1.1,1,0.7];  %凝血酶浓度
>> cruortime=[14,13,15,15,13,14,16,17,14,16,15,16,14,15,17];   %凝血时间
>> [R,P]=corrcosf(density,cruortime)
R =
    1.0000   -0.9265
   -0.9265    1.0000

注意;R的绝对值接近1，说明相关程度高

4、协方差

C = cov(x)：
C = cov(x,y)
随机抽取15名健康成人，测定血液的凝血酶浓度及凝血时间，数据如表6.3所示。分析凝血酶浓度与凝血时间之间的相关性

>> density=[1.1,1.2,1.0,0.9,1.2,1.1,0.9,0.6,1.0,0.9,1.1,0.9,1.1,1,0.7];
>> cruortime=[14,13,15,15,13,14,16,17,14,16,15,16,14,15,17];
>> C=cov(density,cruortime)
C =
    0.0289   -0.2014
   -0.2014    1.6381

注意：如果两个变量的协方差是正值，说明两者是正相关的，即两个变量的变化趋势一致；如果协方差为负值，则说明两者是负相关的，即两个变量的变化趋势相反；如果协方差为0，说明两者之间没有关系

6排序

[Y,I]=sort(X, dim, mode)    Y是排序后的矩阵，而I记录Y中的元素在X中的位置，mode指明排序的方法，'ascend'（默认值）为升序，'descend'为降序
6.8】对二维矩阵A=[1,-8,5;4,12,6;13,7,-13];做各种排序

>> A=[1,-8,5;4,12,6;13,7,-13];
>> Y=sort(A,2,'descend')            %对A的每行按降序排序
Y =
     5     1    -8
    12     6     4
    13     7   -13
>> [X,I]=sort(A) %对A的每列按升序排序，矩阵I存储X各元素在A对应列中的行号
X =
     1    -8    -13
     4     7     5
    13    12     6
I =
     1     1     3
     2     3     1
     3     2     2

6.2多项式计算

6.2.1多项式的四则运算

1、多项式的加减运算

计算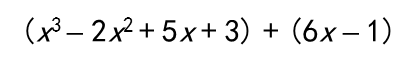

>> a=[1,-2,5,3];
>> b=[0,0,6,-1];
>> c=a+b
c =
     1    -2    11

2、多项式的乘除

w = conv(P1,P2)
[Q,r] = deconv(P1,P2)
P1、P2是两个多项式的系数向量
w是两个多项式相乘所得r
如果多项式

>> A=[1,8,0,0,-10];
>> B=[2,-1,3];
>> C=conv(A,B)
C =
     2    15    -5    24   -20    10   -30
>> [P,r]=deconv(A,B)
P =
        0.5000    4.2500    1.3750
r =
        0         0         0  -11.3750  -14.1250
以下命令验证deconv和conv是互逆的。
>> conv(B,P)+r
ans =
     1     8     0     0   -10

6.2.2多项式求导

k=polyder(P)：求多项式P的导数，即 
k=polyder(P,Q)：求P·Q的导数，即 
[q,d]=polyder(P,Q)：求P/Q的导数

>> P=[1];
>> Q=[1,0,5];
>> [p,q]=polyder(P,Q)
p =
    -2     0
q =
     1     0    10     0    25

6.2.3多项式的求值

1、代数多项式求值

y = polyval(p,x)   p是多项式系数向量。  x：标量，向量，矩阵

【例6.11】已知多项式x4 + 8x3 - 10，分别取x = 1.2和一个2 × 4矩阵为自变量计算该多项式的值。

>> A=[1,8,0,0,-10];       % 4次多项式系数
>> x=1.2;                 % 取自变量为一数值
>> y1=polyval(A,x)
y1 =
    5.8976
>> x=randi(9,2,4) %randi(imax,m,n)函数：生成一组值在[1, imax]区间均匀分布的随机整数，构建m × n矩阵
x =
     8     2     6     3
     9     9     1     5
>> y2=polyval(A,x) % 分别计算矩阵x中各元素为自变量的多项式之值
y2 =
        8182          70        3014         287
       12383       12383          -1        1615

2、矩阵多项式求值

polyval(P,A);   A.*A.*A-5*A.*A+8*ones(size(A))

polyvalm(P,A)  的含义为 A：方阵   A*A*A-5*A*A+8*eye(size(A))


以多项式x4 + 8x3 -10为例，取一个2 × 2矩阵为自变量分别用polyval和polyvalm计算该多项式的值。

>> A=[1,8,0,0,-10];             % 多项式系数
>> x=[-1,1.2; 2,-1.8];         % 给出一个矩阵x
>> y1=polyval(A,x)              % 计算代数多项式的值
y1 =
  -17.0000    5.8976
   70.0000  -46.1584
>> y2=polyvalm(A,x)             % 计算矩阵多项式的值
y2 =
  -60.5840   50.6496
   84.4160  -94.3504

6.2.4多项式的求根

x=roots(P)    P为多项式的系数向量

【例6.13】已知

（1）计算f(x) = 0的全部根。
（2）由方程f(x) = 0的根构造一个多项式g(x)，并与f(x)进行对比。

>> P=[2,-12,3,0,5];
>> X=roots(P)            %求方程f(x)=0的根
X =
5.7246 + 0.0000i
0.8997 + 0.0000i
  -0.3122 + 0.6229i
  -0.3122 - 0.6229i
>> G=poly(X)            %求多项式g(x)
G =
1.0000   -6.0000    1.5000   -0.0000    2.5000

6.2.5多项式的除法变换

[r,p,k] = residue(b,a)
[b,a] = residue(r,p,k)   
a、b 分别为分式的分母多项式、分子多项式的系数向量，r是分数多项式的商式的系数向量，p为分数多项式的极点，k为分数多项式的余式的系数向量
【例6.14】已知

（1）将f(x)进行分式分解。
（2）由分解的分式合成g(x)，并与f(x)进行对比。

>> b = [5 3 2 7];                %分子系数
>> a = [-4 0 8 3];               %分母系数
>> [r, p, k] = residue(b,a)       %r分数多项式的商式系数向量
r =
   -1.4167
   -0.6653
    1.3320
p =                                 %p为分数多项式的极点
    1.5737
   -1.1644
   -0.4093
k =
   -1.2500
>> [b,a] = residue(r,p,k)
b =
   -1.2500   -0.7500    0.5000   -1.7500
a =
    1.0000   -0.0000   -2.0000   -0.7500

6.3数据插值

6.3.1一维数据插值

vq = interp1(x,v,xq,method,extrapolation)
vq = interp1(x,v,xq,method,extrapolation)
x、v是两个等长的已知向量，分别存储采样点和采样值。若同一个采样点有多种采样值，则v可以为矩阵，v的每一列对应一种采样值。
输入参数xq存储插值点，输出参数vq是一个列的长度与xq相同、宽度与v相同的矩阵。
选项method用于指定插值方法,可取值如下。
    ‘linear’（默认值）：线性插值。
    ‘pchip’：分段3次埃尔米特插值
    ‘spline’：3次样条插值
    ‘ nearest’：最近邻点插值
    ‘next’：取最后一个采样点的值作为插值点的值
    'previous'：取前一个采样点的值作为插值点的值
    标量：设置域外点的返回值

【例6.15】表6.4所示为我国0~6个月婴儿的体重、身长参考标准，用3次样条插值分别求得婴儿出生后半个月到5个半月每隔1个月的身长、体重参考值。

>> tp=0:1:6;    %采样点
>> bb=[50.6,3.27;56.5,4.97;59.6,5.95;62.3,6.73;64.6,7.32;65.9,7.70;68.1,8.22]; %采样值
>> interbp=0.5:1:5.5;
>> interbv=interp1(tp,bb,interbp,'spline')   %用3次样条插值计算
interbv =
   54.0847    4.2505
   58.2153    5.5095
   60.9541    6.3565
   63.5682    7.0558
   65.2981    7.5201
   66.7269    7.9149

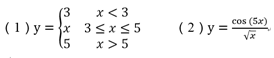
x1 = 1:7;
subplot(1,2,1)
y1=x1;
y1(x1<3)=3;
y1(x1>5)=5;
xq1 = 1:0.1:7;   %存储插值点
p1 = interp1(x1,y1,xq1,'pchip');   %分段3次埃尔米特插值
s1 = interp1(x1,y1,xq1,'spline');    %3次样条插值
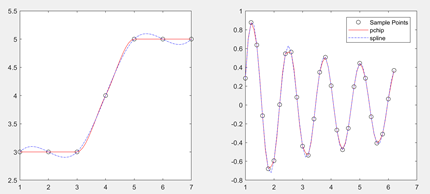
plot(x1,y1,'ko',xq1,p1,'r-',xq1,s1,'b-.') subplot(1,2,2) x2 = 1:0.2:2*pi;    %'ko':黑圆圈作为数据点标记
y2 = cos(5*x)./sqrt(x); xq2 = 1:0.1:2*pi;   
p2 = interp1(x2,y2,xq2,'pchip');
s2 = interp1(x2,y2,xq2,'spline'); plot(x2,y2,'ko',xq2,p2,'r-',xq2,s2,'b-.')； 
legend('Sample Points','pchip','spline')

6.3数据插值

6.3.1一维数据插值

vq = interp1(x,v,xq,method,extrapolation)
vq = interp1(x,v,xq,method,extrapolation)
x、v是两个等长的已知向量，分别存储采样点和采样值。若同一个采样点有多种采样值，则v可以为矩阵，v的每一列对应一种采样值。
输入参数xq存储插值点，输出参数vq是一个列的长度与xq相同、宽度与v相同的矩阵。
选项method用于指定插值方法,可取值如下。
    ‘linear’（默认值）：线性插值。
    ‘pchip’：分段3次埃尔米特插值
    ‘spline’：3次样条插值
    ‘ nearest’：最近邻点插值
    ‘next’：取最后一个采样点的值作为插值点的值
    'previous'：取前一个采样点的值作为插值点的值
    标量：设置域外点的返回值

【例6.15】表6.4所示为我国0~6个月婴儿的体重、身长参考标准，用3次样条插值分别求得婴儿出生后半个月到5个半月每隔1个月的身长、体重参考值。

>> tp=0:1:6;    %采样点
>> bb=[50.6,3.27;56.5,4.97;59.6,5.95;62.3,6.73;64.6,7.32;65.9,7.70;68.1,8.22]; %采样值
>> interbp=0.5:1:5.5;   %8存储插入点
>> interbv=interp1(tp,bb,interbp,'spline')   %用3次样条插值计算
interbv =
   54.0847    4.2505
   58.2153    5.5095
   60.9541    6.3565
   63.5682    7.0558
   65.2981    7.5201
   66.7269    7.9149

6.3.2网格数据插值

1、二维数据插值

其调用格式为

Zq=interp2(X, Y, V, Xq, Yq, method, extrapval)

X、Y分别存储采样点的平面坐标，V存储采样点采样值。

Xq、Yq存储插值点的平面坐标，Zq是根据相应的插值方法得到的插值点的值。

选项method的取值与一维插值函数相同，extrapval指定域外点的返回值。

【例6.17】表6.5所示为某企业从1968~2008年、工龄为10年、20年和30年的职工的月均工资数据。试用线性插值求出1973~1993年每隔5年、工龄为15年和25年的职工月平均工资。

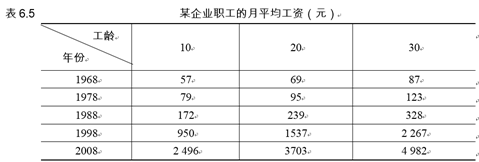
>> x=1968:10:2008;   %平面坐标的横坐标
>> h=[10:10:30].';   %平面坐标的纵坐标
>> W=[57,79,172,950,2496;
      69,95,239,1537,3703;
      87,123,328,2267,4982];
>> xi=1973:5:2003;   %存储采样点采样值
>> hi=[15;25];
>> WI=interp2(x,h,W,xi,hi)
WI =
   1.0e+03 *
    0.0750    0.0870    0.1462    0.2055    0.7245    1.2435    2.1715
    0.0935    0.1090    0.1963    0.2835    1.0928    1.9020    3.1223

2. 多维数据插值

MATLAB提供了3维、N维插值函数interp3、interpn，用法与interp2 一致。

Vq=interp3(X, Y, Z, V, Xq, Yq, Zq, method)

Vq=interpn(X1, X2,…,Xn, V, Xq1, Xq2,…,Xqn, method)

interp3函数的输入参数X、Y、Z以及interpn函数的输入参数 X1、X2、X3、...、Xn必须是网格格式。

6.3.3散乱数据插值

vq = griddata(x,y,v,xq,yq,method)

vq = griddata(x,y,z,v,xq,yq,zq,method)

x、y、z存储采样点的坐标，v是与采样点的采样值

xq、yq、zq存储插值点的坐标，vq是根据相应的插值方法得到的插值结果。

选项method指定插值方法，可取值如下。

‘linear’（默认值）:基于三角剖分的线性插值、
‘nearest’：基于三角剖分的最近邻点插值、
‘natural’：基于三角剖分的三次自然邻点插值、 
‘cubic’：基于三角剖分的三次插值，仅支持二维插值、
'v4'：双调和样条插值，仅支持二维插值

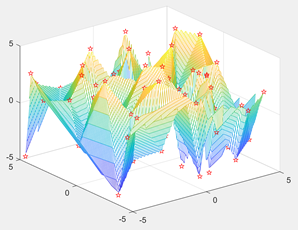
【例6.18】随机生成包含100个散点的数据集，绘制散点数据图和插值得到的网格数据图，观察插值结果。

xy=rand(100,3)*10-5;
x = xy(:,1);
y = xy(:,2);
z = xy(:,3);
[xq,yq] = meshgrid(-4.9:0.08:4.9, -4.9:0.08:4.9);
zq = griddata(x,y,z,xq,yq);
mesh(xq,yq,zq)
hold on
plot3(x,y,z,'rp')

　结果

6.4曲线拟合

polyfit函数的调用格式为
p = polyfit(x,y,n)
[p,S] = polyfit(x,y,n) 
[p,S,mu]=polyfit(X,Y,n)
x、y是两个等长的向量，存储采样点x和采样值y
产生一个n次多项式的系数向量p及其在采样点的误差向量S。p是一个长度为n + 1的向量，p的元素为多项式p1xn+p2xn−1+...+pnx+pn+1的系数。
mu是一个二元列向量，mu(1)是mean(x)， mu(2)是std(x)。
【例6.19】某研究所为了研究氮肥的施肥量对土豆产量的影响，做了十次实验，实验数据如表6.6所示。试分析氮肥的施肥量与土豆产量之间的关系

data=[0,15.18;34,21.36;67,25.72;101,32.29;135,34.03; ...
    202,39.45;259,43.15;336,43.46;404,40.83;471,30.75];
x=data(:,1);
y=data(:,2);
f=polyfit(x,y,2);
yi=polyval(f,x);
plot(x,y,'rp',x,yi)

6.5 非线性方程和非线性方程组的数值求解

6.5.1 非线性方程求解

求解一元连续函数F(x)的零点。
格式1：x=fzero(@fun,x0,options)     --->fun：函数名，x0：搜索起点。fzero只返回离x0最近的那个根。option为结构体变量。用于指定求解过程的优化参数。
格式2：[x,fval,exitflag,output]=fzero(@fun,x0,options)  --->fval返回目标函数在解x处的值，exitflag：返回求解过程终止原因，output ：返回寻根过程最优化的信息。
格式1为基本格式，格式2在函数寻根失败时返回寻根过程的错误和信息。
 
fzero的优化参数通常调用optimset函数设置，optimset函数的调用方法如下。options = optimset(优化参数1,值1, 优化参数2,值2,...)

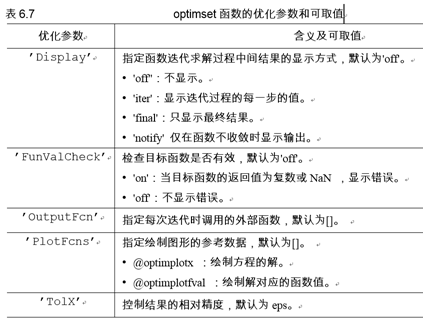
【例6.20】求 e -2x - x =0在x0 = 0附近的根

fzero的优化参数通常调用optimset函数设置，optimset函数的调用方法如下。

options = optimset(优化参数1,值1, 优化参数2,值2,...)

（1）建立函数文件funx.m。

function fx=funx(x)
 
fx=exp(-2*x)-x;

（2）调用fzero函数求根。

>> z=fzero(@funx,0.0)
 
z =
 
0.4263

如果要观测函数求根过程，可先设置优化参数，然后求解，命令如下。

>> options=optimset('Display','iter');%设定显示迭代求解的中间结果
 
>> z=fzero(@funx,0.0,options);

【例6.21】求下列非线性方程组在（0.5，0.5）附近的数值解。

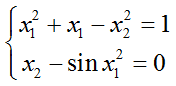
（1）建立函数文件myfun.m。

function q=myfun(p)
 
x1=p(1);
 
x2=p(2);
 
q(1)=x1^2+x1-x2^2-1;
 
q(2)=x2-sin(x1^2);

（2）在给定的初值（0.5，0.5）下，调用fsolve函数求方程的根。

x0=[0.5;0.5];
 
options = optimoptions('fsolve','Display','off'); %不显示中间结果
 
x= fsolve(@myfun,x0,options)
 
x =
 
0.7260
 
0.5029

matlab第六章数据分析与多项式计算的更多相关文章

MATLAB学习笔记（六）——MATLAB数据分析与多项式计算
(一)数据处理统计一.最大值和最小值 1.求向量的最大值和最小值 y=max(X); %返回向量X的最大值存入y,如果X中含有复数则按模最大的存入y [y,I]=max(X);%返回向量X的最大值存 ...
Java - 自定义异常(尚学堂第六章异常机制作业计算平均数)
编写一个计算N个学生分数平均分的程序.程序应该提示用户输入N的值,如何必须输入所有N个学生分数.如果用户输入的分数是一个负数,则应该抛出一个异常并捕获,提示“分数必须是正数或者0”.并提示用户再次输入 ...
Getting Started With Hazelcast 读书笔记(第五章,第六章)
第五章监听本章应该是Hazelcast的核心机制了,Hazelcast通过注册各种监听器获悉集群中其他应用对数据的修改,成员的加入,退出等. 分为3个层次. 1.EntryListener(对数据 ...
精通Web Analytics 2.0 （8）第六章：使用定性数据解答”为什么“的谜团
精通Web Analytics 2.0 : 用户中心科学与在线统计艺术第六章:使用定性数据解答"为什么"的谜团当我走进一家超市,我不希望员工会认出我或重新为我布置商店. 然而, ...
Java语言程序设计(基础篇) 第六章方法
第六章方法 6.2 定义方法 1.方法的定义由方法名称.参数.返回值类型以及方法体组成. 2.定义在方法头中的变量称为形式参数(formal parameter)或者简称为形参(parameter) ...
[Effective Java]第六章枚举和注解
声明:原创作品,转载时请注明文章来自SAP师太技术博客( 博/客/园www.cnblogs.com):www.cnblogs.com/jiangzhengjun,并以超链接形式标明文章原始出处,否则将 ...
Laxcus大数据管理系统2.0（8）- 第六章网络通信
第六章网络通信 Laxcus大数据管理系统网络建立在TCP/IP网络之上,从2.0版本开始,同时支持IPv4和IPv6两种网络地址.网络通信是Laxcus体系里最基础和重要的一环,为了能够利用有限的 ...
《Python核心编程》第六章序列 - 课后习题
课后习题 6–1.字符串.string 模块中是否有一种字符串方法或者函数可以帮我鉴定一下一个字符串是否是另一个大字符串的一部分? 答:成员关系操作符(in.not in) import string ...
C primer plus 读书笔记第六章和第七章
这两章的标题是C控制语句:循环以及C控制语句:分支和跳转.之所以一起讲,是因为这两章内容都是讲控制语句. 第六章的第一段示例代码 /* summing.c --对用户输入的整数求和 */ #inclu ...

随机推荐

Window+Protobuf使用说明
Window+Protobuf使用说明 C++WindowCmakeProtocbuf 介绍起因由于项目中要用到二进制存储数据,之前使用的方式是按照字节数依次将数据写入字节流中, 但是这样做起来做 ...
【shell】shell脚本入门
1. 前言 1.1 为什么学习shell编程 Shell脚本语言是实现Linux/UNIX系统管理及自动化运维所必备的重要工具,Linux/UNIX系统的底层及基础应用软件的核心大部分涉及Shell脚 ...
visual stdio 2012快捷键
为什么80%的码农都做不了架构师?>>> VS2012变化的快捷键:注释::VS2010是(Ctrl+E,C),VS2012是(Ctrl+K, Ctrl+C),实际操作,按住Ct ...
cobbler的网页操作
需求:安装一台服务器 1.指定两块网卡一块外网一块内网2.内网ip10.0.0.62外网为172.16.1.623.主机名为m02 开始吧! 1.添加镜像文件 2.创建ks文件编写ks文件附:ks ...
在 AutoLayout 和 Masonry 中使用动画
动画是 iOS 中非常重要的一部分,它给用户展现出应用灵气的一面. 在动画块中修改 Frame 在原来使用 frame 布局时,在 UIView 的 animate block 中对 view 的布局 ...
TCP 3-Way Handshake
TCP是面向连接的协议,其数据传输过程分为建立连接.数据传送.释放连接三个阶段. 0 建立连接建立连接的过程也就是常说的"三次握手": 客户端向服务器端发送一个SYN报文(SYN ...
2019年2月5日训练日记关于int字节数，long int 字节数的讨论
今天做到了个非常有意思的题目,是关于int最大最小值.用sizeof(int)查寻,返回四个字节,4个字节计算应该是4*8=32位,其中一位为符号位,且最高为不能为2所以应该减一,2^31-1=214 ...
Find Minimum in Rotated Sorted Array(旋转数组的最小数字)
题目描述: Suppose a sorted array is rotated at some pivot unknown to you beforehand. (i.e., might become ...
Python第三方库之Numpy库
概述 Numpy 最基本的库,是用于处理含有同种元素的多维数组运算的第三方库 —科学计算包,python数据分析及科学计算的基础库,几乎支撑所有其他库 —支持N维数组运算.处理大型矩阵.成熟的广播函 ...
2249: Altruistic Amphibians 01背包的应用 + lh的简单图论图转树求lca
第一个写了两个比较简单的数论题目,就是整除理论的两个题目,第一个题目比较蠢,第二个稍微要动一点脑筋 Codeforces Round #347 (Div. 2) – A. Complicated G ...

matlab第六章数据分析与多项式计算

MATLAB练习

第六章数据分析与多项式计算

1、max和min

2、求和sum(A)和sum(X,dim)、求积prod用发同sum

3、求平均值和中值

4、求累加和与累乘积

5、统计描述函数

1、标准差

2、方差

3、相关系数

4、协方差

6排序

6.2多项式计算

6.2.1多项式的四则运算

1、多项式的加减运算

2、多项式的乘除

6.2.2多项式求导

6.2.3多项式的求值

1、代数多项式求值

2、矩阵多项式求值

6.2.4多项式的求根

6.2.5多项式的除法变换

6.3数据插值

6.3.1一维数据插值

6.3数据插值

6.3.1一维数据插值

6.3.2网格数据插值

1、二维数据插值

2. 多维数据插值

6.3.3散乱数据插值

6.4曲线拟合

6.5 非线性方程和非线性方程组的数值求解

6.5.1 非线性方程求解

matlab第六章数据分析与多项式计算的更多相关文章

随机推荐

热门专题