#Week6 Neural Networks : Representation

一、Non-linear Hypotheses

线性回归和逻辑回归在特征很多时，计算量会很大。

一个简单的三层神经网络模型：

\[a_i^{(j)} = \text{"activation" of unit $i$ in layer $j$}$$$$\Theta^{(j)} = \text{matrix of weights controlling function mapping from layer $j$ to layer $j+1$}
\]

其中：$$a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{{(1)}x_3)$$$$a_2}{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{{(1)}x_3)$$$$a_3}{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3)$$$$h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0{(2)} + \Theta_{11}^{(2)}a_1{(2)} + \Theta_{12}^{(2)}a_2{(2)} + \Theta_{13}^{(2)}a_3{(2)})$$

二、vectorized implementation

将上面公式中函数\(g\)中的东西用\(z\)代替：

\[a_1^{(2)} = g(z_1^{(2)})$$$$a_2^{(2)} = g(z_2^{(2)})$$$$a_3^{(2)} = g(z_3^{(2)})
\]

令\(x=a^{(1)}\)：

\[z^{(j)} = \Theta^{(j-1)}a^{(j-1)}
\]

得到：

\[\begin{aligned}z^{(j)} = \begin{bmatrix}z_1^{(j)} \\ z_2^{(j)} \\ \cdots \\z_n^{(j)}\end{bmatrix}\end{aligned}
\]

这块的记号比较多，用例子梳理下：

实现一个逻辑与的神经网络：



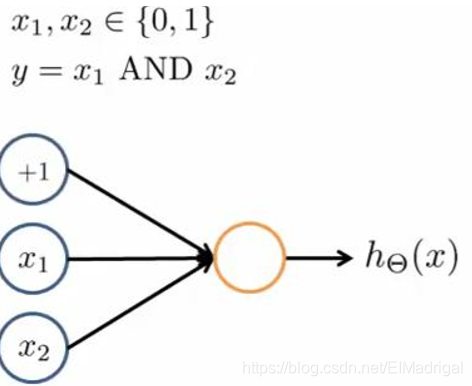
那么：





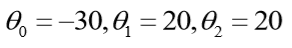
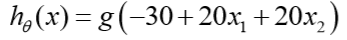
所以有：



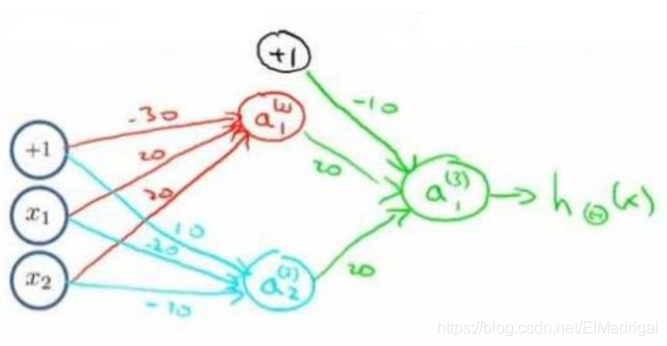
再来一个多层的，实现XNOR功能（两输入都为0或都为1，输出才为1）：



基本的神经元：

• 逻辑与
  
  
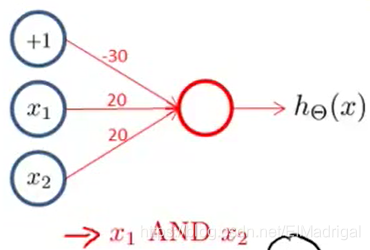
• 逻辑或
  
  
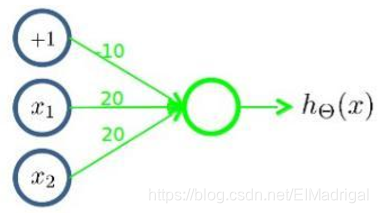
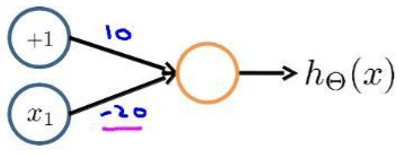
• 逻辑非
  
  
  
  先构造一个表示后半部分的神经元：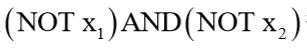
  
  这样的：
  
  
  
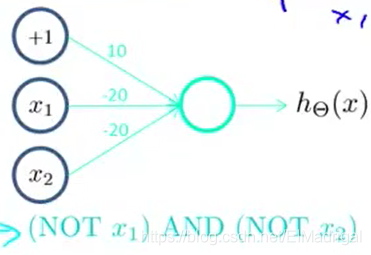
  接着将前半部分组合起来：
  
  

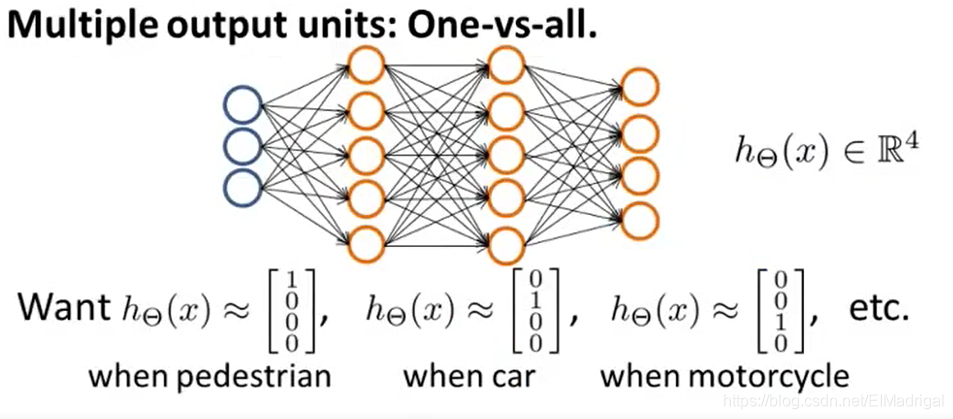
三、Multiclass Classification