DP+贪心水题合集_C++

本文含有原创题，涉及版权利益问题，严禁转载，违者追究法律责任

　　本次是最后一篇免费的考试题解，以后的考试题目以及题解将会以付费的方式阅读，题目质量可以拿本次作为参考

　　本来半个月前就已经搞得差不多了，然后给一位神犇orz看（神犇orz都是很忙的！），就一直听取意见修修改改呀拖到了半个月之后，不过这也是为了能够做到完美吧

T1-apple-1s

　　第一题是一道贪心的水题

　　

　　天数只有两天，不是今天吃就是明天吃，我们将 b[i]=min（x[i],y[i]）定为基础开心值，也就是说不论哪天吃都至少可以得到这个分数，于是只用考虑在哪天吃可以得到比基础更高的分数

　　那么我们将第一天的开心值减去第二天的开心值，得到一个差值，若为正数，则表示第一天比第二天优，若我们在第一天吃，那么除了得到基础的分数以外，还可以得到第一天多出的额外分数。如 x[1]=5，y[1]=3，不论在哪天吃至少可以得到 3 分，若在第一天吃还可以得到额外的 2 分

　　则将 b[i] 这个差值按降序排序，然后从前往后贪心即可

 #include<algorithm>
 #include<iostream>
 #include<cstdlib>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 
 struct data
 {
     long long n,a,b,x;
 }
     a[];
 long long n,m,i,ans;
 bool cmp(data x,data y)
 {
     return x.x>y.x;
 }
 int main()
 {
     freopen("apple.in","r",stdin);
     freopen("apple.out","w",stdout);
     cin>>n>>m;
     for (i=;i<=n;i++)
         {
             cin>>a[i].n>>a[i].a>>a[i].b;
             a[i].x=a[i].a-a[i].b;
         }
     sort(a+,a++n,cmp);
     for (i=;i<=n;i++)
         {
             if (m-a[i].n>=)
                 {
                     m-=a[i].n;
                     ans+=a[i].a*a[i].n;
                 }
             else
                 {
                     ans+=a[i].a*m+a[i].b*(a[i].n-m);
                     m=;
                 }
         }
     cout<<ans<<endl;
     return ;
 }

　　然后我来讲讲60分的做法，你强行不开 long long 就可以得到60分的高分！

T2-mos-1s

　　第二题DP，决策比较难想到，但是代码很容易写，原题是BZOJ2072和POI2004的，但BZOJ把题删了，POI根本上不去……坑爹呐，还是要贴上题目

　　先把时间升序排序，依次标号为1~n

　　我们考虑两种决策，第一种先让 1 号和 n 号过桥，然后 1 号返回，此时消耗 a[n]+a[1] 的时间，第二种是让 1 号和 2 号过桥，然后 1 号送回火把，n 号再跟 n-1 号过桥，最后 2 号送回火把，这样消耗 a[n]+2*a[2]+a[1] 的时间。显然第一种方案只能送走一个人，第二种方案可以送走两个人

　　这两种方案是最优的，但貌似证明比较难，这也导致了决策比较难想

　　设 f[i] 为送走到第 i 个人所用的时间，预处理出 f[n]=a[n]+a[1]，因为它不存在第二种两个人一起走的方案

　　状态转移方程   f[i]=min(a[i]+a[1]+f[i+1],a[i+1]+2*a[2]+a[1]+f[i+2])   i=n-1~3

　　目标状态就是 f[3]+a[2]

　　这里有一个点要特判，就是 n=1 或 2，此时答案就是 a[n]

 #include<algorithm>
 #include<iostream>
 #include<cstdlib>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 
 const int N=;
 int n,a[N],f[N];
 int main()
 {
     freopen("mos.in","r",stdin);
     freopen("mos.out","w",stdout);
     scanf("%d",&n);
     int i;
     for (i=;i<=n;i++) scanf("%d",&a[i]);
     sort(a+,a++n);
     if (n==||n==)
     {
         printf("%d\n",a[n]);
         return ;
     }
     f[n]=a[n]+a[];
     for (i=n-;i>;i--)    f[i]=min(a[i]+a[]+f[i+],a[i+]+*a[]+a[]+f[i+]);
     printf("%d\n",f[]+a[]);
     return ;
 }

T3-sta-2s

　　题目给的是两秒哈，然而极限数据最后被我0.998s跑过了

　　这题是BZOJ1131和POI2008的原题，结果跟上一题一样在网上已经失传了

　　话说大家都讲这是个树形DP模板题，然而我考场上没有做出来……

　　

　　设 f[x] 为以 x 为根的所有节点深度和，size[x] 为以 x 为根的树的节点个数+1（也就是后代的个数加上自己），fa[x] 为 x 的父亲节点

　　那么转移 f[x]=(f[fa[x]]-size[x])+(n-size[x])，把它按括号拆成两部分看，当根换成x后，对于它的父亲而言 x 节点的深度是少了 1 的，并且对于x的所有后代深度来说深度也都减少了1，即前半部分为原先总的深度 f[fa[x]] 减去因为换根少的深度 size[x]。后半部分也类似，除了x及其后代后的节点 n-size[x]，每一个深度都多了1，所以要加上

　　size 和 fa 数组用 DFS 预处理出来，我们用 f[1] 作为初始状态，它就是所有深度和，在预处理的时候统计统计，DP 用 BFS 转移

　　因为 n 很大，所以 DFS 的时候要手写栈

 #include<algorithm>
 #include<iostream>
 #include<cstdlib>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<stack>
 #include<queue>
 using namespace std;
 
 const int N=;
 stack<int> s;
 queue<int> q;
 int next[N*],first[N],v[N*],d[N],size[N],fa[N],j[N];
 long long f[N],k;
 bool g[N];
 inline void read(int &re)
 {
     char ch=getchar();
     re=;
     while (ch>=''&&ch<='')
     {
         re=re*+ch-'';
         ch=getchar();
     }
 }
 int main()
 {
     freopen("sta.in","r",stdin);
     freopen("sta.out","w",stdout);
     int i,x,n,m;
     read(n);
     for (i=;i<n;i++)
     {
         read(x);
         read(v[i]);
         next[i]=first[x];
         first[x]=i;
         v[i+n-]=x;
         next[i+n-]=first[v[i]];
         first[v[i]]=i+n-;
         size[i]=;
     }
     size[n]=;
     s.push();
     j[]=first[];
     fa[]=-;
     while (!s.empty())
     {
         x=s.top();
         for (;j[x];j[x]=next[j[x]])
             if (!fa[v[j[x]]])
             {
                 fa[v[j[x]]]=x;
                 k=d[v[j[x]]]=d[x]+;
                 f[]+=k;
                 j[v[j[x]]]=first[v[j[x]]];
                 s.push(v[j[x]]);
                 break;
             }
         if (!j[x])
         {
             s.pop();
             size[fa[x]]+=size[x];
         }
     }
     q.push();
     m=;
     while (!q.empty())
     {
         x=q.front();
         q.pop();
         for (i=first[x];i;i=next[i])
         {
             if (g[v[i]]) continue;
             g[v[i]]=;
             q.push(v[i]);
             k=n-size[v[i]]*;
             f[v[i]]=f[x]+k;
             if (f[v[i]]>f[m]||(f[v[i]]==f[m]&&v[i]<m)) m=v[i];
         }
     }
     printf("%d\n",m);
     return ;
 }

T4-tet-1s

　　BZOJ1106与POI2007的原题，BZOJ又把它删掉了T.T

　　考试的时候我用了一个奇奇怪怪的方法把它做出来了，虽然不是正解，但是可以A，还跑得挺快

　　

　　首先我们肯定是每次找最近的两个数字，然后通过交换把它们消去，如 1…2…1…2 这种情况先消去1还是先消去2的结果是一样的

　　设原栈为A，新建一个栈为B，每次将A栈顶元素取出丢进B里，如果B内已有相同元素，根据其距离B栈顶的距离更新答案，然后在栈中消去该数字。如果B内没有的话就压进栈，并且记录其位置，这样不断循环直到A为空为止

　　证明自己脑补一下（其实可以用“反正”法）

 #include<algorithm>
 #include<iostream>
 #include<cstdlib>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<stack>
 using namespace std;
 
 stack<int> a,b,c;
 int n,i,x,ans;
 bool f[];
 int main()
 {
     freopen("tet.in","r",stdin);freopen("tet.out","w",stdout);
     scanf("%d",&n);
     for (i=;i<=n*;i++) scanf("%d",&x),a.push(x);
     while (!a.empty())
         {
             x=a.top();
             a.pop();
             if (f[x])
                 {
                     while (b.top()!=x) c.push(b.top()),b.pop(),ans++;
                     b.pop();
                     while (!c.empty()) b.push(c.top()),c.pop();
                 }
             else f[x]=,b.push(x);
         }
     printf("%d\n",ans);
     return ;
 }

T5-bags-1s

　　RQNOJ 123，http://www.rqnoj.cn/problem/123

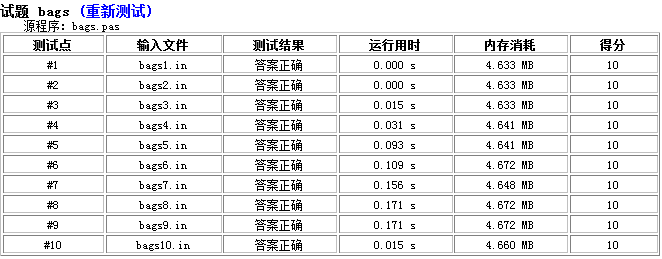
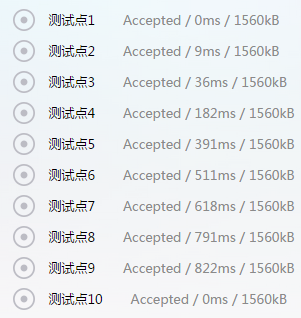
　　不得不说，RQNOJ的机子跑得好慢呀，5*10⁷ 的数据范围本地跑 0.2s，服务器上愣是把我卡掉了，最后只好写了一份 Pascal 交上去

　　本地跑

　　

　　OJ上跑

　　

　　咳咳，言归正传

　　普通的背包是求出最优的那一种方案，方程转移是 f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i])，相当于把 2 个变量经比较后丢到 1 个变量里，也就是 k=1 时的情况。而现在我们需要求最优的前 k 组方案，那么可以把数组再增加一维，变成把 2k 个变量经比较后丢进 k 个数里，也就是 2 个线性表丢进 1 个线性表里，由于线性表内数据是单调下降的，则可以按照归并排序的做法做

　　实现操作中还可以滚掉第一维，那么 j 就要递减枚举

 #include<algorithm>
 #include<iostream>
 #include<cstdlib>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 
 const int V=,K=,maxint=;
 int f[V][K],g[K];
 int main()
 {
     freopen("bags.in","r",stdin);
     freopen("bags.out","w",stdout);
     int i,j,n,m,s,ans=,q1,q2,k,w,v;
     scanf("%d%d%d",&m,&s,&n);
     for (i=;i<=s;i++)
         for (j=;j<=m;j++) f[i][j]=-maxint;
     f[][]=;
     for (i=;i<=n;i++)
     {
         scanf("%d%d",&w,&v);
         for (j=s;j>=w;j--)
         {
             if (f[j-w][]<) continue;
             q1=q2=;
             for (k=;k<=m;k++)
                 if (f[j-w][q1]+v>f[j][q2]) g[k]=f[j-w][q1++]+v;
                 else g[k]=f[j][q2++];
             for (k=;k<=m;k++) f[j][k]=g[k];
         }
     }
     for (i=;i<=m;i++) ans+=f[s][i];
     printf("%d\n",ans);
     return ;
 }

　　其实本来还准备了 3 道题的，不过那三道一道是国家集训队的作业题，一道是省队的考试题，最后一道是有版权的原创题（发了的话XXX会Heck我的QuQ）

　　那也就不能放进“水题”合集了吧

　　另外，所有题目均有数据出售，具体价格如下：

　　T1：RMB 1.0    T2：RMB 0.5    T3：RMB 0.5    T4：RMB 0.5    T5：自己到 OJ 上测去

　　如需购买请联系作者

　　联系方式：http://www.cnblogs.com/hadilo/p/5932395.html