【Foreign】划分序列 [线段树][DP]

划分序列

Time Limit: 20 Sec  Memory Limit: 256 MB

Description

　　

Input

　　

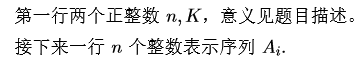
Output

　　仅一行一个整数表示答案。

Sample Input

　　9 4
　　1 1 1 3 2 2 1 3 1

Sample Output

　　5

HINT

　　

Main idea

　　将序列分为若干段，使得和最大的那一段最小，值可以为负。

Source

　　首先，显然都想到了二分答案。

　　我们先把都为正数或负数的情况写了：Ai>=0的时候求出最小的划分段数x，若x<=K则表示当前答案可行；Ai<=0的时候求出最大的划分段数x，若x>=K则表示当前答案可行。然后再打了暴力，接着我们对拍一下，惊讶地发现了一个规律：若最小划分段数为L，最大划分段数为R，当L<=K<=R时则可以更新。

　　然后我们用DP来求L和R，也就是：若一段的和满足<=mid，则可以分为一段。

　　然后我们发现，可以用线段树优化寻找1~i-1中的最小值或最大值，这样判断就可以满足效率了。

Code

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 #include<vector>
 using namespace std;
 typedef long long s64;
 
 const int INF = ;
 const int ONE = 5e4+;
 
 int n,block;
 int L,R;
 int x,sum[ONE],s[ONE];
 int li[ONE],li_num;
 int f_min[ONE],f_max[ONE];
 int res_min,res_max;
 int Zero;
 
 int get()
 {
         int res=,Q=;    char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }
 
 namespace Seg
 {
         struct power
         {
             int minn;
             int maxx;
         }Node[ONE];
 
         void Build(int i,int l,int r)
         {
             Node[i].minn = INF;
             Node[i].maxx = -INF;
             if(l==r) return;
             int mid=(l+r)>>;
             Build(i<<,l,mid);    Build(i<<|,mid+,r);
         }
 
         void Update(int i,int l,int r,int L,int x,int PD)
         {
             if(l==r)
             {
                 if(!PD) Node[i].minn = x;
                 else Node[i].maxx = x;
                 return;
             }
             int mid=(l+r)>>;
             if(L<=mid) Update(i<<,l,mid,L,x,PD);
             else Update(i<<|,mid+,r,L,x,PD);
             Node[i].minn = min(Node[i<<].minn, Node[i<<|].minn);
             Node[i].maxx = max(Node[i<<].maxx, Node[i<<|].maxx);
         }
 
         void Query(int i,int l,int r,int L,int R)
         {
             if(L<=l && r<=R)
             {
                 res_min=min(res_min, Node[i].minn);
                 res_max=max(res_max, Node[i].maxx);
                 return;
             }
             int mid=(l+r)>>;
             if(L<=mid) Query(i<<,l,mid,L,R);
             if(mid+<=R) Query(i<<|,mid+,r,L,R);
         }
 }
 
 int Check(int mid)
 {
         Seg::Build(,,li_num);
         Seg::Update(,,li_num, Zero,,);
         Seg::Update(,,li_num, Zero,,);
         for(int i=;i<=n;i++)
         {
             int pos = lower_bound(li+,li+li_num+,sum[i] - mid) - li;
             res_min = INF;    res_max = -INF;    Seg::Query(,,li_num, ,pos);
             f_min[i] = res_min + ;
             f_max[i] = res_max + ;
             Seg::Update(,,li_num, s[i],f_min[i],);
             Seg::Update(,,li_num, s[i],f_max[i],);
         }
         return (f_min[n]<=block && block<=f_max[n]);
 }
 
 int main()
 {
         n=get();    block=get();
         li[++li_num] = ;
         for(int i=;i<=n;i++)
         {
             x=get();
             li[++li_num] = sum[i] = sum[i-] + x;
             if(x < ) L+=x; else R+=x;
         }
 
         sort(li+,li+li_num+);
         li_num = unique(li+,li+li_num+) - li - ;
 
         for(int i=;i<=n;i++)
             s[i]=lower_bound(li+,li+li_num+, sum[i]) - li;
         Zero = lower_bound(li+,li+li_num+, ) - li;
 
         while(L < R - )
         {
             int mid=(L+R)>>;
             if(Check(mid)) R = mid;
             else L = mid;
         }
 
         if(Check(L)) printf("%d",L);
         else printf("%d",R);
 }