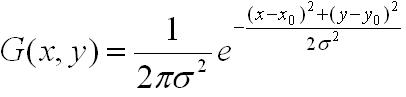图像金字塔、高斯金字塔、差分金字塔(DOG金字塔)、尺度空间、DoG (Difference of Gaussian)角点检测
【图像金字塔】
图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度像素采样的方式,生成N个不同分辨率的图像。把具有最高级别分辨率的图像放在底部,以金字塔形状排列,往上是一系列像素(尺寸)逐渐降低的图像,一直到金字塔的顶部只包含一个像素点的图像,这就构成了传统意义上的图像金字塔。
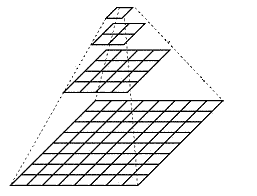
获得图像金字塔一般包括二个步骤:1. 利用低通滤波器平滑图像 ;2. 对平滑图像进行抽样(采样)。有两种采样方式——上采样(分辨率逐级升高)和下采样(分辨率逐级降低)
【高斯金字塔】
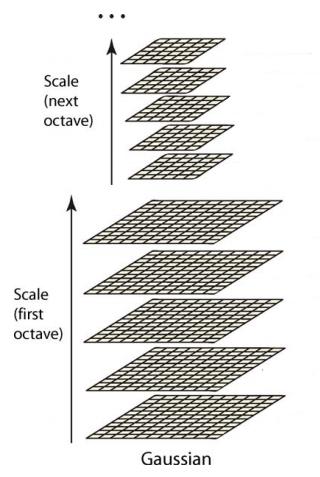
高斯金字塔式在Sift算子中提出来的概念,首先高斯金字塔并不是一个金字塔,而是有很多组(Octave)金字塔构成,并且每组金字塔都包含若干层(Interval)。
高斯金字塔构建过程:
1. 先将原图像扩大一倍之后作为高斯金字塔的第1组第1层,将第1组第1层图像经高斯卷积(其实就是高斯平滑或称高斯滤波)之后作为第1组金字塔的第2层,高斯卷积函数为:
对于参数σ,在Sift算子中取的是固定值1.6。
2. 将σ乘以一个比例系数k,等到一个新的平滑因子σ=k*σ,用它来平滑第1组第2层图像,结果图像作为第3层。
3. 如此这般重复,最后得到L层图像,在同一组中,每一层图像的尺寸都是一样的,只是平滑系数不一样。它们对应的平滑系数分别为:0,σ,kσ,k^2σ,k^3σ……k^(L-2)σ。
4. 将第1组倒数第三层图像作比例因子为2的降采样,得到的图像作为第2组的第1层,然后对第2组的第1层图像做平滑因子为σ的高斯平滑,得到第2组的第2层,就像步骤2中一样,如此得到第2组的L层图像,同组内它们的尺寸是一样的,对应的平滑系数分别为:0,σ,kσ,k^2σ,k^3σ……k^(L-2)σ。但是在尺寸方面第2组是第1组图像的一半。
这样反复执行,就可以得到一共O组,每组L层,共计O*L个图像,这些图像一起就构成了高斯金字塔,结构如下:
在同一组内,不同层图像的尺寸是一样的,后一层图像的高斯平滑因子σ是前一层图像平滑因子的k倍;在不同组内,后一组第一个图像是前一组倒数第三个图像的二分之一采样,图像大小是前一组的一半;
【DOG金字塔】
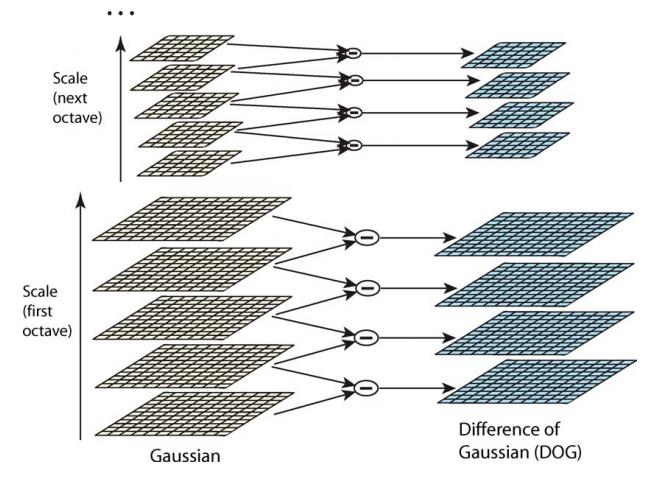
差分金字塔,DOG(Difference of Gaussian)金字塔是在高斯金字塔的基础上构建起来的,其实生成高斯金字塔的目的就是为了构建DOG金字塔。
DOG金字塔的第1组第1层是由高斯金字塔的第1组第2层减第1组第1层得到的。以此类推,逐组逐层生成每一个差分图像,所有差分图像构成差分金字塔。概括为DOG金字塔的第o组第l层图像是有高斯金字塔的第o组第l+1层减第o组第l层得到的。
DOG金字塔的构建可以用下图描述:
每一组在层数上,DOG金字塔比高斯金字塔少一层。后续Sift特征点的提取都是在DOG金字塔上进行的。
【尺度空间】
图像的尺度空间解决的问题是如何对图像在所有尺度下描述的问题。在高斯金字塔中一共生成O组L层不同尺度的图像,这两个量合起来(O,L)就构成了高斯金字塔的尺度空间,也就是说以高斯金字塔的组O作为二维坐标系的一个坐标,不同层L作为另一个坐标,则给定的一组坐标(O,L)就可以唯一确定高斯金字塔中的一幅图像。
尺度空间的形象表述:
上图中尺度空间中k前的系数n表示的是第一组图像尺寸是当前组图像尺寸的n倍。
【DoG 角点检测】
DoG (Difference of Gaussian)是灰度图像增强和角点检测的方法,其做法较简单,证明较复杂,具体讲解如下:Difference of Gaussian(DOG)是高斯函数的差分。我们已经知道可以通过将图像与高斯函数进行卷积得到一幅图像的低通滤波结果,即去噪过程,这里的Gaussian和高斯低通滤波器的高斯一样,是一个函数,即为正态分布函数。

那么difference of Gaussian 即高斯函数差分是两幅高斯图像的差,
一维表示: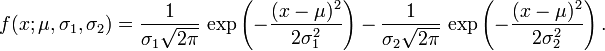
二维表示: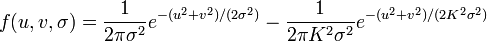
具体到图像处理来讲,就是将两幅图像在不同参数下的高斯滤波结果相减,得到DoG图。
1、处理一幅图像在不同参数下的DoG
A = Process(Im, 0.3, 0.4, x);
B = Process(Im, 0.6, 0.7, x);
C = Process(Im, 0.7, 0.8, x);
a = getExtrema(A, B, C, thresh);
2. 根据DOG求角点
DOG三维图中的最大值和最小值点是角点
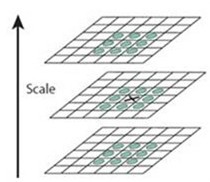
X标记当前像素点,绿色的圈标记邻接像素点,用这个方式,最多检测26个像素点。X被标记为特征点,如果它是所有邻接像素点的最大值或最小值点。因此在上一步计算出的A,B,C三个DOG图中求图B中是极值的点,并标记(max:1;min:-1)
【参考文献】
https://blog.csdn.net/dcrmg/article/details/52561656
https://blog.csdn.net/abcjennifer/article/details/7639488
图像金字塔、高斯金字塔、差分金字塔(DOG金字塔)、尺度空间、DoG (Difference of Gaussian)角点检测的更多相关文章
- DOG角点检测——opencv实现
1.原理 Difference of Gaussian(DOG)是高斯函数的差分.将两幅图像在不同参数下的高斯滤波结果相减,得到DoG图.步骤: 处理一幅图像在不同高斯参数下的DoG 用两个不同的5x ...
- OpenCV计算机视觉学习(13)——图像特征点检测(Harris角点检测,sift算法)
如果需要处理的原图及代码,请移步小编的GitHub地址 传送门:请点击我 如果点击有误:https://github.com/LeBron-Jian/ComputerVisionPractice 前言 ...
- Sift中尺度空间、高斯金字塔、差分金字塔(DOG金字塔)、图像金字塔
转自:https://blog.csdn.net/dcrmg/article/details/52561656 一. 图像金字塔 图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度像 ...
- 机器学习进阶-图像金字塔与轮廓检测-图像金字塔-(**高斯金字塔) 1.cv2.pyrDown(对图片做向下采样) 2.cv2.pyrUp(对图片做向上采样)
1.cv2.pyrDown(src) 对图片做向下采样操作,通常也可以做模糊化处理 参数说明:src表示输入的图片 2.cv2.pyrUp(src) 对图片做向上采样操作 参数说明:src表示输入的 ...
- Java 打印金字塔 or 打印带数字的金字塔 (Java 学习中的小记录)
Java 打印金字塔 or 打印带数字的金字塔 (Java 学习中的小记录) 作者:王可利(Star·星星) 效果图: 代码如下: class Star8 { public static void m ...
- java打印正金字塔,倒金字塔和“水影”金字塔
java打印正金字塔,倒金字塔和"水影"金字塔 --------原创文章,若要转载,请注明出处 小小少年 闲来无事,想起自己初学java的时候做的经典的无非就是打印出一些有意思 ...
- 用matlab给图像加高斯噪声和椒盐噪声(不调用imnoise函数)
图像画面中的噪声,大致可以分为两类:高斯噪声和椒盐噪声.在这里,我们先看下图像中两种噪声各自的特征. 椒盐噪声:噪声幅值基本相同,但出现位置随机. 高斯噪声:图像中每一点都存在噪声,但幅值是随机分布的 ...
- 机器学习进阶-图像特征harris-角点检测 1.cv2.cornerHarris(进行角点检测)
1.cv2.cornerHarris(gray, 2, 3, 0.04) # 找出图像中的角点 参数说明:gray表示输入的灰度图,2表示进行角点移动的卷积框,3表示后续进行梯度计算的sobel算子 ...
- Java中Animal b = new Dog();Dog c = new Dog();的区别
由于在编译阶段,只是检查参数的引用类型.然而在运行时,Java虚拟机(JVM)指定对象的类型并且运行该对象的方法.因此在下面的例子中,b.move()之所以能编译成功,是因为Animal类中存在mov ...
随机推荐
- 创建maven工程时报错,解决方案
解决思路:在本地库中装载maven-archetype-quickstart 1.从 http://mirrors.ibiblio.org/pub/mirrors/maven2/org/apache/ ...
- iPython notebook 安装使用
pip install jupyter jupyter notebook --allow-root
- jquery与原生js比较
以选择符为例,类似于这种 $(".class") 方式,在ie里面,肯定比$("#id") 低很多,而对于chrome和firefox,则因为提供了getEle ...
- tomcat在linux服务器上部署应用
连接服务器 服务器地址:xxx.xxx.xxx.xxx 用户名:xxxx 密码:xxxx 进入到服务器中的tomcat路径,关闭服务器,例如 路径:/opt/wzgcyth/apache-tomcat ...
- 720. Longest Word in Dictionary 能连续拼接出来的最长单词
[抄题]: Given a list of strings words representing an English Dictionary, find the longest word in wor ...
- mybatis 框架 的应用之二(批量添加、实现分页查询)
lf-driver=com.mysql.jdbc.Driver lf-url=jdbc:mysql://localhost:3306/test lf-user=LF lf-password=LF &l ...
- 基于 EntityFramework 的数据库主从读写分离架构 - 目录
基于 EntityFramework 的数据库主从读写分离架构 回到目录,完整代码请查看(https://github.com/cjw0511/NDF.Infrastructure)中的目 ...
- 使对象可以像数组一样foreach循环,要求属性必须是私有的(写个类实现Iterator接口)
<?php class Test implements Iterator { ,,,,); public function __construct() { } // 重置,将数组内部指针指向第一 ...
- 二度xml<一>
又一次学习Xml,之前差不多都忘了,为了下半年的面试,为了工作重头来过....... 其实我觉得直接上代码来的更实际点,理论的东西,我们随便找点书看看就行. 下面的代码是为了打印出一个xml文件 xm ...
- 企业管理系统——第三周需求&原型改进_张正浩,黄锐斌
企业管理系统——需求&原型改进,架构设计,测试计划 组员:张正浩,黄锐斌 一.需求&原型改进 1.给目标用户展现原型,与目标用户进一步沟通理解需求 我们的目标用户是公司管理员 场景:随 ...