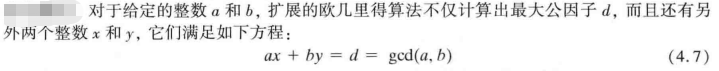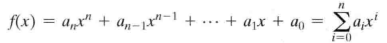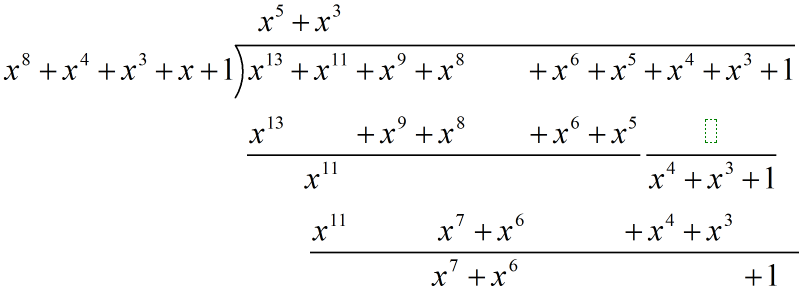AES128加密-S盒和逆S盒构造推导及代码实现
文档引用了《密码编码学与网络安全--原理和实践》里边的推导过程,如有不妥,请与我联系修改。
文档《FIPS 197》高级加密标准AES,里边有个S盒构造,涉及到了数论和有限域的一些概念,一脸懵逼,所以贱贱的研究了下,花了好久时间。
在网上找的S盒构造的详细步骤总是缺了点什么,要么步骤不详细,要么只贴了程序,难以搞清楚由几个基本概念一步一步推导出最终的S盒。最后,还是《密码编码学与网络安全--原理和实践》这本书讲得比较详细。教材果然还是经过精雕细琢过的,符合大部分人的认知过程。
这篇文章其一是记录下来这个学习步骤,其二是希望我的这篇能够更详细些。
先贴出来《FIPS 197》中对S盒构造的描述步骤:

就这两条。实际上是三个步骤,《密码编码学与网络安全--原理和实践》教材里会讲得更详细些。

一下都按照《密码编码学与网络安全--原理和实践》教材里边的三个步骤进行推导。
步骤1、3都比较浅显,即使没有数论和有限域概念,一样可以编程写出来。
步骤一:
根据行标号和列标号组合成16X16的二维数组,行标号作为高4bit,列标号作为低4bit;
生成代码如下:
1 for(i=0;i<0x10;i++)
2 {
3 for(j=0;j<0x10;j++)
4 {
5 s_box_ary[i][j] = ((i<<4)&0xF0) + (j&(0xF));
6 }
7 }
代码产生的数组:
1 0 1 2 3 4 5 6 7 8 9 A B C D E F
2 0 0 1 2 3 4 5 6 7 8 9 a b c d e f
3 1 10 11 12 13 14 15 16 17 18 19 1a 1b 1c 1d 1e 1f
4 2 20 21 22 23 24 25 26 27 28 29 2a 2b 2c 2d 2e 2f
5 3 30 31 32 33 34 35 36 37 38 39 3a 3b 3c 3d 3e 3f
6 4 40 41 42 43 44 45 46 47 48 49 4a 4b 4c 4d 4e 4f
7 5 50 51 52 53 54 55 56 57 58 59 5a 5b 5c 5d 5e 5f
8 6 60 61 62 63 64 65 66 67 68 69 6a 6b 6c 6d 6e 6f
9 7 70 71 72 73 74 75 76 77 78 79 7a 7b 7c 7d 7e 7f
10 8 80 81 82 83 84 85 86 87 88 89 8a 8b 8c 8d 8e 8f
11 9 90 91 92 93 94 95 96 97 98 99 9a 9b 9c 9d 9e 9f
12 a a0 a1 a2 a3 a4 a5 a6 a7 a8 a9 aa ab ac ad ae af
13 b b0 b1 b2 b3 b4 b5 b6 b7 b8 b9 ba bb bc bd be bf
14 c c0 c1 c2 c3 c4 c5 c6 c7 c8 c9 ca cb cc cd ce cf
15 d d0 d1 d2 d3 d4 d5 d6 d7 d8 d9 da db dc dd de df
16 e e0 e1 e2 e3 e4 e5 e6 e7 e8 e9 ea eb ec ed ee ef
17 f f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 fa fb fc fd fe ff
本文重点叙述步骤2的推导。
步骤二:
这里边有三个概念:有限域、GF(2^8)、逆。
有限域:我的理解是,有一些元素构成了一个集合,集合中的一个或多个元素,进行某种运算,所得的结果仍然是集合中的元素。 元素,可以是具体的数字,也可以是字母,或是表达式,等等;某种运算,可以是加减乘除,或者逻辑运算,或者求余,或者是这几种运算的组合,等等。 这个定义当然很不严格,但是我觉得对于理解这个S盒推导够用了。
GF(2^8):GF()是代表一个有限域,2^8=256,是指这个有限域内的元素的个数,即256个。
举个是有限域的集合的例子吧。
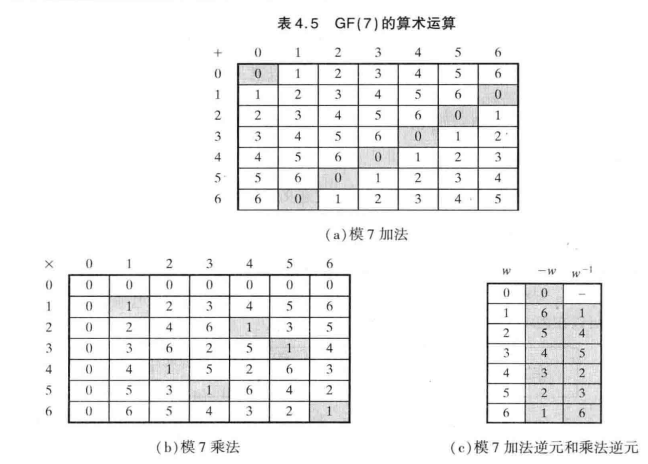
GF(7)={0,1,2,3,4,5,6},它是关于任意两个元素的相加/乘积模7运算的有限域。特点是任意两个元素相加/乘积,对7取余数,这个余数仍然在GF(7)内。
截取《密码编码学与网络安全--原理和实践》中的例子:
此外,这个GF(7)的7叫做阶,特点是阶与域内的元素都互素(互质)。
在计算机中,一个字节是8位,0~255刚好是一个字节所能代表的所有数字,但是呢,GF(256),256对于0~255内的元素并不是每个都互素(互质),当以251为模时,251~255又不能用,造成浪费,所以不能直接使用上边的计算形式。但是我们还得必须用0~255这256个整数作为一个集合,通过某种运算构成有限域,所有只能把研究重点放在“某种运算”上。可能是为了区分GF(256),所以用GF(2^8)。
逆:乘法逆元。定义:GF(p), (a)、(b)、(a-1)都在GF(p)内,其中(a)、(a-1)互为乘法逆元,则有:[(a) X (a-1)] mod p = 1;
第二个步骤,就是 在步骤一得到的数组基础上,对每个元素 在 GF(2^8)有限域上求解出乘法逆元,在原位置替换该元素。
如何求解有限域上的逆元?《密码编码学与网络安全--原理和实践》中从欧几里得算法开始做知识铺垫,到扩展欧几里得算法。我们可以得出求乘法逆元的一个程序上可实现的方法。
d=gcd(a,b),d是a和b的最大公约数,或者叫最大公因子。求解步骤:
1、定义变量:r0, r1, r2
2、赋初值r0=a;r1=b;
3、求解r0、r1的余数:r3=r0 Mod r1;
4、更新变量:r0=r1;r1=r2;
5、从3开始重复,一直到求解的余数r1是0结束。
6、r0就是要求解的最大公约数。
long gcd(long a, long b)
{
long tmp;
while(b)
{
tmp=a;
a=b;
b=tmp%b;
}
return a;
}
欧几里得算法的关键是gcd(a,b)=gcd(b,(a mod b));为什么能成立?
可以证明:
当a>b,就有,a=q1 * b + r1,r1 = a - q1 * b;
假设 d=gcd(a,b),那么d分别是a和b的最大公因子,记作:d|a,d|b,所以:d|(a-q1 * b)=d|r1
所以有d=gcd(b,r1)=gcd(b, (a mod b));
《密码编码学与网络安全--原理和实践》里边讲解会更详细:
扩展欧几里得算法的计算步骤同欧几里得算法的步骤相似,由一个公式迭代计算,一直达到某个条件成立结束迭代,返回结果。
扩展欧几里得算法用来求解乘法逆元,为什么?
上边已经有了公式:[(a) * (a-1)] mod p = 1;
可以等效变换成:p * x + 1 = (a) * (a-1)
========> - p * x + (a) * (a-1) = 1
与ax+by=1的形式是不是很像?
与ax+by=gcd(a,b)=1的形式是不是很像?
gcd(a,b)=1,就是a、b互素即可。
可以看出,可以运用欧几里得算法的步骤计算乘法逆元,但是怎么计算呢?
这点我还是照搬《密码编码学与网络安全--原理和实践》里边的讲解步骤吧,我觉得不会比他讲得更好了。
就是这样,初始条件:(R-1) = a; R0=b; (X-1)=1;X0=0;(Y-1)=0;Y0=1;
迭代步骤:Rn=(Rn-2) Mod (Rn-1);Qn = [(Rn-2) /(Rn-1)] {(Rn-2) /(Rn-1)的商};Xn = (Xn-2) - (Xn-2) ;Yn = (Yn-2) - (Yn-2) 。
终止条件:Rn=1时,计算出来的Yn即是结果。
如果结果为负数,需要加上模值变为正数。
代码如下:
long multiplicativeInverse(long a, long b)
{
long r0,r1,r2,q1,x0,x1,x2,y0,y1,y2; long d = gcd(a,b);
if((d!=1)&&(d!=-1))
{
printf("a、b不互质\r\n");
return -1;
} r0=a;
r1=b; x0=1;
y0=0; x1=0;
y1=1; if((b==1)||(b==-1))
{
y2=y1;
} while((r1!=1)&&(r1!=-1))
{
q1=r0/r1; r2=r0%r1; x2=x0-q1*x1;
y2=y0-q1*y1; r0=r1;
r1=r2; x0=x1;
x1=x2; y0=y1;
y1=y2;
} if(y2 < 0)
{
y2=a+y2;
} return y2;
}
回归到GF(2^8)有限域,需要找到“某种运算”,使GF(2^8)有限域成立。这种运算是多项式除法运算。
多项式如下形式:
我们可以把GF(2^8)有限域内的每一个元素,按照下列方式写成多项式的形式:
设 字节a ∈ GF(2^8),写成二进制的形式a=b7b6b5b4b3b2b1b0,用bn代表a的每一位,其中n是二进制数中的位置;
那么,bn当作系数,n作为变量x的指数;
可以把一个字节写成:

这种形式。
举例:
0x9A=(b)10011010,写成多项式形式:x^7+x^4+x^3+x。
多项式除法运算,计算规则:
1、遵循代数基本规则中的普通多项式运算规则;
2、系数运算遵循以2为模的加法和乘法运算;(原话是:系数运算以p为模,即遵循有限域Zp上的运算规则);
3、如果乘法运算的结果是次数大于7(原文:n-1)的多项式,那么必须将其除以某个次数为8(原文:n)的即约多项式m(x)并取余式,对于多项式f(x),这个余数可表示为:即r(x) = f(x) mod m(x)。
高级加密标准AES使用有限域GF(2^8)上的运算,其中即约多项式m(x)=x^8 + x^4 + x^3 + x + 1;
举例:
m(x)=x^8 + x^4 + x^3 + x + 1;
f(x) =x^6 + x^4 + x^2 + x + 1;g(x) =x^7 + x + 1;
f(x) * g(x) = (x^6 + x^4 + x^2 + x + 1) * (x^7 + x + 1)
= x^13 + x^11 + x^9 + x^8 + x^7
+ x^7 + x^5 + x^3 + x^2 + x
+ x^6 + x^4 + x^2 + x + 1
= x^13 + x^11 + x^9 + x^8 + x^6+ x^5 + x^4 + x^3 + 1
r(x) = [f(x) * g(x)] mod m(x) => m(x) * q(x) + r(x) = f(x) * g(x):
q(x) = x^5 + x^3;r(x) = x^7 + x^6 + 1。
上文已经讲到:扩展欧几里得算法用来求解乘法逆元。
(b-1)*b mod a = 1; => ax+by=1=gcd(a, b)
把a、b用多项式替代,形式如下:
b-1(x) * b(x) mod m(x) = 1 => m(x)v(x) + b(x)w(x) = 1 = gcd(m(x), b(x))
直接引用上边求乘法逆元的步骤,用多项式直接替代数值计算:
重述如下:
1、把带求解的字节变换成多项式形式b(x);
2、初始条件:
(R-1) = m(x); R0=b(x);
(v-1)(x)=1; v0(x)=0;
(w-1)(x)=0; w0(x)=1;
3、迭代步骤:
Rn(x)=(Rn-2)(x) Mod (Rn-1)(x);
Qn(x) = [(Rn-2)(x) / (Rn-1)(x)] 即:{(Rn-2) /(Rn-1)的商};
vn(x) = (vn-2)(x) - Qn(x)*(vn-2)(x) ;
wn(x) = (wn-2)(x) - Qn(x)*(wn-2) 。
4、终止条件:
Rn(x)=1时,计算出来的wn(x)即是结果多项式。
5、把wn(x)变换回字节。
上述步骤中,需要专门的多项式乘法、多项式除法、多项式求余运算的实现函数。
多项式乘法函数:
//GF(2^8)的多项式乘法
uint16_t polynomialMutil(uint8_t a, uint8_t b)
{
uint16_t tmp[]={};
uint8_t i;
for(i=;i<;i++)
{
tmp[i] = (a<<i)*((b>>i)&0x1);
} tmp[] = tmp[] ^ tmp[] ^ tmp[] ^ tmp[] ^ tmp[] ^ tmp[] ^ tmp[] ^ tmp[]; return tmp[];
}
多项式除法函数:
//找到最高位
uint8_t findHigherBit(uint16_t val)
{
int i=;
while(val)
{
i++;
val = val>>;
}
return i;
} //GF(2^8)的多项式除法
uint8_t gf28_div(uint16_t div_ed, uint16_t div, uint16_t *remainder)
{
uint16_t r0=;
uint8_t qn=;
int bitCnt=; r0=div_ed; bitCnt = findHigherBit(r0)-findHigherBit(div);
while(bitCnt>=)
{
qn = qn | (<<bitCnt);
r0 = r0 ^ (div<<bitCnt);
bitCnt = findHigherBit(r0)-findHigherBit(div);
}
*remainder = r0;
return qn;
}
多项式的扩展欧几里得算法:
//GF(2^8)多项式的扩展欧几里得算法
uint8_t extEuclidPolynomial(uint8_t a, uint16_t m)
{
uint16_t r0, r1, r2;
uint8_t qn, v0, v1, v2, w0, w1, w2; r0=m;
r1=a; v0=;
v1=; w0=;
w1=; while(r1!=)
{
qn=gf28_div(r0, r1, &r2); v2=v0^polynomialMutil(qn, v1);
w2=w0^polynomialMutil(qn, w1); r0=r1;
r1=r2; v0=v1;
v1=v2; w0=w1;
w1=w2;
}
return w1;
}
至此,S盒变换的第二步骤实现完成。
根据 扩展欧几里得算法,得到的中间状态的S盒如下:
A B C D E F
8d f6 cb 7b d1 e8 4f c0 b0 e1 e5 c7
b4 aa 4b 2b 5f 3f fd cc ff ee b2
3a 6e 5a f1 4d a8 c9 c1 a a2 c2
2c 6c f3 f2 6f bb
1d fe 2d f5 a7 ab e9
ed 5c ca 4c bf 3e f0 ec
5e af d3 a6 f4 df 3b
b7 b5 ba 3c b6 d0 a1 fa
7e 7f be 9b 9e d9 f7 b9 a4
de 6a 6d d8 8a 2a 9f f9 dc 9a
a fb 7c 2e c3 8f b8 c8 4a ce e7 d2
b c e0 1f ef a5 8e 3d bd bc
c b 2f a3 da d4 e4 f a9 1b fc ac e6
d 7a ae c5 db e2 ea 8b c4 d5 9d f8 6b
e b1 d d6 eb c6 e cf ad 4e d7 e3 5d 1e b3
f 5b 8c dd 9c 7d a0 cd 1a 1c
步骤三:S盒字节变换和逆S盒字节变换:
//S盒字节变换
uint8_t byteTransformation(uint8_t a, uint8_t x)
{
uint8_t tmp[]={}; for(uint8_t i=;i<;i++)
{
tmp[i]= (((a>>i)&0x1)^((a>>((i+)%))&0x1)^((a>>((i+)%))&0x1)^((a>>((i+)%))&0x1)^((a>>((i+)%))&0x1)^((x>>i)&0x1)) << i;
}
tmp[] = tmp[]+tmp[]+tmp[]+tmp[]+tmp[]+tmp[]+tmp[]+tmp[];
return tmp[];
} //逆S盒字节变换
uint8_t invByteTransformation(uint8_t a, uint8_t x)
{
uint8_t tmp[]={}; for(uint8_t i=;i<;i++)
{
tmp[i]= (((a>>((i+)%))&0x1)^((a>>((i+)%))&0x1)^((a>>((i+)%))&0x1)^((x>>i)&0x1)) << i;
}
tmp[] = tmp[]+tmp[]+tmp[]+tmp[]+tmp[]+tmp[]+tmp[]+tmp[];
return tmp[];
}
S盒变换代码:
//S盒产生
void s_box_gen(void)
{
uint8_t i,j;
uint8_t s_box_ary[][] = {}; //初始化S盒
for(i=;i<0x10;i++)
{
for(j=;j<0x10;j++)
{
s_box_ary[i][j] = ((i<<)&0xF0) + (j&(0xF));
}
} printf(" 0 1 2 3 4 5 6 7 8 9 A B C D E F");
for(i=;i<0x10;i++)
{
printf("\r\n%2x",i);
for(j=;j<0x10;j++)
{
printf(" %2x",s_box_ary[i][j]);
}
}
//求在GF(2^8)域上的逆,0映射到自身
printf("\r\n");
for(i=;i<0x10;i++)
{
for(j=;j<0x10;j++)
{
if(s_box_ary[i][j] != )
{
s_box_ary[i][j] = extEuclidPolynomial(s_box_ary[i][j],0x11B);
}
}
} printf("\r\n\r\n 0 1 2 3 4 5 6 7 8 9 A B C D E F");
for(i=;i<0x10;i++)
{
printf("\r\n%2x",i);
for(j=;j<0x10;j++)
{
printf(" %2x",s_box_ary[i][j]);
}
}
//对每个字节做变换
for(i=;i<0x10;i++)
{
for(j=;j<0x10;j++)
{
s_box_ary[i][j]=byteTransformation(s_box_ary[i][j], 0x63);
}
} printf("\r\n\r\n 0 1 2 3 4 5 6 7 8 9 A B C D E F");
for(i=;i<0x10;i++)
{
printf("\r\n%2x",i);
for(j=;j<0x10;j++)
{
printf(" %2x",s_box_ary[i][j]);
}
}
}
输出如下:
A B C D E F
a b c d e f
1a 1b 1c 1d 1e 1f
2a 2b 2c 2d 2e 2f
3a 3b 3c 3d 3e 3f
4a 4b 4c 4d 4e 4f
5a 5b 5c 5d 5e 5f
6a 6b 6c 6d 6e 6f
7a 7b 7c 7d 7e 7f
8a 8b 8c 8d 8e 8f
9a 9b 9c 9d 9e 9f
a a0 a1 a2 a3 a4 a5 a6 a7 a8 a9 aa ab ac ad ae af
b b0 b1 b2 b3 b4 b5 b6 b7 b8 b9 ba bb bc bd be bf
c c0 c1 c2 c3 c4 c5 c6 c7 c8 c9 ca cb cc cd ce cf
d d0 d1 d2 d3 d4 d5 d6 d7 d8 d9 da db dc dd de df
e e0 e1 e2 e3 e4 e5 e6 e7 e8 e9 ea eb ec ed ee ef
f f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 fa fb fc fd fe ff A B C D E F
8d f6 cb 7b d1 e8 4f c0 b0 e1 e5 c7
b4 aa 4b 2b 5f 3f fd cc ff ee b2
3a 6e 5a f1 4d a8 c9 c1 a a2 c2
2c 6c f3 f2 6f bb
1d fe 2d f5 a7 ab e9
ed 5c ca 4c bf 3e f0 ec
5e af d3 a6 f4 df 3b
b7 b5 ba 3c b6 d0 a1 fa
7e 7f be 9b 9e d9 f7 b9 a4
de 6a 6d d8 8a 2a 9f f9 dc 9a
a fb 7c 2e c3 8f b8 c8 4a ce e7 d2
b c e0 1f ef a5 8e 3d bd bc
c b 2f a3 da d4 e4 f a9 1b fc ac e6
d 7a ae c5 db e2 ea 8b c4 d5 9d f8 6b
e b1 d d6 eb c6 e cf ad 4e d7 e3 5d 1e b3
f 5b 8c dd 9c 7d a0 cd 1a 1c A B C D E F
7c 7b f2 6b 6f c5 2b fe d7 ab
ca c9 7d fa f0 ad d4 a2 af 9c a4 c0
b7 fd 3f f7 cc a5 e5 f1 d8
c7 c3 9a e2 eb b2
2c 1a 1b 6e 5a a0 3b d6 b3 e3 2f
d1 ed fc b1 5b 6a cb be 4a 4c cf
d0 ef aa fb 4d f9 7f 3c 9f a8
a3 8f 9d f5 bc b6 da ff f3 d2
cd c ec 5f c4 a7 7e 3d 5d
4f dc 2a ee b8 de 5e b db
a e0 3a a 5c c2 d3 ac e4
b e7 c8 6d 8d d5 4e a9 6c f4 ea 7a ae
c ba 2e 1c a6 b4 c6 e8 dd 1f 4b bd 8b 8a
d 3e b5 f6 e b9 c1 1d 9e
e e1 f8 d9 8e 9b 1e e9 ce df
f 8c a1 d bf e6 2d f b0 bb
逆S盒变换代码:
//逆S盒产生
void inv_s_box_gen(void)
{
uint8_t i,j;
uint8_t s_box_ary[][] = {};
uint8_t b=, bb=; //初始化S盒
for(i=;i<0x10;i++)
{
for(j=;j<0x10;j++)
{
s_box_ary[i][j] = ((i<<)&0xF0) + (j&(0xF));
}
} printf(" 0 1 2 3 4 5 6 7 8 9 A B C D E F");
for(i=;i<0x10;i++)
{
printf("\r\n%2x",i);
for(j=;j<0x10;j++)
{
printf(" %2x",s_box_ary[i][j]);
}
}
//对每个字节做变换
for(i=;i<0x10;i++)
{
for(j=;j<0x10;j++)
{
s_box_ary[i][j]=invByteTransformation(s_box_ary[i][j], 0x05);
}
} printf("\r\n\r\n 0 1 2 3 4 5 6 7 8 9 A B C D E F");
for(i=;i<0x10;i++)
{
printf("\r\n%2x",i);
for(j=;j<0x10;j++)
{
printf(" %2x",s_box_ary[i][j]);
}
} //求在GF(2^8)域上的逆,0映射到自身
printf("\r\n");
for(i=;i<0x10;i++)
{
for(j=;j<0x10;j++)
{
if(s_box_ary[i][j] != )
{
s_box_ary[i][j] = extEuclidPolynomial(s_box_ary[i][j],0x11B);
}
}
} printf("\r\n\r\n 0 1 2 3 4 5 6 7 8 9 A B C D E F");
for(i=;i<0x10;i++)
{
printf("\r\n%2x",i);
for(j=;j<0x10;j++)
{
printf(" %2x",s_box_ary[i][j]);
}
}
}
输出如下:
A B C D E F
a b c d e f
1a 1b 1c 1d 1e 1f
2a 2b 2c 2d 2e 2f
3a 3b 3c 3d 3e 3f
4a 4b 4c 4d 4e 4f
5a 5b 5c 5d 5e 5f
6a 6b 6c 6d 6e 6f
7a 7b 7c 7d 7e 7f
8a 8b 8c 8d 8e 8f
9a 9b 9c 9d 9e 9f
a a0 a1 a2 a3 a4 a5 a6 a7 a8 a9 aa ab ac ad ae af
b b0 b1 b2 b3 b4 b5 b6 b7 b8 b9 ba bb bc bd be bf
c c0 c1 c2 c3 c4 c5 c6 c7 c8 c9 ca cb cc cd ce cf
d d0 d1 d2 d3 d4 d5 d6 d7 d8 d9 da db dc dd de df
e e0 e1 e2 e3 e4 e5 e6 e7 e8 e9 ea eb ec ed ee ef
f f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 fa fb fc fd fe ff A B C D E F
4f db 2c b8 f2 1d c3 7e ea a0
a1 eb 7f c2 1c f3 b9 2d da 4e
4c d8 2f f1 bb 1e 8a c0 7d a3 e9
e8 a2 7c c1 8b 1f ba f0 2e d9 4d
dd be f4 2a c5 8f 1b ec a6
a7 ed 1a 8e c4 2b f5 bf dc
de 4a f7 bd 8c c6 a5 ef 7b
7a ee a4 c7 8d bc f6 4b df
6a b4 fe 9d d7 e6 ac 5b cf
ce 5a ad e7 d6 9c ff b5 6b
a fd b7 a d4 9e 3b af e5 cc
b cd e4 ae 3a 9f d5 b b6 fc
c b2 f8 6c 9b d1 f e0 aa 3e c9 5d
d 5c c8 3f ab e1 e d0 9a 6d f9 b3
e fb b1 6f d2 c a9 e3 3d ca 5e
f 5f cb 3c e2 a8 d d3 6e b0 fa A B C D E F
6a d5 a5 bf a3 9e f3 d7 fb
7c e3 9b 2f ff 8e c4 de e9 cb
7b a6 c2 3d ee 4c b fa c3 4e
2e a1 d9 b2 5b a2 6d 8b d1
f8 f6 d4 a4 5c cc 5d b6
6c fd ed b9 da 5e a7 8d 9d
d8 ab 8c bc d3 a f7 e4 b8 b3
d0 2c 1e 8f ca 3f f c1 af bd 8a 6b
3a 4f dc ea f2 cf ce f0 b4 e6
ac e7 ad e2 f9 e8 1c df 6e
a f1 1a 1d c5 6f b7 e aa be 1b
b fc 3e 4b c6 d2 9a db c0 fe cd 5a f4
c 1f dd a8 c7 b1 ec 5f
d 7f a9 b5 4a d 2d e5 7a 9f c9 9c ef
e a0 e0 3b 4d ae 2a f5 b0 c8 eb bb 3c
f 2b 7e ba d6 e1 c 7d
以上代码肯定不是最优代码,欢迎拍砖,并在留言区留下您宝贵意见,谢谢!
AES128加密-S盒和逆S盒构造推导及代码实现的更多相关文章
- AES加密的S盒和逆S盒的推导代码备份(C实现)
摘取自https://www.cnblogs.com/Junbo20141201/p/9369860.html,感谢原作者的详细解读. #include <stdio.h> ][] = { ...
- 标准盒模型与IE盒模型之间的转换
首先上图,这两张很明显可以看出IE盒模型和标准盒模型之间的差别. 当然今天不是去细细追究两种模型具体是怎么去计算布局的,那个很多文章已经已经有过了,不再重复.以前刚开始学习盒模型的时候,就学到的是IE ...
- IE盒模型与W3C盒模型区别
前两天被人问到,叫我解释一下标准盒模型与IE盒模型,额,当时只能说,知道一点,但是没有深入的去探讨过,所以下来之后就自己写了例子,亲自去验证并且查看了网上的一些资料,现将其整理如下: 一.css盒模型 ...
- IE盒模型和标准盒模型
标准盒模型和ie盒模型(怪异盒模型) w3c标准盒模型 width和height不包括padding和border ie盒模型 width和height包含padding和border ie8以上都是 ...
- 使用AES128加密字符串
import lombok.extern.slf4j.Slf4j; import org.apache.commons.codec.binary.Base64; import org.apache.c ...
- seccomp沙盒逃逸基础——沙盒的规则编写
seccomp沙盒逃逸基础--沙盒的规则编写 引入: 安全计算模式 seccomp(Secure Computing Mode)是自 Linux 2.6.10 之后引入到 kernel 的特性.一切都 ...
- boxsizing属性 IE盒模型和标准盒模型
CSS3有一个非常有用但应用不广泛的属性: box-sizing: content-box | border-box | inherit content-box,默认属性,遵从标准盒模型. borde ...
- IOS 学习之 iOS沙盒(sandbox) 介绍 沙盒机制 文件操作(一)
1.iOS沙盒机制 iOS应用程序只能在为该改程序创建的文件系统中读取文件,不可以去其它地方访问,此区域被成为沙盒,所以所有的非代码文件都要保存在此,例如图像,图标,声音,映像,属性列表,文本文件等. ...
- 大前端学习笔记整理【一】CSS盒模型与基于盒模型的6种元素居中方案
概览 CSS盒模型,规定了元素框来处理元素的 内容.内边距.边框和外边距的方式 元素部分是指内容部分,也是最实际的内容,包围内容的称之为内边距,内边距外围是边框,边框外围就是外边距:且外边距是透明的, ...
随机推荐
- PHP:使用php,循环html中的select标签与Php数据
select标签,我们都知道是下拉列表,这里,我们使用foreach循环,将select中的数据进行输出 例子: 1.数据表:mimi_article,表中有个字段,为1或0,表示着是或否 2.通过p ...
- Orchard Core 文档翻译 (三) Orchard Core Modules
原文连接:https://www.cnblogs.com/Qbit/p/9746442.html 转载请注明出处 介绍 Orchard Core Modules库提供了一种机制,可以拥有一个独立的模块 ...
- C++设计模式实现--訪问者(Visitor)模式
版权声明:本文为博主原创文章,未经博主同意不得转载. https://blog.csdn.net/L_Andy/article/details/36896645 一. 訪问者模式 定义:表示一个作用于 ...
- POJ 2195 Going Home 【二分图最小权值匹配】
传送门:http://poj.org/problem?id=2195 Going Home Time Limit: 1000MS Memory Limit: 65536K Total Submis ...
- (第三场) C Shuffle Cards 【STL_rope || splay】
题目链接:https://www.nowcoder.com/acm/contest/141/C 题目描述 Eddy likes to play cards game since there are a ...
- 访问XML文件中的信息
- 【转】异步的AsyncHttpClient使用详解
http://blog.csdn.net/angjunqiang/article/details/55259170 背景 前面的一篇文章[同步的HttpClient使用详解]中,提到了服务端通进行网络 ...
- git上传过滤忽略文件
有些时候我们不想把某些文件纳入版本控制中,比如数据库文件,临时文件,设计文件等 在主目录下建立".gitignore"文件,此文件有如下规则: 忽略文件中的空行或以井号(#)开始的 ...
- 解决:fontawesome-webfont.woff2?v=4.6.3 404 (Not Found)
用Bootstrap里面的字体,你项目中会报一个错,一个字体找不到,但我们的项目中却是存在这个字体的. 解决方法: 修改我们的Web.Config文件
- SpringBoot非官方教程 | 第十三篇:springboot集成spring cache
转载请标明出处: 原文首发于:https://www.fangzhipeng.com/springboot/2017/07/11/springboot13-springcache/ 本文出自方志朋的博 ...