FPGA算法学习(1) -- Cordic（圆周系统之向量模式）

旋转模式用来解决三角函数，实现极坐标到直角坐标的转换，基础理论请参考Cordic算法——圆周系统之旋转模式。那么，向量模式则用来解决反三角函数的问题，体现的应用主要是直角坐标向极坐标转换，即已知一点的直角坐标(x,y)，求其极坐标(α,γ)，实际上是求arctan(y/x)。

旋转模式下，每次迭代使z趋近于α（α-z趋近于0），而向量模式下，则使y趋近于0，这一点很好理解，即从坐标位置，旋转到x正半轴，一共旋转了多少角度，则该角度即为α，从而知道了极角。

如图所示，在单位圆上，向量OP与X轴的正半轴夹角为α，故P点的坐标可表示为

根据开头描述，我们需要转动向量OP，先顺时针旋转θ角至向量OQ，Q点的坐标可表示为

这里定义θ为目标旋转角度。根据三角函数公式可将上式展开为

现在已经有点 Cordic 算法的样子了，但是我们看到每次旋转都要计算 4 次浮点数的乘法运算，运算量还是太大了。还需要进一步的改进，改进的切入点当然还是坐标变换的过程。

将式(1.1)代入到式(1.3)中可得

用矩阵形式表示为：

旋转了i次以后，可以得到：

最终需将y_Q_i+1转为0，先按45°的二分法查找来解释过程，用C语言描述过程为：

#include <stdio.h>
#include <stdlib.h>

double cordic_v(double x, double y);

int main(viod)
{
	double alfa = cordic_v(120.0,200.0);		//直角坐标（x,y）
	printf("\n 极角为 = %f \n",alfa);
	return 0;
}
double cordic_v(double x, double y)
{
	const double sine[] = {0.7071067811865,0.3826834323651,0.1950903220161,
						0.09801714032956,0.04906767432742,0.02454122852291,0.01227153828572,
						0.006135884649154,0.003067956762966,0.001533980186285,
						7.669903187427045e-4,3.834951875713956e-4,1.917475973107033e-4,
						9.587379909597735e-5,4.793689960306688e-5,2.396844980841822e-5
						};

	const double cosine[] = {0.7071067811865,0.9238795325113,0.9807852804032,0.9951847266722,
							0.9987954562052,0.9996988186962,0.9999247018391,0.9999811752826,0.9999952938096,
							0.9999988234517,0.9999997058629,0.9999999264657,0.9999999816164,0.9999999954041,
							0.999999998851,0.9999999997128
						};
	int i = 0;
	double x_new, y_new;
	double angleSum = 0.0;
	double angle = 45.0;		//第一次旋转角度为45°
	for( i=0; i<15;i++)
	{
		if(y > 0)
		{
			x_new = x * cosine[i] + y * sine[i];
			y_new = y * cosine[i] - x * sine[i];
			x = x_new;
			y = y_new;
			angleSum += angle;
		}

		else
		{
			x_new = x * cosine[i] - y * sine[i];
			y_new = y * cosine[i] + x * sine[i];
			x = x_new;
			y = y_new;
			angleSum -= angle;
		}
		printf("旋转次数: i = %2d 旋转角度 = %10f, 累计旋转角度 = %10f\n", i+1, angle,angleSum );
		angle /= 2;
	}
	return angleSum;
}

经过旋转模式的推导，向量模式的伪旋转公式，可表示为

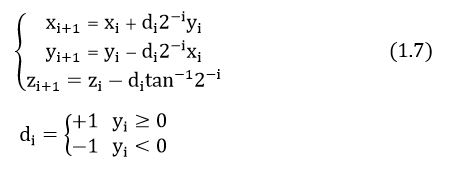
C语言描述过程，如下：

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

double cordic_v(double x, double y);
double r = 0.0;	//定义一个模长全局变量		

int main(viod)
{
	double alfa = cordic_v(120.0,200.0);		//直角坐标（x,y）
	printf("\n极角 = %5f, 模长 = %5f\n",alfa,r);
	return 0;
}
double cordic_v(double x, double y)
{
	const double theta[] = { 45.0, 26.56505118, 14.03624347, 7.125016349,
						3.576334375, 1.789910608, 0.8951737102, 0.4476141709,
						0.2238105004, 0.1119056771, 0.05595289189, 0.02797645262,
						0.01398822714, 0.006994113675, 0.003497056851, 0.001748528427
						}; //旋转角度
	int i = 0;
	double x_new, y_new;
	double angleSum = 0.0;
	r = sqrt(x*x+y*y);
	for( i=0; i<16;i++)
	{
		if(y > 0)
		{
			x_new = x + y/(1<<i);
			y_new = y - x/(1<<i);
			x = x_new;
			y = y_new;
			angleSum += theta[i];
		}

		else
		{
			x_new = x - y/(1<<i);
			y_new = y + x/(1<<i);
			x = x_new;
			y = y_new;
			angleSum -= theta[i];
		}
		printf("旋转次数: i = %2d 旋转角度 = %10f, 累计旋转角度 = %10f, y = %5f\n", i+1,theta[i],angleSum,y );
	}
	return angleSum;
}

同样，向量模式的cordic算法适用于第一、四象限的坐标变换，在第二、三象限的坐标需要进行预处理。

参考

• 三角函数计算，Cordic 算法入门--Ivan

• 《基于FPGA的数字信号处理（第2版）》——高亚军著