SPFA解决单源最短路径

SPFA(Shortest Path Faster Algorithm):

一:基本算法

　　在求解单源最短路径的时候,最经典的是 Dijkstra 算法,但是这个算法对于含有负权的图就无能为力了,而 Bellman - Ford 算法的复杂度又过于高,这时 SPFA就应运而生了. SPFA 在 Bellman - Ford 算法的基础上进行了改进,使其能够在计算带有负权的图的单源最短路径的基础上,时间复杂度大幅降低.

　　众所周知 Bellman -Ford 算法会对每条边进行 n - 1 次检查,但是在这些检查过程中,有许多检查是没有必要的.事实上,唯一应该检查的边存在一个特点:这些边的起点在上一次处理时到源点的距离发生了变化,即松弛成功的边的终点.既然如此,那么就可以对算法进行优化,即每遍只处理特殊的点,这些点是上一次在松弛过程中某条边的终点.设立一个先进先出的队列来维护这些待处理的点,优化时每次取出队首节点 u, 并且对所有从点 u 出发的边进行松弛操作,对于每条边的终点 v,如果以点 v 为终点的边松弛成功, 且 v 不在队列内, 就将点 v 加入队尾.这样不断从对列取出节点来进行松弛操作,直至队列空为止.这个算法保证只要最短路径存在, SPFA 必定能求出最小值.

　　SPFA同样可以判断负环,如果某个点弹出队列的次数超过 N - 1 次,则存在负环.对于存在负环的图,是无法计算出单源最短路径的.

二:伪代码

　　在以下说明中, inque[] 记录点是否在队列中, 使用链式前向星存图, 结果保留在 dist[] 中.

　　(1):初始化,源的距离 dist[s] 设为 0, 其他点的距离设置为 INF, 新建一个队列, 将源点 s 入队, 标记源点 s 已经在对列中.

　　(2):从队首取出一个点 top, 标记top出队, top 出队的次数加 1,并对这个次数检查, 如果大于 n, 说明出现负环, 结束算法. 否则遍历从点 top 出发的边, 如果边 k 的终点 to 的 dist[] 可以更新, 即 dist[ edge[k].to ] > dist[top] + edge[k].w, 则更新 dist[ edge[k].to ] = dist[top] + edge[k].w, 检查 to 是否在队列内, 如果不在则加入队列.

　　(3)重复执行步骤(2), 直至队列为空.

三:以图为列

初始化队列、图和 dist[] 数组:

1.选择队列首部的点 “5”,对从此点出发的边 <"5", "3"> 和  <"5", "4"> 进行松弛:

2.选择队列首部的点 “3”,对从此点出发的边 <"3", “4”> 进行松弛, 松弛失败, 点 ”4“ 不会再次加入队列:

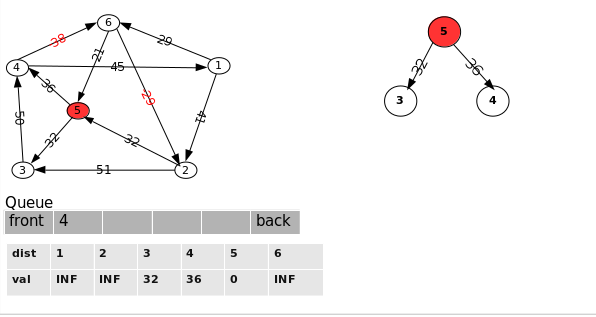
3.选择队列首部的点 “4”,对从此点出发的边 <"4", "1"> 和 <"4", "6">进行松弛:

4.选择队列首部的点 “1”,对从此点出发的边 <"1", '2"> 和 <"1", "6">进行松弛, 这里点”6“已经在队列内了,所以点 “6” 不会加入队列.

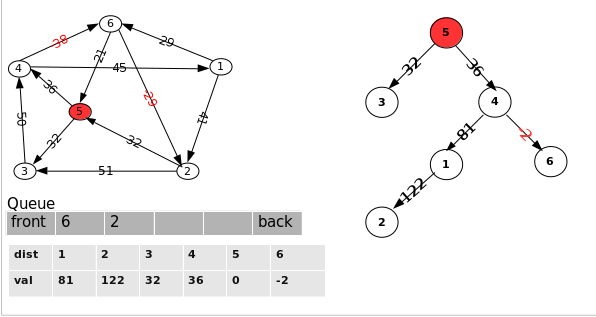
5.选择队列首部的点 “6”,对从此点出发的边<"6", "2"> 和 <"6", "5"> 进行松弛,.对边 <"6", "5"> 松弛失败, 虽然点 “5” 不在队列内, 但也不应该加入队列.

6.选择队列首部的点 “2”,对从此点出发的边<"2", "3"> 和 <"2", "5"> 进行松弛,.对边 <"2", "5"> 松弛失败, 点 “5” 不应该加入队列.

7.选择队列首部的点 “3”,对从此点出发的边<"3", "4"> 进行松弛,.且对边 <"3", "4"> 松弛失败, 此时队列为空算法结束.

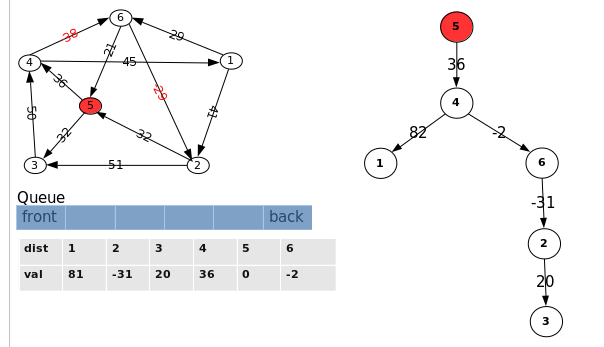
四:代码

 const int MAXN = ;
 const int MAXE = ;
 const int INF = INT_MAX;
 int dist[MAXN + ];// dist[i] 表示点 i 到源点 s 的最短距离

 int head[MAXN + ];//链式前向星存图
 struct NODE { int to; int w; int next; };
 NODE edge[MAXE];

 bool SPFA(int n, int s) {//s 为源点 n 为总的点数
     for(int i = ; i <= n; i++) dist[i] = INF;//初始化
     dist[s] = ;
     queue<int> rex;//保存待优化的节点
     rex.push(s);//从源点 s 开始优化s
     bool inque[MAXN + ] = { false };//inque[i] = false 表示点 i 在队列内
     inque[s] = true;
     int outque[MAXN + ] = {  };//记录每个点出对列的次数
     while(!rex.empty()) {
         int top = rex.front();//取队首的点为待拓展节点
         rex.pop();
         inque[top] = false;
         outque[top] ++;
         if(outque[top] > n) return false;//存在负环
         for(int k = head[top]; k != -; k = edge[k].next) {//对从当前点出发的所有边进行松弛操作
             if(dist[top] != INF && dist[ edge[k].to ] > dist[top] + edge[k].w) {
                 dist[ edge[k].to ] = dist[top] + edge[k].w;
                 if(!inque[ edge[k].to ]) {//如果当前边另外一端的顶点不在队列内,则加入到队尾
                     rex.push( edge[k].to );
                     inque[ edge[k].to ] = true;
                 }
             }
         }
     }
     return true;
 }

参考书籍 <<图论及应用>> 和网上部分资料.