五一清北学堂培训之Day 3之DP

今天又是长者给我们讲小学题目的一天

长者的讲台上又是布满了冰红茶的一天

-------------------------------------------------------------------------------------------------------------------------------------

正片开始

动态规划

动态规划是个抽象的东西。

接下来的例子小部分可能会比较搞笑

我们先来看一个严肃的例子，来认识一下什么是DP：

斐波那契数列：

大家都知道斐波那契数列是个啥吧

就是这个：    f(0)=0,f(1)=1,f(n)=f(n-1)+f(n-2)

它和DP有什么关系呢？

1.都要有边界条件（这里就是f(0)=0,f(1)=1）

2.都有转移方程（这里的是f(n)=f(n-1)+f(n-2)）

3.都有当前状态（这里就是f(n)）

这样我们也就总结出来了做DP要注意的东西：

1.定义状态

2.定义边界

3.转移方程

以上也是做DP的步骤。

代码的几种写法：

顺着推，逆着推，记忆化搜索

//以斐波那契数列为例的三种写法
int dfs(int n)
{   if(n==)f[]=;
    else if(n==)f[]=;
    if(vis[n])return f[n];
    vis[n]=true;
    f[n]=dfs(n-)+dfs(n-);
    return f[n];
}
int main()
{int n,f[];
  //逆着推（无优化）
  vis[]=;vis[]=;
  cin>>n;
  f[]=;
  f[]=;
  for(int i-;i<=n;i++)
    f[i]=f[i-]+f[i-];
  cout<<f[n];

//顺着推
 cin>>n;
 f[]=;f[]=;
  for(int i=;i<n;i++)
  {f[i+]+=f[i];
   f[i+]+=f[i];
  }
  //记忆化搜索
  cin>>n;
  cout<<dfs(n)<<endl;

}

noip的考纲虽然比宇宙还大，但是总会有那么几种常考的东西。

常考DP:

数位DP

树形DP

区间DP

状压DP

其它DP（这个是最常考的）

一.数位DP

  举个栗子

读入两个正整数l,r,求从l到r之间一共有多少个数？

ans=r-l+1

但是只有这么一句不优雅，所以我们要用数位DP做。

ans=[0,r]的数-[0,l]的数

这样我们就把问题转化为求[0,x]区间上的数了。我们先把x的十进制表示出来。

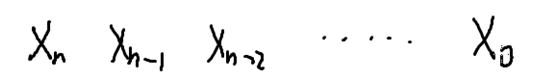
其中X0代表个位，X1代表十位.....以此类推

我们这个题实际上是求满足0<=v<=x的v

我们对v进行相同的操作

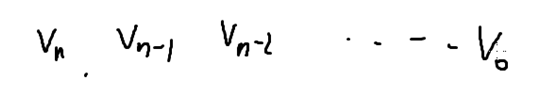
如果当v不足n位时，就是有前导0.我们在每一位上填上0~9之间的一个整数，看满足要求的v有多少。我们从高位开始填。那这就会有很多种情况对不对？我们举个例子分析一下

假如我们要填Vn-3,那么按照从高位开始填的顺序，Vn,Vn-1,Vn-2已经填好了。我们把每个Vi和每个Xi比较一下。

我们把这些数分到两边。

①.左边>右边   那Vn-3就随便填了

②.左边<右边   填的Vn-3就必须<=Xn-3,当然这里还有个坑，我们待会程序里讲

我们用f[i][j]表示已经填到了第i位，j表示V的第i-1位及以前是否等于X的i-1位及以前，这种情况下的方案数。（0是不等于，1是等于），ans=f[0][0]+f[0][1]。

转移：对于每个f[i][0],f[i][0]=9*f[i-1][0]+(X(n-i)-1)*f[i-1][1](后面这一部分是指前i-1位都等于，第i位不等于)

f[i][1]=f[i-1][1]，因为永远等于x的数不会变

边界：f[n+1][1]=1 因为Vn+1=Xn+1=0

int f[][];
int solve(int x)
{
    int z[];
    int n;
    while(x)
    {z[n++]=x%;
     x/=;
    }
    n--;
    memset(f,,sizeof(f));//要记住清空以防意外
    f[n+][]=;//Xn+1与Vn+1都是0，所以是等于（顶上界）的情况
    for(int i=n;i>;i--)
       for(int j=;j<=;j++)
         {
             if(j==)
              {
                  for(int k=;k<=;k++)
                  f[i][]+=f[i+][j];//把f[i][j]的方案数加到f[i][0]上 （注意不是+9） 用循环的方式加起来方便以后改程序
             }
             else
             {
                  for(int k=;k<=z[i];k++)
                  {if(k==z[i])f[i][]+=f[i+][j];//如果顶上界，就加到f[i][1]（顶上界的数组)（左边=右边）里面
                   else f[i][]+=f[i+][j];//如果当前位填的数<z[i]，就说明不顶上界，就加到f[i][0]里面
                  }
             }
         }
    return f[][]+f[][];
}
int main()
{int l,r;
    cin>>l>>r;
    cout<<solve(r)-solve(l-)<<endl;
}

上面说的顶上界就是Vi=Xi的情况（私下的称呼，懒的改了）

绕了好大一圈解决了一个简单题

数位之和：例如123，数位之和=1+2+3=6

这里把上一个题改一改，再加一个数组记录数位之和即可（i,j的意义不变）

int f[][];//方案数之和，j=0:不顶上界，j=1:顶上界
int g[][];//数位之和
int solve(int x)
{
    int z[];
    int n;
    while(x)
    {z[n++]=x%;
     x/=;
    }
    n--;
    memset(f,,sizeof(f));
    memset(g,,sizeof(g));
    f[n+][]=;
    g[n+][]=;
    for(int i=n;i>;i--)
       for(int j=;j<=;j++)
         {
             if(j==)
              {
                  for(int k=;k<=;k++)//枚举每个要填的数
                  {f[i][]+=f[i+][j];//每一个方案的后面都+k，那对总的数位之和的贡献就是f[i+1][j]（方案数)*k（新填的数)
                   g[i][]+=g[i+][j]+f[i+][j]*k
                  }
             }
             else
             {
                  for(int k=;k<=z[i];k++)
                  {if(k==z[i])
                  {f[i][]+=f[i+][j];
                  g[i][]+=g[i+][j]+f[i+][j]*k;
                  }
                   else
                   {f[i][]+=f[i+][j];
                    g[i][]+=g[i+][]+f[i+][j]*k;
                   }
             }
          }
         }
    return f[][]+f[][];
}
int main()
{int l,r;
    cin>>l>>r;
    cout<<solve(r)-solve(l-)<<endl;
}

这个题多了一个限制条件。

多加一个维度肯定能把这题做出来。

-------------------长者

那我们就多加一个维度好了。

状态：因为我们要比较相邻两个数位上的数，又是从高位向低位填写，所以只需要记录当前填的最后一位。

作业1：洛谷P2657windy数（咕咕咕）

树形DP：

我们看一道简单的不行的题

给定一棵有n个点的树，请问这棵树有几个点？

答案是n个点吗？真的是n个点吗？当然是啦

好我们想想这题怎么做

先介绍一下树。

树最上面的点叫根，最下面的点叫叶子结点。

子树：由一个结点向下走，能走到的所有结点构成的树叫以这个结点为根的子树。

有多少个点：以根节点为根的子树的点。f[i]:以i这个点为根的子树的点的个数，这里就要求f[1]。

边界：f[叶子结点]=1

转移：f[p]=f[ls[p]]+f[rs[p]]+1.左儿子+右儿子+1=p结点的子树大小

长者只放了伪代码qwq

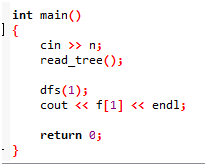
对了这个题的答案是n,所以这个题只要读入n,再输出就好辣。

我们来看点有档次的东西

给一个n个点的树，求直径（距离最远的两个点的距离）

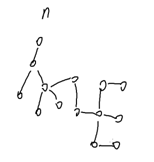
首先，每种路径都长这个样子（这里指一个点到另一个点）

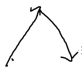
我们把它换个方向

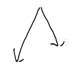
是不是顺眼了？这样就符合从一个结点向下走的方向了。

既然每种路径都长这样，那直径一定长这样喽。

从一个点找两种尽量长（最长+次长）的路径拼起来就是以这个点为拐点的最长一条路径。

我们用f[i][0]表示从点i向下走，最长的路径长度，f[i][1]表示从点i向下走，次长路径的长度。

状态转移便是选择儿子。

f[p][0]=max{f[p1][0],f[p2][0]...f[pk][0]}+1求最大值：必定走儿子中路线最长的那个，再加上1（用一 步到达儿子）

f[p][1]:假如我们刚才选了pi,f[p][1]=max{f[p1][0],...(把f[pi][0],f[pi][1]去掉)}+1

ans=f[1][0]+f[1][1];

状压DP

状压就是状态压缩。

为什么要状态压缩呢？

看个例子：

给n个点，坐标分别为(x1,y1),(x2,y2).........(xn,yn)（这不是个图，你可以乱走）一个人在一号点，从1号点出发，把剩下的点至少走一次，使走过的路径最短（TSP问题（中文：旅行商问题））

经典的Np-hard问题（最快也是2^n级别）

1.每个点只去一次

2.最短就是走线段

假如我们已经走了1，2，5

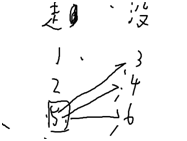
3,4,6每个点都可行。（只是不一定最短）

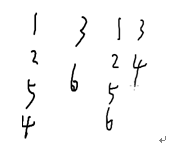
这里每个走过/没走过都是集合,so我们怎么表是成数组下标？

这里就是状态压缩了（集合--->数）。用二进制即可完成。

构造n位（元素的个数）二进制数，每位用0/1来表示某个元素是否在集合里。（0为不在，1为在）

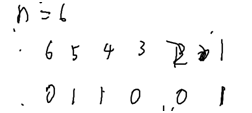
例如这个二进制数与{1,4,5}等价.

TSP问题：f[s][i],s为n位二进制数，(已经走过的点所对应的集合)已经走过s里的所有点,现在停留在i点的最小距离。

边界：f[1][1]=0.

枚举要走的点j。（要保证j不属于s这个集合）

--->f[ { s∪j } ][ j ]=f[ s ][ j ]+dis[ i ][ j ]（从点i走到点j）

转移：实际上是把走过的点的元素变多==>把二进制上的0不断边1==>s变大

所以按s从小到大枚举

 //状压dp
 int n,f[],x[],y[];
 double dis(int x,int y)//算距离
 {
     return sqrt((x[x]-x[y])*(x[x]-x[y])+(y[x]-y[y])*(y[x]-y[y]));
 }
 double f[<<maxn][maxn];//s表示一个集合转换成二进制数，一个n个点，所以最大为2^n
 int main()
 {cin>>n;
    for(int i=;i<n;i++)//0~n-1方便二进制
          cin>>x[i]>>y[i];
    for(int i=;i<(<<n);i++)
        for(int j=;j<n;j++)
           f[i][j]=1e+;
     f[][]=;//为了对应二进制，起点变为0
   for(int s=;i<(<<n);s++)//枚举全部可能的点的集合
     {for(int i=;i<n;i++)//枚举停留点,要注意is是否在s里面
       {if((s>>i)&)//判断也就是s的第i位是否是1
         {for(j=;j<n;j++)//枚举要走哪个点
           if(((s>>j)&)==)//j不能走过
             f[s|(<<j)][j]=min(f[s|(<<j)][j],f[s][i]+dis(i,j));
          //f的第一维就是把j放到s集合里。
         }
       }
     }
    //最后枚举所有可能停的点中最小的一个
    double ans=1e+;
    for(int i=;i<n;i++)
      ans=min(ans,f[(<<n)-][i]);//n个1组成的所有的数：2^n-1
   cout<<ans<<endl;
 }   

说点数据范围的事儿

n<=20(22):状压        n<=12:O(n!)    n<=32(50)直接放弃 （来自长者的建议）       n<=100:n^3(Floyd,区间)   n<=1000:O(n^2)        n<=10^5:数据结构   n<=10^6:O(n)                    n>10^6:O(1)/O(log n)

区间DP：

合并石子：有n堆石子，可以合并相邻两堆。合并代价是这两堆的数目之和。把n堆石头合并为一堆，求最小代价。

把相邻的两堆合为一堆：区间dp

区间dp形式：f[l][r]代表把第l堆石子到第r堆石子合并为一堆的最小代价，求f[1][n]

边界：f[i][i]=0

转移：因为最后一次合并，一定是把某堆和另一堆合并为一堆。合并时不改变原来石头的顺序，所以合并的那两堆一定对应某个分界线，如下图：

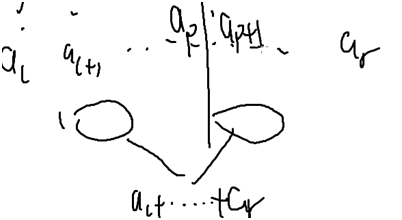
左边那一堆：f[l][p],右边那一堆：f[p+1][r].

so f[l][r]=min(f[l][p]+f[p+1][r]+sum[l][r])注意别忘加黄色部分。（区间和）这里我们枚举p）

 int f[][];
 int main()
 {int n,z[];
   cin>>n;
   for(int i=;i<=n;i++)
     cin>>z[i];
     make_sum();
   memset(f,0x3f,sizeof(f));//将f数组初始化为非常大的数 （最好不用0x7f,因为两个加起来爆int)
   for(int i=;i<=n;i++)
    f[i][i]=;//只有一堆：代价为0
    //我们需要枚举左端点，右端点，断点
    for(int l=;l<=n;l++)
      for(int r=l+;r<=n;r++)//r从l+1开始，因为r=l算完了
        for(int p=l;p<r;p++)
          f[l][r]=min(f[l][r],f[l][p]+f[p+][r]+sum[l][r]);//sum[l][r]用前缀和算一下
    //好了上面的那段是错的，但是为什么？
    //问题在于执行顺序。在算f[1][r]时f[2][r]，f[3][r]....都没有算过
    //每一个大区间都由两个小区间得来，所以我们在最外层枚举区间长度
        for(int len=;len<=n;len++)
          for(int l=;r=len;r<=n;l++,r++)//区间整体向右移动
            for(int p=l;p<r;p++)
              f[l][r]=min(f[l][r],f[l][p]+f[p+][r]+sum[l][r]);
    cout<<f[][n];
    //复杂度O(n^3),so n也就最多200多
 } 

如果我们把这n堆弄成个环，改怎么弄呢

a1,an 相邻处理方法：

ans=min(f[1][n],f[2][n+1])

但是a1,a2就不相邻了.....

考虑考虑，全部加完之后：

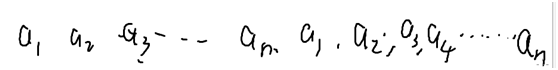
最终答案ans=min(f[i][n+i-1])

为什么呢？因为把一个环合成一个点，一定会有一条边用不到（合并相当于减少一条边）那我们把那条用不掉的边去掉。这里选择答案的过程就是枚举去掉哪条边

一些普通DP

我们用 f[i][j]:到第i行第j列的方案数

边界： f[1][j]=f[i][1]=1

转移：f[i][j]=f[i-1][j]+f[i][j-1];

小结论：左上角-->右下角

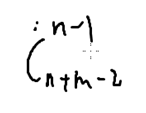
一共n+m-2步，向右走n-1步

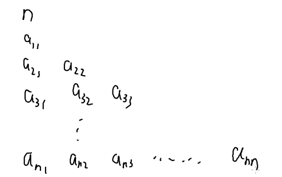
每次向下/右下走

权值：路径上所有数的和。要找权值最大的路径的值

f[i][j]:从(1,1)走到(i,j)的最大权值

f[1][1]=a[1][1]

f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j]从左上和正上走过来

改造版：

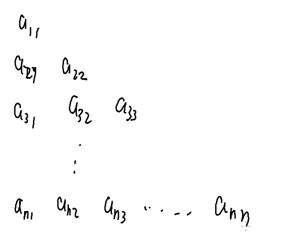
找到一条路径，使这条路的权值之和在模m之后最大

n,m<=100       数据比较x小---->给大了做不了/m也是个维度

（之前最优解不一定是之后最优解--->加维度）

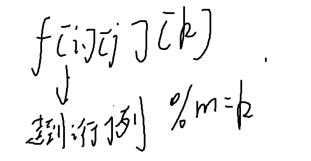
f[i][j][k]:

1,1到i,j 的权值和mod m=k是否可能存在

因为走到i,j之前的权值之和是k-aij,所以f[i][j][k]=f[i-1][j-1][(k-aij)mod m ] or f[i-1][j][k-aij]

边界:f[1][1][a11%m]=1

ans=最后一行最大的可能的k

f[i]表示以ai结尾的最长上升子序列的长度

枚举i前面的j<i,aj<ai,f[i]=max(f[j])+1

O(n^2)(T掉一半)

数据增强到10^5:用线段树。f[i]=max(f[j])+1(1<=j<i,aj<ai)

假设v=max(a1.........an)

建一棵长度为v的线段树

按值左右划分，所有f[i]<ai(对应的f)的数都在ai左边按照f[i]大小排序

轻松找出fj最大值，+1得到fi,然后修改，利用线段树进行区间询问最大值和单点修改

稍微特殊一点的DP：

背包：背包九讲qwq

01背包： 有n个物品，第i个的价值为wi，体积为vi.有一背包大小为m，在放入的物品体积之和不超过m的情况下，价值之和最大。这是最基本的问题。叫01背包是因为每个物品要么放进背包，要么不放进背包

f[i][j]表示判断完第1到i个物品，占用j体积的最大价值。

f[ i+1 ][ j ](第i+1个物品不放)=f[ i ][ j ]

f[ i+1 ][ j+v[ i+1 ] ](第i+1个物品放)=f[ i ][ j ]+w[ i+1 ]

完全（无穷）背包：有n个物品，第i个的价值为wi，体积为vi.有一背包大小为m，每种物品无数个，问最大权值。

把循环倒过来qwq

策略1：枚举每种用多少个   f[i][j]+x*w[i+1]àf[i+1][j+x*v[i+1]]

复杂度：

策略二：消掉枚举：f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i])

第i个物品选0个     又选了一次第i个物品

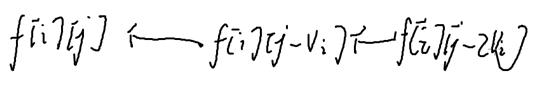
告诉每个物体有多少个：直接枚举

一些练习：

用数位DP。

显然要加一维

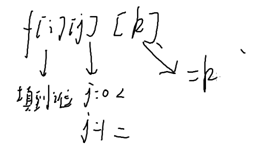
第三维记录乘积

但是k最大到9^18，总之空间会炸。

k不能为11（1~9的质因子只有2,3,5,7）

k可以写成如下形式：

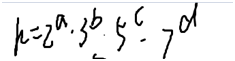
so，

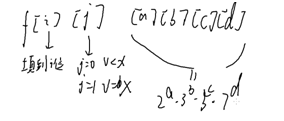
虽然它有6维，但它不会炸

因为a+b+c+d<=log210^18+log310^18+log510^18+log710^18