可持久化Treap 赛前摸鱼笔记
1.基本结构
随机化工具
unsigned int SEED = 19260817; //+1s
inline int Rand(){
SEED=SEED*1103515245+12345;
return SEED/65536;
}
内部成员
struct Treap{
int son[MAXN][2],val[MAXN],fix[MAXN],size[MAXN];
int tot,root;
#define lc son[o][0]
#define rc son[o][1]
}
初始化与构造
void init(){
root=0;//用于判断是否为NULL
tot=1; //所以tot从1遍历
son[0][0]=son[0][1]=val[0]=fix[0]=size[0]=0;
}
int node(int v){
son[tot][0]=son[tot][1]=0;
size[tot]=1;
val[tot]=v; //权值
fix[tot]=Rand(); //附加权值
return tot++;
}
void pu(int o){
size[o]=1+size[lc]+size[rc];
}
2.核心操作
void split(int o,int pivot,int &a,int &b){
if(!o){
a=b=0;
return;
}else if(val[o]<=pivot){ //如果节点权值小于等于pivot
a=o; //o所有左子树放到左边的树
split(rc,pivot,rc,b); //遍历右儿子
}else{
b=o;
split(lc,pivot,a,lc);
}
pu(o);
}
整体而言,这个操作就是把一个Treap分裂为左Treap和右Treap并把根节点分别赋给a b,其中左Treap所有权值总是小于等于pivot,右Treap则大于
并且这个操作复杂度为\(O(logn)\),下面简略说一下过程
来个小实验
int son[MAXN][2],val[MAXN];
#define lc son[o][0]
#define rc son[o][1]
void split(int o,int pivot,int &a,int &b){
if(!o){
a=b=0;
return;
}else if(val[o]<=pivot){
a=o;
split(rc,pivot,rc,b);
}else{
b=o;
split(lc,pivot,a,lc);
}
}
int main(){
val[1]=3,val[2]=2,val[3]=7;
val[4]=1,val[5]=5,val[6]=8;
val[7]=4,val[8]=6;
son[1][0]=2,son[1][1]=3;
son[2][0]=4;
son[3][0]=5,son[3][1]=6;
son[5][0]=7,son[5][1]=8;
int a,b;
split(1,5,a,b);
cout<<a<<" "<<b<<endl;
cout<<son[5][1]<<endl;
}
对方不想说话,并掏出了...沾满灰尘的破板子
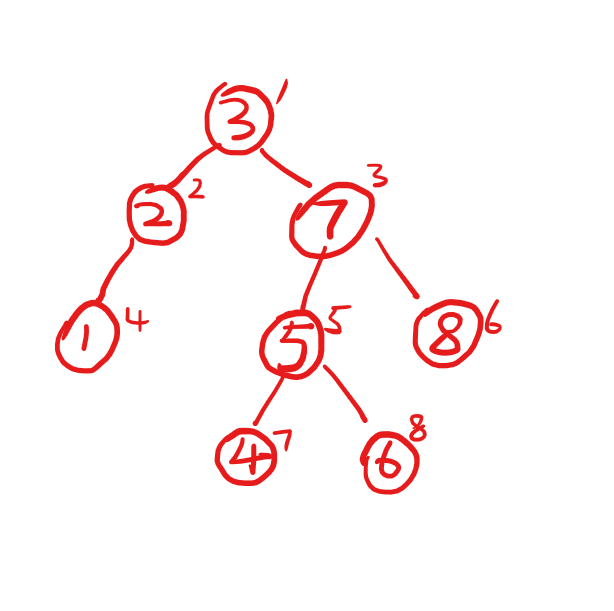
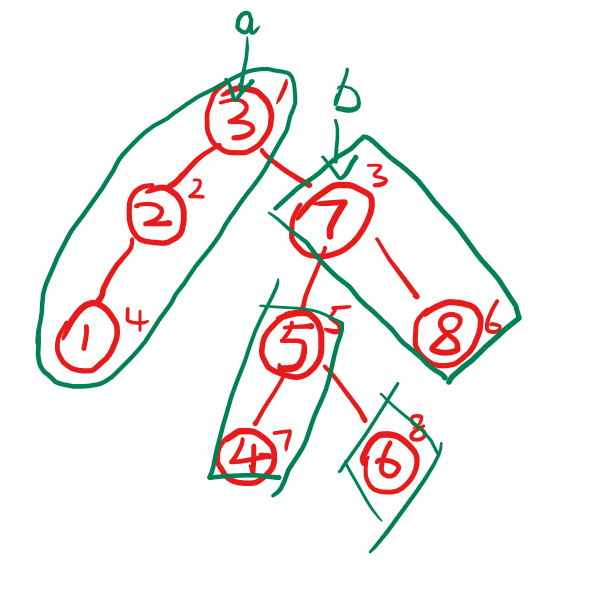
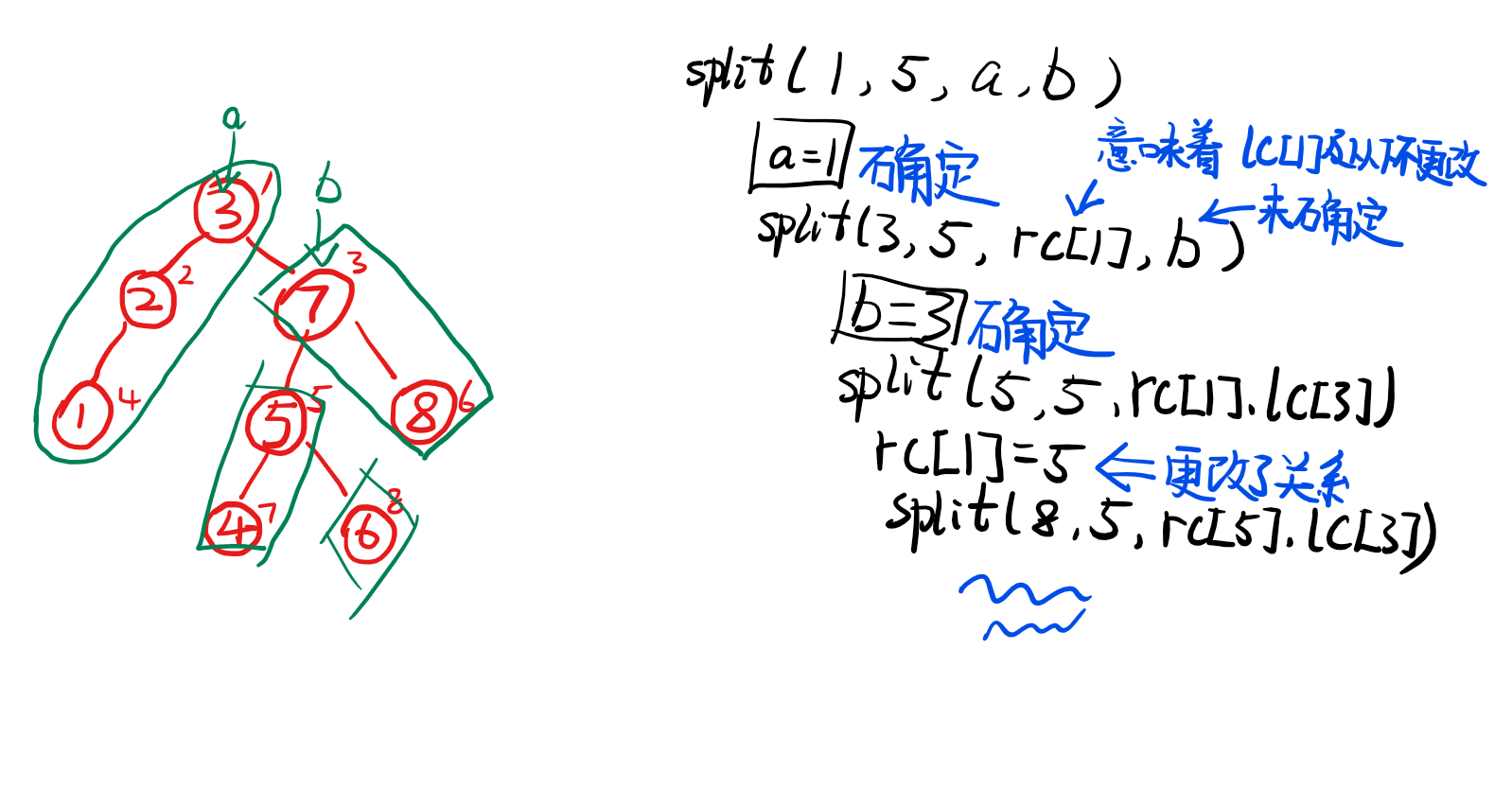
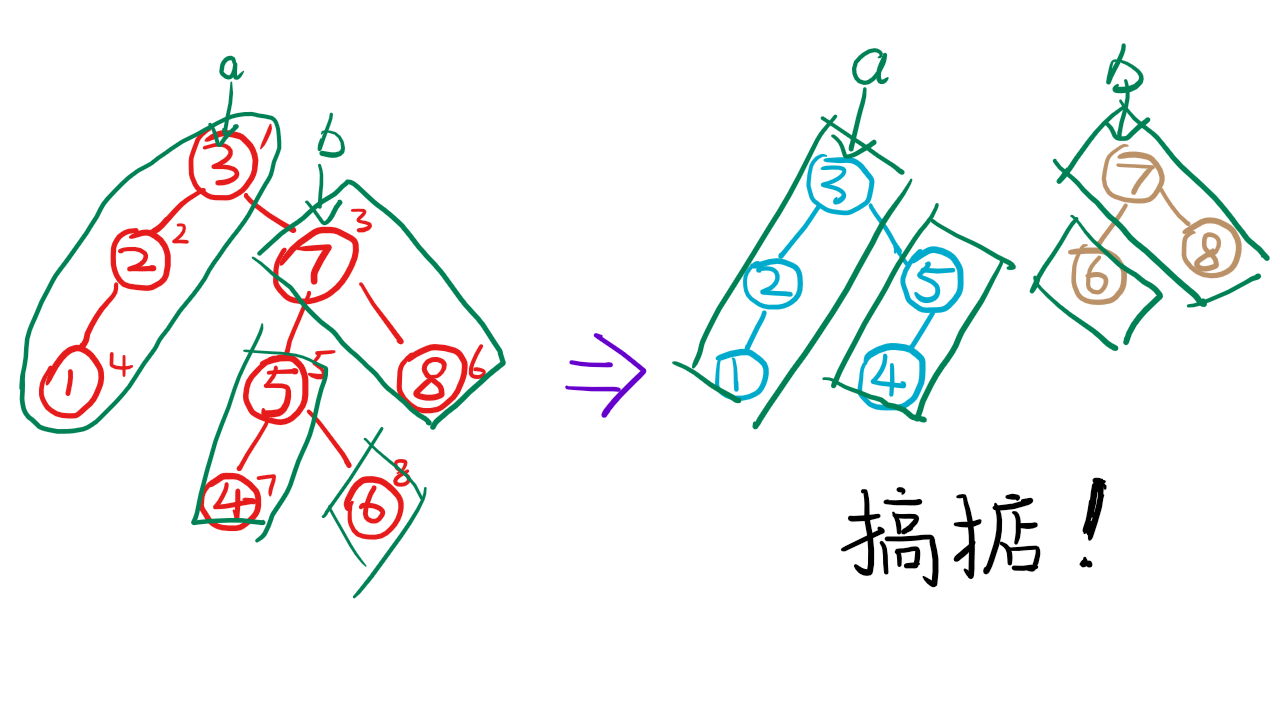
可以看出往左倾斜的方块放在a子树,往右倾斜的放在b子树,并且不断拼接就能分裂成完整的a和b
并且每一次操作就能把一半的子树摆好位置(随机fixed的情况下),所以整个操作流程就是\(O(logn)\)
一般使用还是按size划分比较好,提取区间简单轻松
void split(int o,int k,int &a,int &b){
if(!o){
a=b=0;
return;
}else if(k<=size[lc]){
b=o;
split(lc,k,a,lc);
pu(o);
}else{
a=o;
split(rc,k-size[lc]-1,rc,b);
pu(o);
}
}
int merge(int a,int b){ //保证val比较时a是左子树,b是右子树
if(!a) return b;
if(!b) return a;
if(fix[a]<fix[b]){
son[a][1]=merge(son[a][1],b);
pu(a);
return a; //a的左子树保留,(可能)更改右子树关系
}else{
son[b][0]=merge(a,son[b][0]);
pu(b);
return b;
}
}
merge是一个维护堆性质的过程,这个操作是十分的简单粗暴,再上一个小实验
int son[MAXN][2],fix[MAXN];
#define lc son[o][0]
#define rc son[o][1]
int merge(int a,int b){
if(!a)return a;if(!b)return b;
if(fix[a]<fix[b]){
son[a][1]=merge(son[a][1],b);
return a;
}else{
son[b][0]=merge(a,son[b][0]);
return b;
}
}
int main(){
fix[1]=10,fix[2]=20,fix[3]=30;
fix[4]=40,fix[5]=50,fix[6]=60;
fix[7]=80;
fix[8]=35,fix[9]=47,fix[10]=45;
fix[11]=75,fix[12]=65,fix[13]=55;
son[1][0]=2,son[1][1]=3;
son[2][0]=4;son[3][0]=5,son[3][1]=6;
son[4][0]=7;
son[8][0]=9,son[8][1]=10;
son[9][0]=11,son[9][1]=12;
son[10][1]=13;
merge(1,8);
for(int i=1;i<=12;i++){
cout<<i<<" "<<son[i][0]<<" "<<son[i][1]<<endl;
}
}
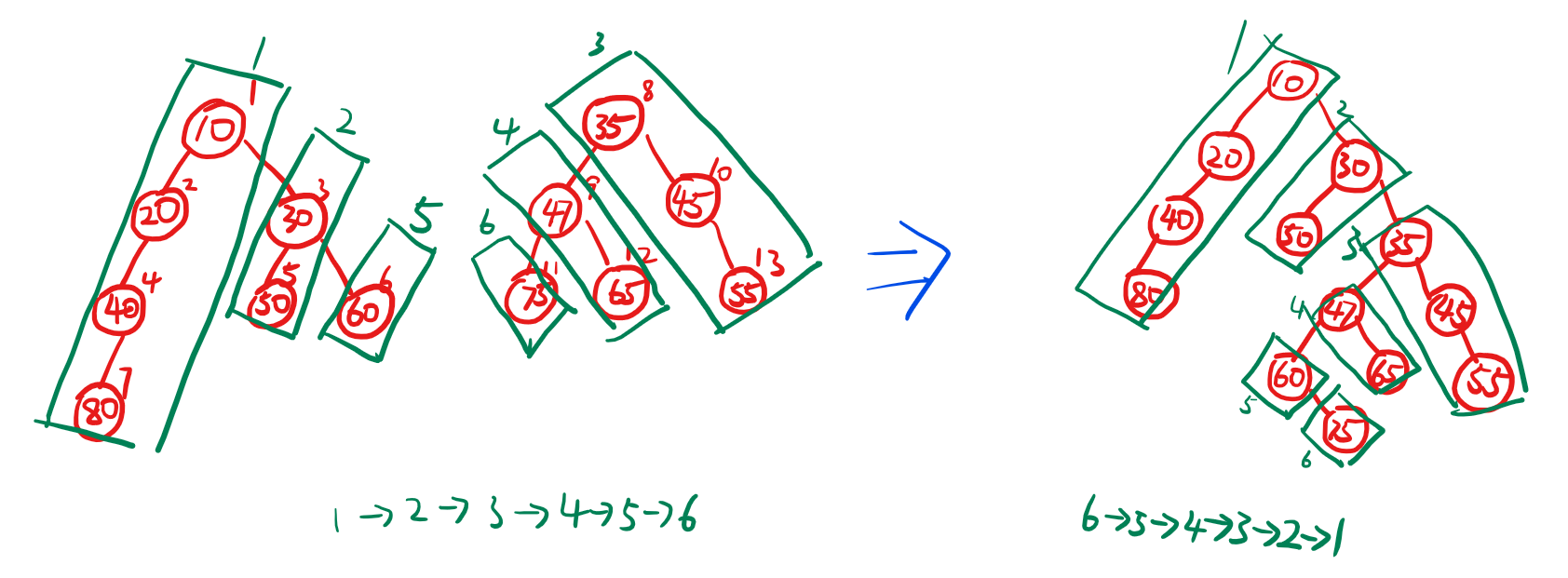
(这回画的更丑了)
可以看到其实还是一个分块再合并的过程,看着和斜堆很像,但更为暴力的是这家伙连左右交换都不做(当然它是有随机化buff加成可以为所欲为,而且还要维护val呢)
也就是说这个过程仅仅是通过维护一个堆的性质来合并而已,因为Rand()的存在令它依然是妥妥的\(O(logn)\)
按道理说想要降低常数那说还有一种策略就是把递归换成栈实现的迭代式,对频繁使用的核心操作而言应该是不小的提升,但递归写起来真方便..
3.区间操作
先来个最最简单插入/查询
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<string>
#include<vector>
#include<stack>
#include<queue>
#include<set>
#include<map>
#define rep(i,j,k) for(register int i=j;i<=k;i++)
#define rrep(i,j,k) for(register int i=j;i>=k;i--)
#define erep(i,u) for(register int i=head[u];~i;i=nxt[i])
#define iin(a) scanf("%d",&a)
#define lin(a) scanf("%lld",&a)
#define din(a) scanf("%lf",&a)
#define s0(a) scanf("%s",a)
#define s1(a) scanf("%s",a+1)
#define print(a) printf("%lld",(ll)a)
#define enter putchar('\n')
#define blank putchar(' ')
#define println(a) printf("%lld\n",(ll)a)
#define IOS ios::sync_with_stdio(0)
using namespace std;
const int MAXN = 1e5+11;
const int INF = 0x3f3f3f3f;
const double EPS = 1e-7;
typedef long long ll;
const ll MOD = 1e9+7;
unsigned int SEED = 17;
ll read(){
ll x=0,f=1;register char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline int Rand(){
SEED=SEED*1103515245+12345;
return SEED/65536;
}
struct Treap{
int son[MAXN][2],root,tot;
int val[MAXN],fix[MAXN],size[MAXN];
#define lc son[o][0]
#define rc son[o][1]
void init(){
root=0;
son[0][0]=son[0][1]=0;
val[0]=fix[0]=size[0]=0;
tot=1;
}
int node(int v){
son[tot][0]=son[tot][1]=0;
val[tot]=v; fix[tot]=Rand();
size[tot]=1;
return tot++;
}
void pu(int o){
size[o]=size[lc]+size[rc]+1;
}
void split(int o,int k,int &a,int &b){
if(!o){
a=b=0;
return;
}else if(k<=size[lc]){
b=o;
split(lc,k,a,lc);
pu(o);
}else{
a=o;
split(rc,k-size[lc]-1,rc,b);
pu(o);
}
}
int merge(int a,int b){
if(!a) return b;
if(!b) return a;
if(fix[a]<fix[b]){
son[a][1]=merge(son[a][1],b);
pu(a);
return a;
}else{
son[b][0]=merge(a,son[b][0]);
pu(b);
return b;
}
}
void insert(int pos,int v){
int a,b,t=node(v);
split(root,pos,a,b);
root=merge(merge(a,t),b);
}
int get(int k){
int a,b,x,y;
split(root,k-1,a,b);
split(b,1,x,y);
int t=x;
root=merge(a,merge(x,y));
return t;
}
}treap;
int n,m,a[MAXN];
int main(){
while(cin>>n>>m){
treap.init();
rep(i,1,n) a[i]=read();
rep(i,1,n){
treap.insert(i,a[i]);
}
rep(i,1,m){
int x; cin>>x;
int pos=treap.get(x);
cout<<treap.val[pos]<<endl;
}
}
return 0;
}
树形操作
BZOJ - 3224
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<string>
#include<vector>
#include<stack>
#include<queue>
#include<set>
#include<map>
#define rep(i,j,k) for(register int i=j;i<=k;i++)
#define rrep(i,j,k) for(register int i=j;i>=k;i--)
#define erep(i,u) for(register int i=head[u];~i;i=nxt[i])
#define iin(a) scanf("%d",&a)
#define lin(a) scanf("%lld",&a)
#define din(a) scanf("%lf",&a)
#define s0(a) scanf("%s",a)
#define s1(a) scanf("%s",a+1)
#define print(a) printf("%lld",(ll)a)
#define enter putchar('\n')
#define blank putchar(' ')
#define println(a) printf("%lld\n",(ll)a)
#define IOS ios::sync_with_stdio(0)
using namespace std;
const int MAXN = 2e5+11;
const int INF = 0x3f3f3f3f;
const double EPS = 1e-7;
typedef long long ll;
const ll MOD = 1e9+7;
unsigned int SEED = 19260817;
ll read(){
ll x=0,f=1;register char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline int Rand(){
SEED=SEED*1103515245+12345;
return SEED/65536;
}
struct Treap{
int son[MAXN][2],root,tot;
int val[MAXN],fix[MAXN],size[MAXN];
#define lc son[o][0]
#define rc son[o][1]
void init(){
root=0;
son[0][0]=son[0][1]=0;
val[0]=fix[0]=size[0]=0;
tot=1;
}
int node(int v){
son[tot][0]=son[tot][1]=0;
val[tot]=v; fix[tot]=Rand();
size[tot]=1;
return tot++;
}
void pu(int o){
size[o]=size[lc]+size[rc]+1;
}
void split(int o,int pivot,int &a,int &b){
if(!o){
a=b=0;
return;
}else if(val[o]>pivot){
b=o;
split(lc,pivot,a,lc);
pu(o);
}else{
a=o;
split(rc,pivot,rc,b);
pu(o);
}
}
int merge(int a,int b){
if(!a) return b;
if(!b) return a;
if(fix[a]<fix[b]){
son[a][1]=merge(son[a][1],b);
pu(a);
return a;
}else{
son[b][0]=merge(a,son[b][0]);
pu(b);
return b;
}
}
void insert(int v){
int a,b,t=node(v);
split(root,v,a,b);
root=merge(merge(a,t),b);
}
void del(int x){
int a,b,c,d;
split(root,x,a,b);
split(a,x-1,c,d);
d=merge(son[d][0],son[d][1]);//d的根不要了
root=merge(merge(c,d),b);
}
int krank(int k){
int a,b;
split(root,k-1,a,b);
int res=size[a]+1; //最小的相同数必然是恰比k-1子树规模大
root=merge(a,b);
return res;
}
int kth(int k){
int o=root;
while(1){
if(k<=size[lc]){
o=lc;
}else if(k==size[lc]+1){
return o;
}else{
k-=size[lc]+1;
o=rc;
}
}
}
int kth(int o,int k){
while(1){
if(k<=size[lc]){
o=lc;
}else if(k==size[lc]+1){
return o;
}else{
k-=size[lc]+1;
o=rc;
}
}
}
int pre(int x){
int a,b;
split(root,x-1,a,b);
int t=kth(a,size[a]);
root=merge(a,b);
return t;
}
int succ(int x){
int a,b;
split(root,x,a,b);
int t=kth(b,1);
root=merge(a,b);
return t;
}
}tp;
int n,m,a[MAXN];
int main(){
while(cin>>n){
tp.init();
rep(i,1,n){
int op=read();
int x=read();
switch(op){
case 1:tp.insert(x);break;
case 2:tp.del(x);break;
case 3:println(tp.krank(x));break;
case 4:println(tp.val[tp.kth(x)]);break;
case 5:println(tp.val[tp.pre(x)]);break;
case 6:println(tp.val[tp.succ(x)]);break;
}
}
}
return 0;
}
区间操作+简单标记
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<string>
#include<vector>
#include<stack>
#include<queue>
#include<set>
#include<map>
#define rep(i,j,k) for(register int i=j;i<=k;i++)
#define rrep(i,j,k) for(register int i=j;i>=k;i--)
#define erep(i,u) for(register int i=head[u];~i;i=nxt[i])
#define iin(a) scanf("%d",&a)
#define lin(a) scanf("%lld",&a)
#define din(a) scanf("%lf",&a)
#define s0(a) scanf("%s",a)
#define s1(a) scanf("%s",a+1)
#define print(a) printf("%lld",(ll)a)
#define enter putchar('\n')
#define blank putchar(' ')
#define println(a) printf("%lld\n",(ll)a)
#define IOS ios::sync_with_stdio(0)
using namespace std;
const int MAXN = 2e5+11;
const double EPS = 1e-7;
typedef long long ll;
const ll MOD = 1e9+7;
unsigned int SEED = 19260817;
const ll INF = 1ll<<60;
ll read(){
ll x=0,f=1;register char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline int Rand(){
SEED=SEED*1103515245+12345;
return SEED/65536;
}
struct Treap{
int son[MAXN][2],root,tot;
int val[MAXN],fix[MAXN],size[MAXN];
ll mx[MAXN];
#define lc son[o][0]
#define rc son[o][1]
void init(){
root=0;
son[0][0]=son[0][1]=0;
val[0]=fix[0]=size[0]=0;
mx[0]=-INF;
tot=1;
}
int node(int v){
son[tot][0]=son[tot][1]=0;
val[tot]=v; fix[tot]=Rand();
size[tot]=1;mx[tot]=v;
return tot++;
}
void pu(int o){
size[o]=size[lc]+size[rc]+1;
mx[o]=max((ll)val[o],mx[lc]);
mx[o]=max(mx[o],mx[rc]);
}
void split(int o,int k,int &a,int &b){
if(!o){
a=b=0;
return;
}else if(k<=size[lc]){
b=o;
split(lc,k,a,lc);
pu(o);
}else{
a=o;
split(rc,k-size[lc]-1,rc,b);
pu(o);
}
}
int merge(int a,int b){
if(!a) return b;
if(!b) return a;
if(fix[a]<fix[b]){
son[a][1]=merge(son[a][1],b);
pu(a);
return a;
}else{
son[b][0]=merge(a,son[b][0]);
pu(b);
return b;
}
}
void insert(int pos,int v){
int a,b,t=node(v);
split(root,pos,a,b);
root=merge(merge(a,t),b);
}
}tp;
int main(){
int n;
while(cin>>n){
tp.init();
rep(i,1,n){
int x,y;
cin>>x>>y;
tp.insert(x,y);
}
rep(i,1,n){
int a,b,x,y;
tp.split(tp.root,i-1,a,b);
tp.split(b,3,x,y);//[i,i+2]的最大值
// cout<<tp.val[x]<<" "<< //此时val已经无意义
cout<<tp.mx[x]<<endl;
tp.root=tp.merge(a,tp.merge(x,y));
}
}
return 0;
}
//如果插入i区间表示原来i后面插入
可持久化Treap 赛前摸鱼笔记的更多相关文章
- 【FCS NOI2018】福建省冬摸鱼笔记 day3
第三天. 计算几何,讲师:叶芃(péng). dalao们日常不记笔记.@ghostfly233说他都知道了,就盼着自适应辛普森积分. 我计算几何基础不好……然而还是没怎么讲实现,感觉没听什么东西进去 ...
- 【FCS NOI2018】福建省冬摸鱼笔记 day2
第二天. 同学还是不带本子记笔记.dalao. 第二天:图论,讲师:@ExfJoe 全程划水,前面都讲水算法[虽然我可能已经忘记了]什么最短路,Tarjan,最小生成树,2SAT,差分约束啥的,我现在 ...
- 【FCS NOI2018】福建省冬摸鱼笔记 day1
省冬的第一天. 带了本子,笔,一本<算法导论>就去了.惊讶于为什么同学不带本子记笔记. 他们说:“都学过了.”,果然这才是巨神吧. 第一天:数论,讲师:zzx 前几页的课件挺水,瞎记了点笔 ...
- Hash 日常摸鱼笔记
本篇文章是Hash在信息学竞赛中的应用的学习笔记,分多次更新(已经有很多坑了) 一维递推 首先是Rabin-Karp,对于一个长度为\(m\)的串\(S\) \(f(S)=\sum_{i=1}^{m} ...
- 【FCS NOI2018】福建省冬摸鱼笔记 day6【FJOI 2018】福建省选混分滚蛋记 day1
记录一下day6发生的事情吧. 7:30 到达附中求索碑,被人膜,掉RP. 7:50 进考场,6楼的最后一排的最左边的位置,世界上最角落的地方,没有任何想法. 发现电脑时间和别人不一样,赶快调了一下. ...
- 【FCS NOI2018】福建省冬摸鱼笔记 day5
第五天,也是讲课的最后一天. 数据结构专题,讲师:杨志灿 他的blog我似乎找不到了……以前肯定是在百度博客里面.但是现在百度博客消失了. PPT做的很有感觉,说了很多实用的技巧. 我觉得其实是收获最 ...
- 【FCS NOI2018】福建省冬摸鱼笔记 day4
第四天. 动态规划专题,讲师:闫神 讲了一些DP优化技巧,然而思想难度好大啊……根本没想到能优化那地步,连DP方程都没有呢. 不过有几题我还是想明白了. 讲了单调队列,决策单调性,四边形不等式,斜率优 ...
- [摸鱼]cdq分治 && 学习笔记
待我玩会游戏整理下思绪(分明是想摸鱼 cdq分治是一种用于降维和处理对不同子区间有贡献的离线分治算法 对于常见的操作查询题目而言,时间总是有序的,而cdq分治则是耗费\(O(logq)\)的代价使动态 ...
- 【转】让Chrome化身成为摸鱼神器,利用Chorme运行布卡漫画以及其他安卓APK应用教程
下周就是十一了,无论是学生党还是工作党,大家的大概都会有点心不在焉,为了让大家更好的心不在焉,更好的在十一前最后一周愉快的摸鱼,今天就写一个如何让Chrome(google浏览器)运行安卓APK应用的 ...
随机推荐
- postfix配置积累(不断的积累)
postfix 配置 1.mail_name 默认是Postfix.在收件人信头可以查看,如果不想让别人知道你是用postfix发的,则可以改成其它名字,如:postconf -e mail_name ...
- 4.SELECT DISTINCT 语句
在表中,可能会包含重复值.这并不成问题,不过,有时您也许希望仅仅列出不同(distinct)的值. 关键词 DISTINCT 用于返回唯一不同的值. 语法: SELECT DISTINCT 列名称 F ...
- ifcfg-eth0文件参数PREFIX 和 NETMASK的配置不一致问题
ifcfg-eth0文件参数PREFIX 和 NETMASK的配置不一致问题 摘自:https://blog.csdn.net/aikui0621/article/details/9148997 阅读 ...
- 第十九课 pluginlib&Nodelet
把rgb摄像头的数据转换为laser的时候使用了Nodelet. pluginlib(插件库) 在ros中有一个plugin的包,下面是一个ROS Plugin Registration的例子 上面包 ...
- 编写高质量代码改善C#程序的157个建议——建议31:在LINQ查询中避免不必要的迭代
建议31:在LINQ查询中避免不必要的迭代 无论是SQL查询还是LINQ查询,搜索到结果立刻返回总比搜索完所有的结果再将结果返回的效率要高. 示例代码: class MyList : IEnumera ...
- JQuery.validator插件使用
首先给变量validator赋值 var validator =$('#test').validate({validate构造 }); 接着调用 $('#test').valid() 会使用上面的验证 ...
- ORACLE_ERP帐务分录
ORACLE MRPII各模块会计分录 第一章 采购模块 一.资产采购(科目来源:库存组织) 1.物料接收 借 材料采购 接收数量*采购单价 贷 应计暂估 接收数量*采购单价 ...
- asp.net站点阻止某个文件夹或者文件被浏览器访问
一个站点根目录下面有一个Config文件夹,这个文件夹里面都是一些json格式的txt文本,文本是一种静态资源,如果知道这个文本的地址,就可以在浏览器中输入地址打开这个文本,别人就可以看到站点的配置, ...
- 我的java问题排查工具单
前言 平时的工作中经常碰到很多疑难问题的处理,在解决问题的同时,有一些工具起到了相当大的作用,在此书写下来,一是作为笔记,可以让自己后续忘记了可快速翻阅,二是分享,希望看到此文的同学们可以拿出自己日常 ...
- 性能测试常用sql语句
做了一段时间的性能测试,把自己在性能测试过程中,使用到的Oracle中用到的sql语句整理一番,做个备忘: (1)多个字段以某种格式拼接 Oracle方式:"||"字符串拼接符; ...
