FFT快速傅立叶变换：解析wav波频图、Time Domain、Frequency Domain
您好，此教程将教大家使用scipy.fft分析wav文件的波频图、Time Domain、Frequency Domain。
实际案例：声音降噪，去除高频。
结果：
波频图：
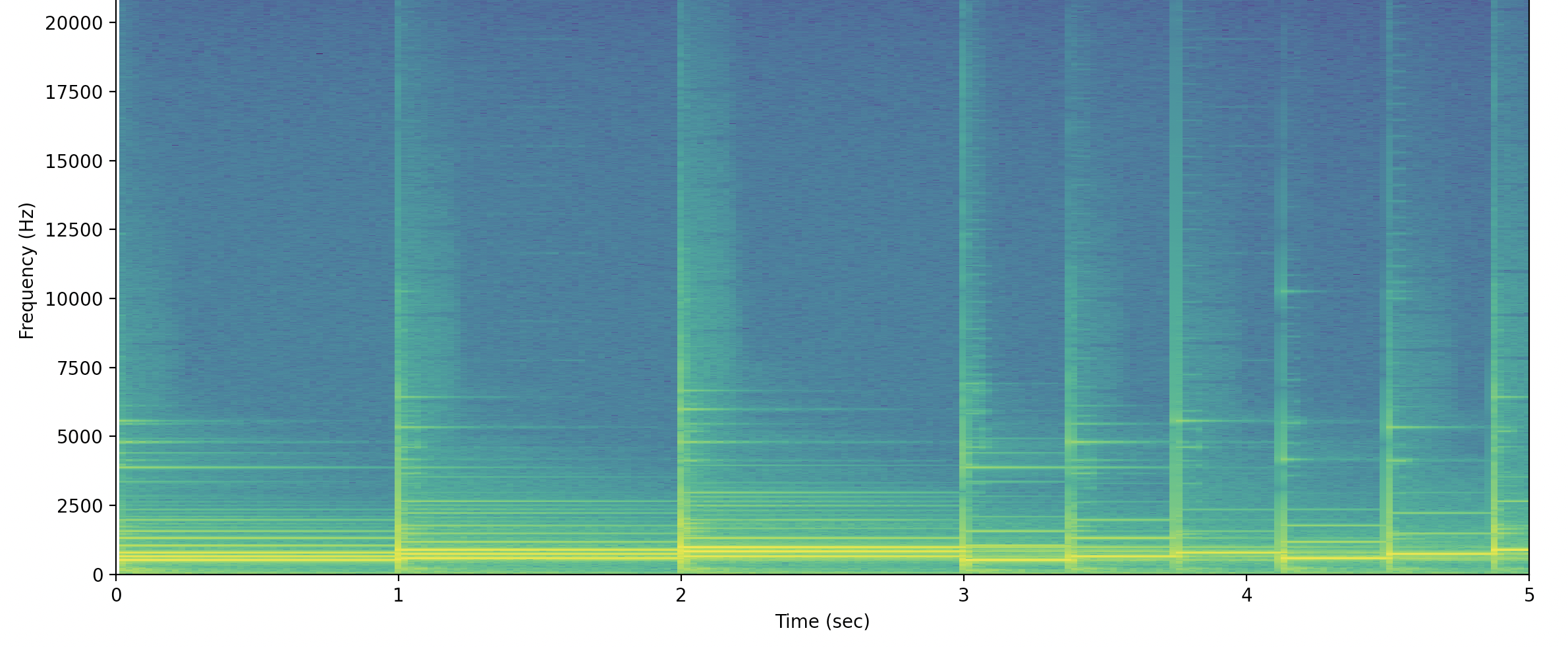
Time Domain：
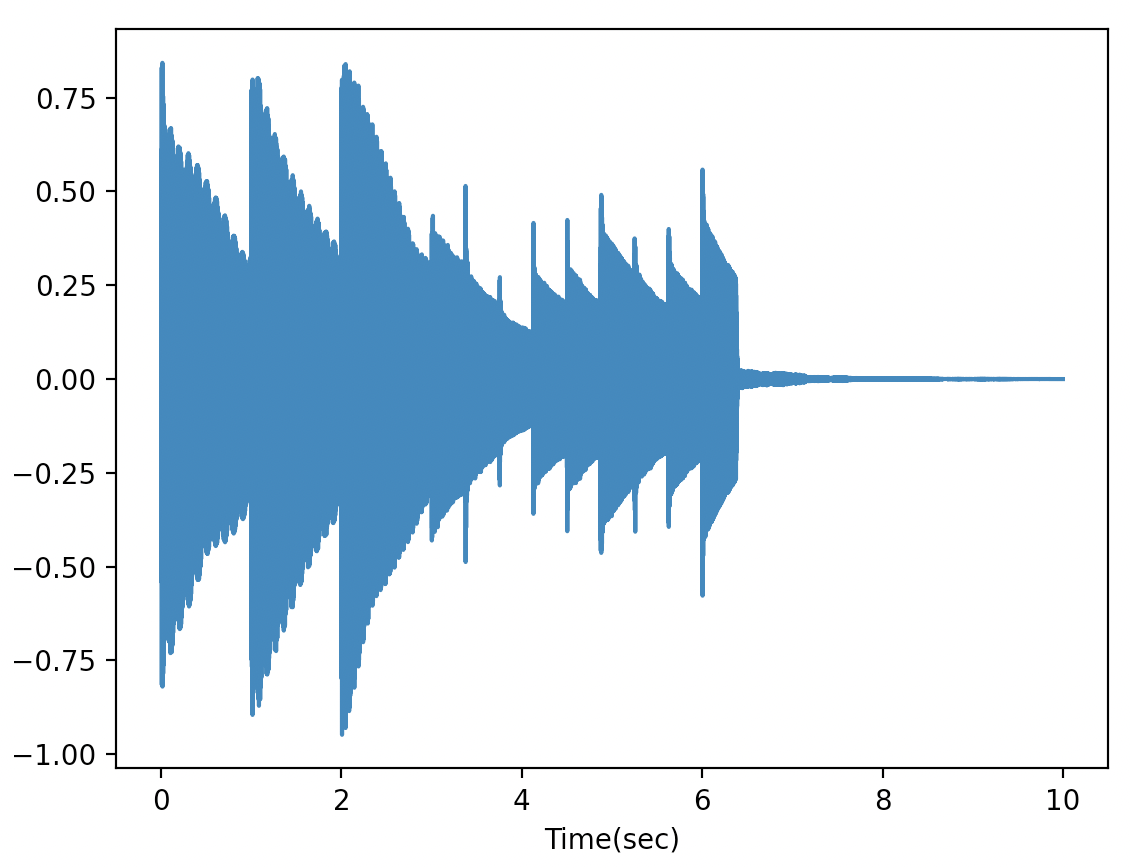
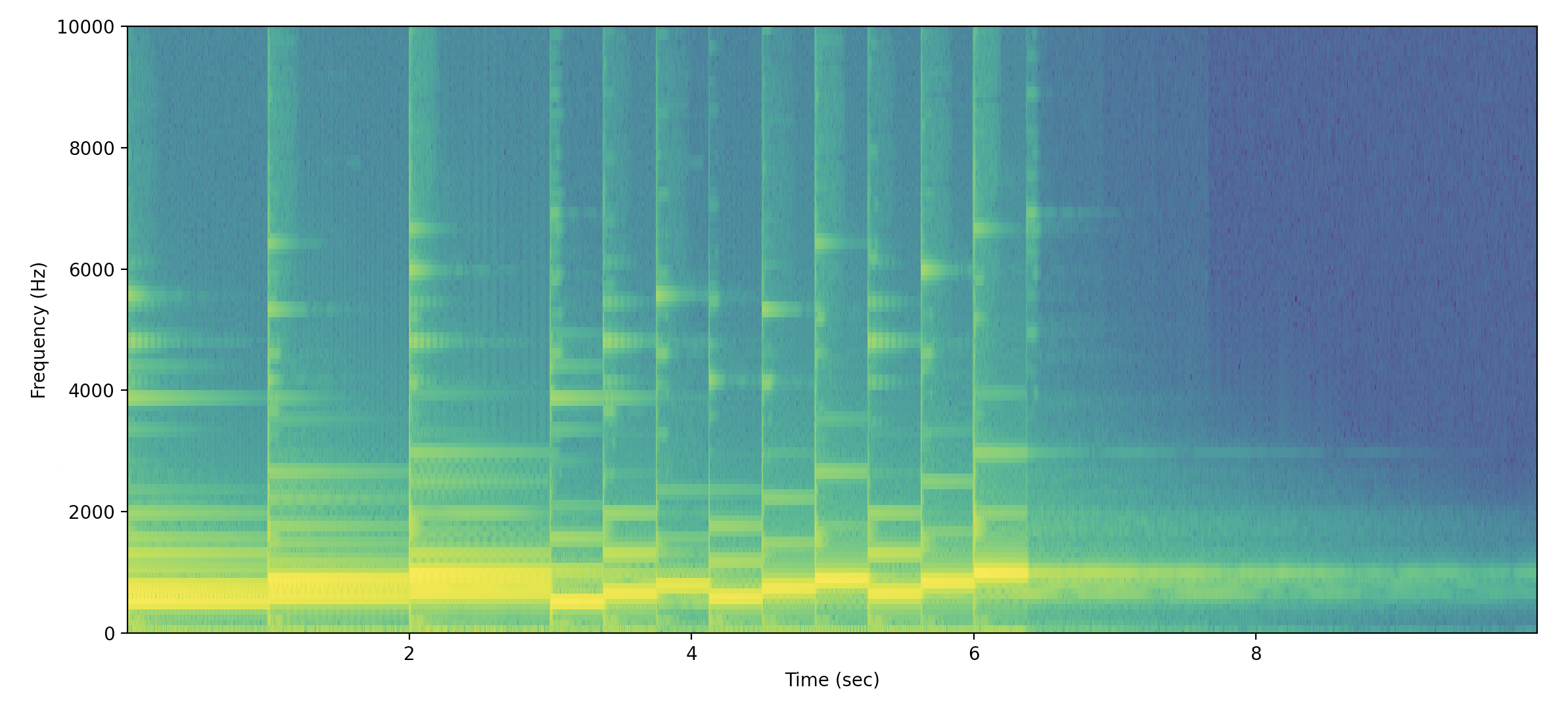
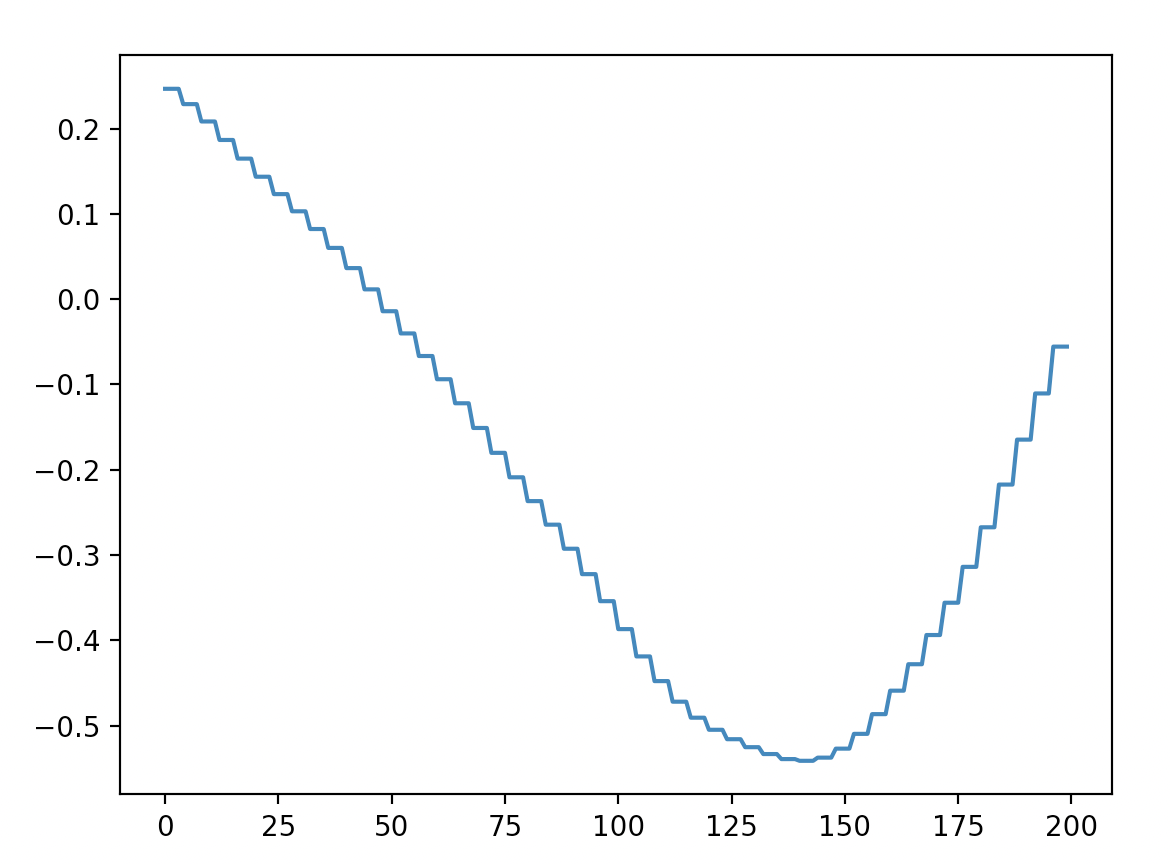
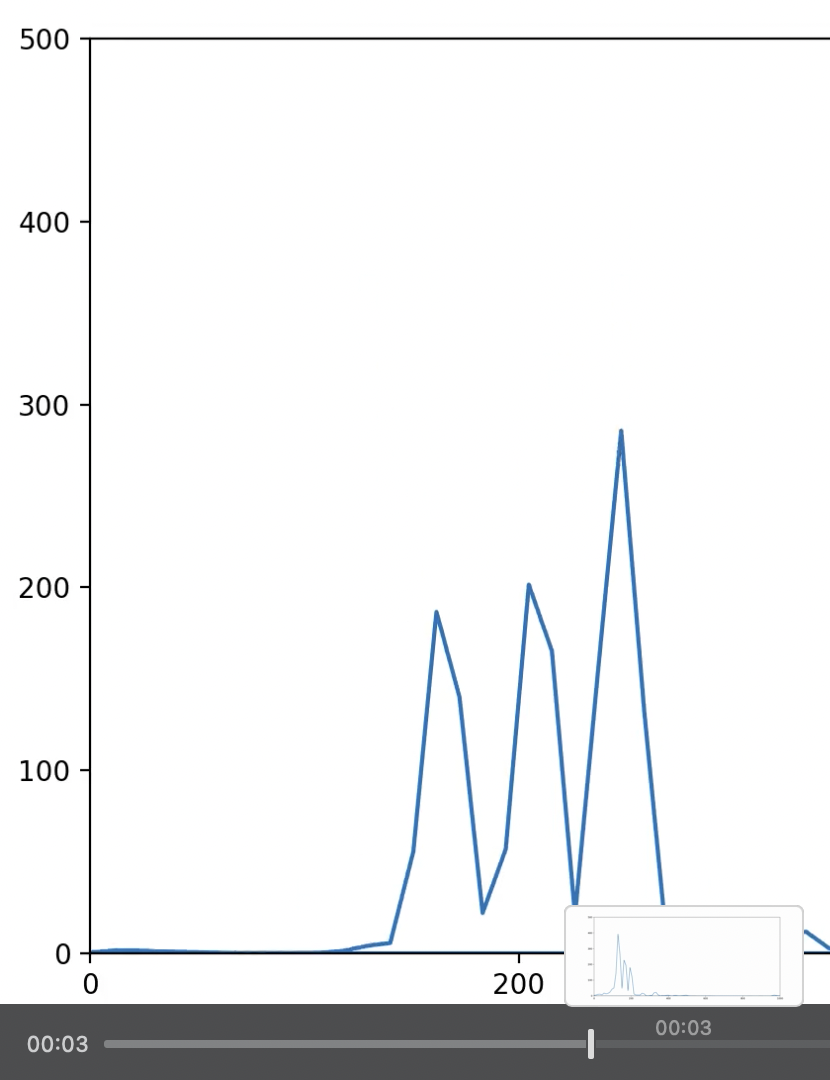
FFT快速傅立叶变换：解析wav波频图、Time Domain、Frequency Domain的更多相关文章
- FFT快速傅立叶变换的工作原理
实数DFT,复数DFT,FFTFFT是计算DFT的快速算法,但是它是基于复数的,所以计算实数DFT的时候需要将其转换为复数的格式,下图展示了实数DFT和虚数DFT的情况,实数DFT将时域中N点信号转换 ...
- spoj VFMUL FFT快速傅立叶变换模板题
题意:求两个数相乘. 第一次写非递归的fft,因为一个数组开小了调了两天TAT. #include<iostream> #include<cstring> #include&l ...
- FFT(快速傅立叶变换)：HDU 1402 A * B Problem Plus
Calculate A * B. Input Each line will contain two integers A and B. Process to end of file. Note: th ...
- FFT快速傅立叶变换
//最近突然发现博客园支持\(\rm\LaTeX\),非常高兴啊! 话说离省选只有不到五天了还在学新东西确实有点逗…… 切到正题,FFT还是非常神奇的一个东西,能够反直觉地把两个多项式相乘的时间复杂度 ...
- 离散傅立叶变换与快速傅立叶变换（DFT与FFT）
自从去年下半年接触三维重构以来,听得最多的词就是傅立叶变换,后来了解到这个变换在图像处理里面也是重点中的重点. 本身自己基于高数知识的理解是傅立叶变换是将一个函数变为一堆正余弦函数的和的变换.而图像处 ...
- 快速傅立叶变换(FFT)算法
已知多项式f(x)=a0+a1x+a2x2+...+am-1xm-1, g(x)=b0+b1x+b2x2+...+bn-1xn-1.利用卷积的蛮力算法,得到h(x)=f(x)g(x),这一过程的时间复 ...
- $\mathcal{FFT}$·$\mathcal{Fast \ \ Fourier \ \ Transformation}$快速傅立叶变换
\(2019.2.18upd:\) \(LINK\) 之前写的比较适合未接触FFT的人阅读--但是有几个地方出了错,大家可以找一下233 啊-本来觉得这是个比较良心的算法没想到这么抽搐这个算法真是将一 ...
- BZOJ 2194 快速傅立叶变换之二 | FFT
BZOJ 2194 快速傅立叶变换之二 题意 给出两个长为\(n\)的数组\(a\)和\(b\),\(c_k = \sum_{i = k}^{n - 1} a[i] * b[i - k]\). 题解 ...
- 快速傅立叶变换（FFT）
多项式 系数表示法 设\(f(x)\)为一个\(n-1\)次多项式,则 \(f(x)=\sum\limits_{i=0}^{n-1}a_i*x_i\) 其中\(a_i\)为\(f(x)\)的系数,用这 ...
随机推荐
- 将 Ubuntu 16.04 LTS 的 Unity 启动器移动到桌面底部命令
将 Ubuntu 16.04 LTS 的 Unity 启动器移动到桌面底部命令: gsettings set com.canonical.Unity.Launcher launcher-positio ...
- 【Java面试】Mysql为什么使用B+Tree作为索引结构
一个工作8年的粉丝私信了我一个问题. 他说这个问题是去阿里面试的时候被问到的,自己查了很多资料也没搞明白,希望我帮他解答. 问题是: "Mysql为什么使用B+Tree作为索引结构" ...
- vmware修改虚拟机网卡mac地址
选中"虚拟机" 右键 "设置",然后选中"网络适配器",然后点击"高级",设置"MAC地址"
- 华为HMS Core携手超图为三维GIS注入新动能
6月30日,在2022(第五届)GIS软件技术大会GIS基础软件新技术板块论坛上,华为联合超图推出了基于HMS Core 3D Engine开发的高保真三维GIS插件,通过3D渲染技术助力三维GIS实 ...
- Day04 HTML标记
路径 ./ 同级目录 ./ 进入该目录名下 ../ 上一级目录 HTML标记 图片 <!-- 图片标记 src 图片的路径 width 设置图片宽度 height 设置图片高度 title 鼠标 ...
- Apache：dbutils 开源JDBC工具类库
commons-dbutils jar:下载 package com.jdbc.tools; import org.apache.commons.dbutils.QueryRunner; import ...
- spingboot打jar包
pom.xml文件中packaging为jar <packaging>jar</packaging> 安装插件 <plugin> <groupId>or ...
- MISC 2022/4/21 刷题记录-千字文
1.千字文 得到名为png的无类型文件,010 Editor查看,png,改后缀,得到二维码 QR扫描,得到一句话"这里只有二维码" 思路不对,binwalk一下,发现有错误信息 ...
- DDS信号发生器加强版（双通道，发送波形的频率可控，相位可控，种类可控）
目的:设计一个DDS,可以输出两个波形,输出的波形的周期可以修改,相位可以修改,种类也可以修改 输入:clk,reset,一个控制T的按键,一个控制相位的按键,一个控制波形种类的按键. 思路:双通道- ...
- K阶斐波那契数列--------西工大NOJ习题.10
K阶斐波那契数列--------西工大NOJ习题.10 原创不易,转载请说明出处!!! 科普:k阶斐波那契数列的0到n-1项需要有初始值. 其中,0到n-2项初始化为0,第n-1项初始化为1. 在这道 ...